学生逻辑推理能力的重要性及培养方法

根据笔者多年的教学经验，结合教学实践，学生要具备较强的推理能力需要具备以下方面的能力：牢固的数学基础知识、必要的逻辑知识、提出猜想的能力、灵活运用各种证明技巧的能力。

（一）牢固的数学基础知识

数学基础知识是指数学中的概念、定理和公式，这些是数学学习的核心部分，也是进行逻辑推理论证的依据。学生只有在熟练掌握这些内容的基础上，才能逐步形成推理论证能力。

概念是人们脑海中对于客观事物本质的反映，是学习数学的“基石”，是进行判断、推理的基础。在教授概念时，教师一定要讲透它，通过深挖和外延数学概念帮助学生掌握事物的本质，否则就会出现概念模糊，进而导致思维出现混乱。因此，只有在理解、掌握概念的基础上，学生才能进行正确的判断和推理。

数学的公式和定理则是进行推理论证的依据，这些内容都是以往科学家经过严格逻辑推理所得到的，如果没有正确的依据，就难以对所要证明的命题进行正确的分析、推导，也就不能进行正确的论证。因此，教师担负着讲清楚公式、定理的重任，要使学生都能牢记数学内容，还可以运用已知的条件来进行推导，最后通过观察、推理来得到正确的结论。

（二）必要的逻辑知识

数学不同于其他学科的最主要的一点就是严密的逻辑性，甚至于“1+1=2”都需要有严谨的论证过程。在数学的计算过程中，一切的推理过程都离不开逻辑。由于许多学生掌握的逻辑知识较少，这就导致在论证的过程中会出现一些错误，如强加一些额外条件、无根据的推理、将猜想作为事实等，从而导致论证过程的失败。因此，在授课时，教师不妨穿插渗透讲述一些逻辑思维，帮助学生在潜移默化中提升自身的逻辑推导能力。

（三）提出猜想的能力

数学猜想是证明数学命题之前的一个思维的过程。在详细证明之前，脑海中必须要先通过猜想来得到证明的思路，将结果与思路进行综合比较，进行一次次尝试后，最后得到正确的答案。比如，著名的哥德巴赫猜想、四色猜想等，都是伟大的数学家所做出的贡献。现在，依然有一些猜想未被攻克，这吸引着无数的数学家进行研究、证明，成为数学向前发展的巨大动力。在高中教学中，教师可以创设一些课堂情境，激发学生的兴趣，使他们能够进行猜想，培养他们大胆猜想的习惯，然后再点评猜想的内容是否合理。

数学猜想的方法一般有归纳概括法、类比猜想这两种思路。

归纳概括方法是学生在学习中经常用到的方法，主要应用于科学发现的过程，在数学史中也是如此，如勾股定理、哥德巴赫猜想等著名定理。伟大的数学家高斯也说过他的许多定理都是通过归纳方法得到的。在数学教材中，等差、等比数列的通项公式就是通过归纳的方法得到的。在高考试卷中，归纳猜想在数列证明中常常用到。下面就是一道归纳概括的证明题：

例题：（2012年广东数学卷）设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1+1，n∈N+，且a1，a2+5，a3成等差数列。

①求a1的值。

②求数列{an}的通项公式。

③证明：对于一切正整数n，有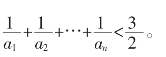

解析：

①在2Sn=an+1-2n+1+1中，令n=1，得2S1=a2-22+1，即a2=2a1+3；(www.xing528.com)

令n=2，得2S2=a3-23+1，即a3=6a1+13；

又有2（a2+5）=a1+a3。

联立上述三式，得a1=1。

②由2Sn=an+1-2n+1+1得2Sn+1=an+2-2n+2+1，将两式进行作差，得an+2=3an+1+2n+1，

又有a1=1，a2=5，满足a2=3a1+21，

∴an+1=3an+2n对于n∈N+成立。

∴an+1+2n+1=3（an+2）n，∴an+2n=3n，即an=3n-2n。

③因为an+1=3n+1-2n+1﹥2×3n-2n+1=2an，所以

所以当n≥2时，得

两边同时相乘得

所以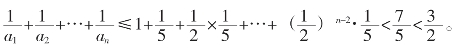

上述类型的试题在各地高考试卷中几乎年年都会出现，这也从侧面说明数学归纳概括类型的试题在高考中很受命题者的青睐。因此，教师需要重视讲授这种类型的试题。

类比思想是指运用类比的方法，通过两个对象或者问题之间存在的相似性来将信息从一个对象转移到另一个对象，从而实现知识的迁移。在研究问题的过程中，研究者经常在某一问题上陷入沉思，找不到突破的方向，如果进行某种类比，就有可能出现“柳暗花明又一村”的惊喜，最终顺利地解决问题。在数学学习过程中，也存在这样的道理，教师要培养学生的类比思想。

（四）灵活运用各种证明技巧的能力

证明的过程就是通过“已知”来推导得到“结论”，要想在“已知”和“结论”之间建立联系，就需要进行数学的思维。在解题的过程中，学生需要从已知条件出发，经过全方位、多角度思考来寻求结论的可能性，找到解决问题的设想和方法，从而抓住问题的本质，顺利地对问题进行求解。