像素级变化检测方法在城市遥感中的应用

像素级变化检测方法以影像内像素为分析单元，通过特定方法如影像差分、影像回归、像素比值等提取影像像素灰度值的变化信息，一般不顾及像素之间的关系。

1.差值法

影像差值法对多时相影像中对应像素的灰度值进行相减，结果影像代表了两个时间影像的变化。表达式如式(14-1)所示。影像差值法可以应用于单一波段(称作单变量影像差分)，也可以应用于多波段(称作多变量影像差分)。

式中，i、j为像素坐标值；k为波段；t1、t2为第一幅影像时间、第二幅影像时间；C为常量，用来得到正值。

由于最后只要找到变化的区域，为此更改影像差值公式(14-1)为公式(14-2)。

对差值影像进行统计处理，计算差值影像的均值和标准差。如果差值影像中像素的灰度值满足公式(14-3)，就认为该像素发生变化。

式中，m为差值影像均值；STD为差值影像标准差；Td为门限值。

用对应像素灰度值直接相减的效果很差，一般都取窗口，用窗口均值代替窗口中心像素的灰度值进行计算。

2.相关系数法

相关系数法计算多时相影像中对应像素灰度的相关系数，结果代表了两个时间影像中对应像素的相关性。一般是取窗口，计算两个影像中对应窗口的相关系数，以表示窗口中心像素的相关性。如果相关系数值接近1，则说明相关性很高，该像素没有变化；反之，则说明该像素发生了变化。通过公式(14-4)得到相关系数，如果相关系数r满足公式(14-5)，就认为该像素发生变化，Tr为门限值。

3.比值法

比值法通过计算已配准的多时相影像对应像素的灰度值的比值来完成变化检测分析。如果在一个像素上没有发生变化，则比值接近1，如果在此像素上发生变化，则比值远大于或远小于1(依靠变化的方向)。数学表达式如公式(14-6)所示。

式中，Tl和Th分别代表低门限和高门限。

4.影像回归法

通过选择合适的阈值，可以确定变化的区域。影像回归法可以用于处理不同时期影像的均值和方差存在差别的情况。

5.变化向量分析法

多光谱遥感影像数据可以用一个具有与影像光谱分量相同维数的向量空间来表达。影像中一个特定的像素可以用此向量空间中的一个点来表示，向量空间的坐标与相应光谱分量的亮度值有关。因此，与每个像素有关的那些数据值在多维空间中定义了一个向量。如果一个像素在时间t1到t2内发生了变化，向量描述的变化可以用t2时的向量与t1时的向量的差来定义，这个差向量就称为光谱变化向量。如果使用这个变化向量分析两个时间影像的变化，则称它为变化向量分析法。如果光谱变化向量的幅值超过了某个特定的阈值，就认为发生了变化。这个向量的方向包含了变化类型信息。

6.主分量分析法

主分量分析法(PCA)使用主要分量变换。在原始数据的协方差或相关矩阵中，我们可以发现:如果一个线性变换定义了一个新的直角坐标系，那么数据就可以表达成不相关形式。新坐标系的各个轴由矩阵的相应特征向量定义。每个像素可以用它的原始向量(如像素亮度值)和特征向量的向量乘积进行变换，然后可以得到新空间(如一个新像素向量)的坐标。每个特征向量可以看成一个定义的新波段，并且，每个像素的坐标可以看成它在那个“波段”中的亮度。每个新“波段”所表达的总场景变化量由相应特征向量的特征值给出。PCA已经应用于由两个或多个日期的波段所组成的影像数据序列中。当区域没有显著变化时，影像数据之间会有很高的相关性，而当区域发生了显著的变化时，它们的相关性就会很小。假设多时相影像数据序列中的变化的主要部分与恒定的类型相关联，那么有局部变化的区域会在由影像产生的更高的主分量中得到加强。协方差矩阵确定的主分量与那些使用相关矩阵确定的主分量有所不同。

7.归一化影像差值法

归一化影像差值法对原始影像差值法作了一点改变，在这一方法中，两幅影像在比较之前进行了归一化，产生了具有可以比较的均值和方差的影像，经过归一化后的影像再相减生成差值影像。有很多方法可以进行归一化，最常用的方法是使用均值和方差。影像的归一化可以通过式(14-9)进行:

归一化影像差值方法可以提高检测的性能，但是变换系数的选择非常重要。在归一化过程中，均值和方差需要在变换前迸行计算，也增加了程序运行的时间。

8.内积分析法

在内积分析方法中，像素灰度值被看作多光谱的向量，两个向量之间的区别通过两向量间夹角的余弦来表示，如果两个向量彼此一致，内积就等于1；如果两个不同时期的对应像素发生了改变，内积就会在－1和1之间变动。生成一幅单波段影像来记录内积，根据内积的不同值来体现影像变化。

设x(t1)，x(t2)为取自两幅不同时间影像对应像素的光谱向量，两向量的内积可以表示为

表面反射值的差异可以表示为

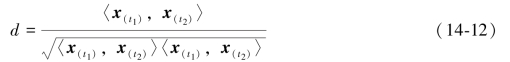
由于－1＜d＜1，内积可以用式(14-13)表示:

(www.xing528.com)

式中，a1、a0为两个常数，使得内积c能取得合适的非负间隔。

9.纹理特征差值法

灰度共生矩阵强调灰度的空间依赖性，其特点是体现了在一种纹理模式下的像素灰度的空间关系。此处用影像区域纹理特性值作为该区域中心像素的变化检测对象，我们选对比度作为纹理特征。

灰度共生矩阵的各元素值由式(14-14)确定:

式中，p(i，j，d，α)是灰度分别为i和j，距离为d且方向为α的像素点对的出现次数。

表达式为

式中，fij为纹理特征值，i，j为像素坐标值；t1、t2为两幅影像的获取时间，C为常量。

10.矩特征差值法

若将影像看作一个二维随机过程，标准化的中心矩具有平移、旋转、比例及线性变换不变性等优良性质，因而适于作描述影像的特性。在理论上，足够多的一组矩就可完全描述任何影像，与任何其他变换一样，低阶矩描述的主要是能量分布较大的概略信息，而高阶矩主要是描述影像中的细节信息。用影像区域不同的矩特性作为该区域中心像素的变化检测对象。

利用影像的二阶及三阶矩可以得出影像的七个不变矩，选取其中之一:

两影像相减，表达式为

11.自适应性典型相关法

典型变换是将两组随机变量之间的复杂相关关系简化，即把两组随机变量之间的相关性简化成少数几对典型变量之间的相关性，而这少数几对典型变量之间又是互不相关的。此方法将用来对提取的区域统计特性、区域纹理特性、区域矩特性进行筛选、重组，然后再变化检测。

12.相关法

影像相关是最基本的一种影像匹配方法。研究影像匹配的问题正是为了找出在所检测的两幅影像中“相同或相似的程度”，从而得到不同的区域即变化。显然，相关程度越大，变化越少；反之，变化则越大。相关系数测度是影像相关中最常用的方法之一。相关法是利用两个信号的相关函数，评价它们的相似性，对相似的程度进行量化，得出变化与非变化的结果，常用的相似度测度有:相关系数、相关积测度、协方差函数测度、差的绝对值和、差的平方和、互信息法。

13.小波变换系数差值法

将同一目标区前后时相的遥感影像进行小波分解，若目标未发生变化，两时相对应区域的小波系数接近，若目标发生了变化，对应区域的小波系数差别大。对两时相遥感影像各波段对应的小波系数求差，得到的小波系数在目标未发生变化的区域接近0，发生变化区域的小波系数绝对值大，能量高，因此当对其进行小波逆变换，得到的影像在目标发生变化处的图斑亮度值大，而未变化处的亮度值小，根据图斑亮度差异就可以区别出发生变化的目标。

表14-2对以上其中六种方法作了综合比较。针对如图14-8所示的武汉市某地2002年和2004年QuickBird影像，比值法变化检测结果如图14-9所示。图14-10和图14-11分别为建筑物和道路的变化检测结果示例。

表14-2　六种像素级变化检测方法比较

图14-8　变化检测数据源

图14-9　比值法变化检测结果

图14-10　建筑物变化区域放大后的检测示例

图14-11　道路变化区域放大后的检测示例

像素级变化检测方法简单且易于操作，但随着高分辨率遥感影像的普及，其缺陷越发凸显，影响变化检测精度的因素主要包括:①工作量大、效率不高；②检测结果对影像的辐射差异等外界影响较为敏感；③提取变化像素的阈值难以确定；④椒盐噪声明显。