城市遥感影像检索方法：低层视觉特征应用

本节介绍了常用的基于颜色特征、纹理特征以及形状特征的城市遥感影像检索方法，其中颜色特征包括颜色直方图、颜色矩、颜色熵和颜色相关图，纹理特征包括灰度共生矩阵、LBP纹理、Gabor变换和小波变换，形状特征包括几何不变矩和Zernike矩。

1.基于颜色特征的城市遥感影像检索方法

颜色特征是人类识别影像的主要感知特征，因此，其在影像检索的研究中获得了最为广泛的应用。基于颜色特征的城市遥感影像检索方法如图12-12所示。

图12-12　基于颜色特征的城市遥感影像检索流程

其中，可采用不同的颜色特征描述子，以下介绍几种常见的颜色特征描述子。

1)颜色直方图

在基于内容的影像检索中，应用最为广泛的颜色特征是颜色直方图(Swain et al.，1991)。颜色直方图特征通过不同色彩在整幅影像中的占比来描述影像内容。设I(i，j)为一幅影像，且(i，j)为影像中像素点的坐标，M和N分别为影像的宽和高，C为影像对应的颜色集合，c为其中任一量化颜色级，则影像的颜色直方图可表示为

其中，δ(·)表示狄拉克函数。颜色直方图的优点在于其提取方法简单、相似度计算量小、具备尺度和旋转不变性；缺点在于其只描述了影像颜色的统计特性，忽略了颜色在影像空间中的分布信息。

图12-13以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于颜色直方图的前10检索结果。

图12-13　基于颜色直方图特征的城市遥感影像检索

2)颜色矩

颜色矩(Stricker et al.，1995)思想源于影像中任何颜色分布均可以用其多阶矩表示。并且，由于颜色的分布信息主要集中在其低阶矩中，实践中通常利用颜色值的一阶原点矩(即均值)、二阶中心矩(即标准差)和三阶中心矩(即偏斜度)来描述影像的颜色特征。这三个低阶矩的计算公式依次为

式中，Ik(i，j)表示影像像素(i，j)在第k个颜色通道中的灰度值；M和N分别为影像的宽和高。通过式(12-24)可知，对于一幅具备三个颜色通道的彩色影像来说，其对应的颜色矩特征向量是一个9维的特征向量，可表达为

相比于颜色直方图，颜色矩的特征维数明显降低，同时在实际应用中，颜色矩通常结合其他特征一起使用，作为渐进式影像检索中的一个初检手段。

图12-14以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于颜色矩的前10检索结果。

3)颜色熵

图12-14　基于颜色矩特征的城市遥感影像检索

图12-15以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于颜色熵的前10检索结果。

图12-15　基于颜色熵特征的城市遥感影像检索

4)颜色相关图

颜色相关图(Huang，1998)除描述了不同颜色的像素在整幅影像中的占比之外，还可以表示不同颜色对之间的空间相关性。设I为一幅原始影像，Ic(i)为所有颜色为c(i)的像素的集合，则可将颜色相关图表示为

图12-16以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于颜色相关图的前10检索结果。

2.纹理特征

在遥感影像中，纹理主要是由地物特征如森林、草地、农田、城市建筑群等产生的。与地物光谱特征相比，遥感影像中地物的纹理特征相对更稳定，在高分辨率影像分析和识别中，特别是当遥感影像上目标的光谱信息比较接近时，纹理信息对于区分目标具有非常重要的意义。

图12-16　基于颜色相关图特征的城市遥感影像检索

基于纹理特征的城市遥感影像检索方法如图12-17所示。

图12-17　基于纹理特征的城市遥感影像检索方法

以下介绍几种常见的纹理特征描述方法。

1)灰度共生矩阵

由于纹理特征是相邻像素或区域间灰度空间分布规律的表征，因此具备相同位置关系的一对像素间的某种条件概率就可以用来描述纹理特征。灰度共生矩阵(Haralick et al.，1973)即按照这一思路，采用影像灰度值的空间关系描述像素点对之间的空间结构特征及其相关性，进而表示影像的纹理特征。

设I(x，y)为一幅原始灰度影像，R为影像中的任一区域，S为该区域中具备特定空间关系的像素对集合，则相应的灰度共生矩阵可表示为

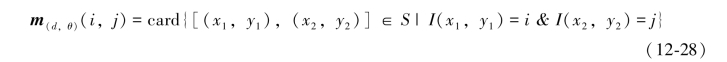
其中，x2＝x1＋dcosθ，y2＝y1＋dsinθ，card(S)表示满足集合S条件的像素对个数。在应用实践中，通常需要对式(12-28)进行归一化处理，表达式如下:

图12-18以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于灰度共生矩阵的前10检索结果。

图12-18　基于灰度共生矩阵特征的城市遥感影像检索

2)LBP纹理

局部二进制模式(Local Binary Pattern，LBP)通过计算每个像素与邻域内其他像素的灰度差异来描述影像纹理的局部结构(Ojala et al.，2002)，对于影像中任意一个3×3的窗口，比较窗口的中心像素与邻域像素的灰度值。若邻域像素灰度值大于或等于中心像素的灰度值，则该像素位置赋值为1，反之赋值为0。对于阈值处理后的窗口，将其与权值模板的对应位置元素相乘求和即可得到窗口中心像素的LBP值。

最初的LBP对纹理特征的描述是非常有限的，后续对其进一步改进，提出了可以检测“uniform”模式的、具有灰度和旋转不变性的描述子，如式(12-30)所示:

式(12-30)、式(12-31)中，R是圆形邻域的半径；P是圆上等间距的分布的像素数目；gc是圆形邻域的中心像素；gp(p＝0，1，…，P－1)是圆上的邻域像素。

Ojala等(2002)的实验表明，(P，R)取(8，1)时得到的LBP算子的uniform模式数量为59，可以有效地描述影像的大部分(87.2%)纹理特征并明显减少特征数量。

图12-19以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于LBP纹理特征的前10检索结果。(www.xing528.com)

图12-19　基于LBP纹理特征的城市遥感影像检索

3)Gabor变换

由于Gabor滤波法利用了Gabor滤波器具有时域和频域的联合最佳分辨率，并且较好地模拟了人类视觉系统的视觉感知特性的良好性质，在遥感影像纹理分析中颇受关注。首先，采用母Gabor小波作为2D Gabor函数，表达式如下:

公式(12-33)为式(12-32)的Fourier变换:

Gabor函数构建了一个完备但是非正交基，以2D Gabor函数作为母小波，通过对其进行如式(12-34)所示的膨胀和旋转变换，就可以得到自相似的一组滤波器，称为Gabor小波变换滤波器。

式中，a＞1，m，n为整数，θ＝nπ/K(n＝0，1，…，K－1)，a－m(m＝0，1，…，S－1)表示尺度因子。设Ul和Uh分别表示最低中心频率和最高中心频率，K和S分别表示多尺度分解中的方向个数和尺度级数。

对于给定影像I(x，y)，其Gabor小波变换可以定义为公式(12-36):

纹理特征可以采用公式(12-37)所示的向量来表示:

其中，μmn和σmn分别表示变换系数的均值和方差，计算公式如下:

相似性距离计算公式如式(12-39)所示，a(μmn)和a(σmn)用来实现归一化:

图12-20以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于Gabor特征的前10检索结果。

图12-20　基于Gabor特征的城市遥感影像检索

4)小波变换

采用小波变换来表达影像的纹理特征时，常用的处理方式是首先对原始影像进行多层小波分解，然后统计各个分解层上各方向子带系数的均值和标准差，以之表征子带系数的边缘分布并构建特征描述子。设原始灰度影像为I，对其进行M层小波分解后，可得3M个方向子带，设wmn(x，y)为第m层第n个方向子带上坐标为(x，y)的子带系数，且有m＝1，2，…，M，n＝1，2，3，则对应子带上均值μmn和标准差σmn的计算式为

在此基础上，即可构建如下特征向量用于纹理特征描述:

图12-21以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于小波变换特征的前10检索结果。

图12-21　基于小波变换特征的城市遥感影像检索

3.形状特征

相对于颜色特征和纹理特征而言，形状特征属于影像的中间层特征，通常与影像中的特定目标对象有关，包含一定的语义信息，对获取影像场景的语义描述尤为重要。

基于形状特征的城市遥感影像检索方法如图12-22所示。

以下介绍几种常见的形状特征描述方法。

1)几何不变矩

几何不变矩源于所提出的影像识别的不变矩理论，并且被广泛地用于影像模式识别及目标分类等领域。在不变矩理论中，Hu(1962)基于代数不变量的矩不变量，推导出了一组对于影像平移、旋转和尺度变化能够保持不变性的矩，以描述目标区域的形状特征。

对于任一影像f(x，y)来说，其p＋q阶矩的定义如下:

而其p＋q阶中心矩则定义为

图12-22　基于形状特征的城市遥感影像检索方法

上述7个不变矩组共同构成了Hu不变矩。该矩组中φ1～φ6具备平移、旋转和尺度不变性，并且φ7具备平移和尺度不变性。

图12-23以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于几何不变矩特征的前10检索结果。

图12-23　基于几何不变矩特征的城市遥感影像检索

2)Zernike矩

式中，n和m为非负整数，且需满足n－｜m｜为非负偶数。

Zernike矩的优点是具备良好的旋转不变性，其缺点在于不具备尺度不变形，因此在实际应用中，通常需预先进行归一化处理。

图12-24以遥感影像场景“机场”为例，给出了机场影像在UCM数据集上基于Zernike矩特征的前10检索结果。

图12-24　基于Zernike矩特征的城市遥感影像检索