城市遥感影像相似性度量:原理、方法和应用

图12-9　ResNet-18各网络层特征图

1.Minkowski距离

Minkowski距离是基于Lp范数定义的，其表达式为

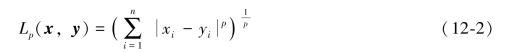
当p＝1时，L1(x，y)为曼哈顿距离，其表达式为

当p＝2时，L2(x，y)为欧氏距离，其表达式为

当p→∞时，L∞(x，y)为切比雪夫距离，其表达式为

2.直方图相交法

直方图相交法(Swain et al.，1991)具备简单、快速的特点，并能够较好地抑制背景的影响，其数学表达式为

式(12-6)还可以进一步做归一化处理(庄越挺，1998)，具体表达式如下:

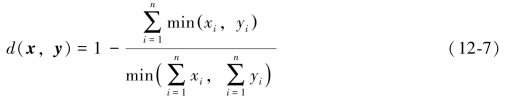
3.KL散度和Jeffrey散度(www.xing528.com)

KL散度(Kullback et al.，1951)用于计算两个概率分布之间的差异程度，其表达式为

4.χ2距离

χ2距离又称卡方距离(Rubner et al.，2013)，其数学表达式为

卡方距离的计算简单、快速，并且能够消除不同维度特征值之间的量纲差异，因此在影像检索中有着广泛的应用。

5.二次式距离

二次式距离(Hafner et al.，1995)作为一种颜色直方图的相似性度量准则，已被证实比欧氏距离和直方图相交法更加有效，其数学表达式为

式中，M＝(mij)，表示直方图中第i维和第j维颜色之间的相似度。由于引入了颜色相似性矩阵M，二次式距离能够更好地顾及相似但不同颜色间的相似性因素，使得颜色特征度量结果更好地符合人类视觉特性。

6.余弦距离

余弦距离表达的是两个向量间方向的差异度，其数学表达式为

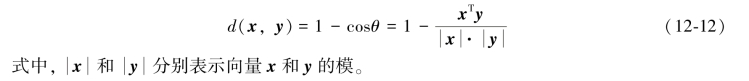
7.相关系数

相关系数通常用来描述两个向量之间的线性关系紧密程度，其数学表达式为

通过计算影像特征的距离来衡量影像的相似性是目前相似性度量的常用方法。但相比自然影像，城市遥感影像的场景更复杂，在影像特征确定的前提下需要设计更稳健的相似性度量方法来计算影像的相似度，从而改善遥感影像的检索结果。