城市遥感影像超分辨率重建方法

基于插值的超分辨率重建方法主要针对的是影像下采样导致分辨率下降的问题，而基于重构的方法旨在恢复降质过程中丢失的高频信息。基于重建的方法是对成像过程的数学模型进行求解，但是对影像降质模型的求解是一个病态的逆问题，符合条件的解有无数个。为了得到合理的解，需要相应地引入影像中实际存在的先验知识建立正则项，从而得到该病态逆问题的可行解，恢复降质过程中丢失的高频细节信息。基于重构的超分辨率重建可分为频域方法和空域方法两类，下文中对此两类进行简要介绍。

1.频域方法

由于图像的卷积、平移、旋转等运算都可以在频域转化为易于处理的算数运算形式，因此频域处理成为处理图像超分辨率重建问题的一个直接想法。在假设的低分辨率影像Yk的生成模型条件下，Tsai(1984)分别对观测到的低分辨率图像和目标高分辨率影像进行离散傅里叶变换(DFT)和连续傅里叶变换(CFT)，并根据傅里叶变换性质，在频域建立二者的线性关系:

其中，yk和x分别为低分辨率影像Yk和高分辨率影像X傅里叶变换并向量化后的结果。该方法首先通过计算得到生成模型的参数，确定线性变换关系Φk。这样，就把求解高分辨率影像X的问题转化为求解x，即为上式的逆问题。

由于频域计算本身的特性，这种基于傅里叶变换的频域方法在理论推导和计算上都有一定优势，支持并行化的运算处理，方便高效。但是，频域方法也有较明显的缺点:频域方法对噪声比较敏感，且难以在处理过程中添加先验信息。另外，由于频域与空域之间复杂的变换关系，传统的频域方法仅能处理输入低分辨率图像之间只存在全局整体运动的情况，而难以处理场景中存在物体相对运动的情况，局限性较大。随后，研究者又使用可以刻画图像局部性质的小波变换对图像中的局部不同情况进行处理，有效提高了重建影像的局部质量。

2.空域方法

基于重构的影像超分辨率空域重建方法可用以下优化问题表示:

式中，ρ·()和r·()分别为数据约束项和正则约束项函数，λ为正则项对应的系数。实际中，常用的数据项函数为

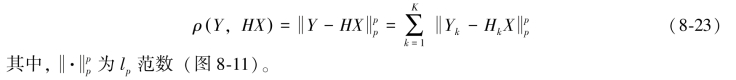
数据约束项函数保证了高分辨率影像降质之后的低分辨率影像与实际观测的低分辨率影像尽量相似。而正则项函数r·()包含先验知识的约束，根据不同的先验知识，可以设计出不同的正则项约束函数，常用的如光滑约束、保边缘约束等。

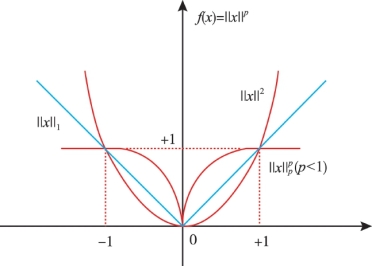
图8-11　lp范数中p取不同值时的函数示意图

下面介绍几种常用的基于重构的超分辨率重建方法，包括迭代反投影法、凸集投影法、最大后验概率等。

1)迭代反投影法(Iterative Back Projection，IBP)

迭代反投影算法的主要思想是通过迭代方式不断修正初始高分辨率影像。具体地，先根据观测到的低分辨率影像估测出一幅初始的高分辨率影像，对估测的高分辨率影像利用降质模型得到对应的低分辨率影像，然后将其与真实观测的低分辨率影像进行做差，再将差值反投影到高分辨率空间对初始估测的高分辨率影像进行更新。如此反复，直至误差小于指定阈值或达到迭代次数上限为止(图8-12)。

迭代反投影法思路简单，运算复杂度低，求解速度也相对较快，但是没有充分考虑降质模型的先验知识的约束，且反投影矩阵较难选取，最终得到的高分辨率影像不一定就是最合适的解。(www.xing528.com)

2)凸集投影法(Projection onto Convex Sets，POCS)

其中，Pi表示将高分辨率影像空间中任意一点投影到凸集Ci上的投影算子。

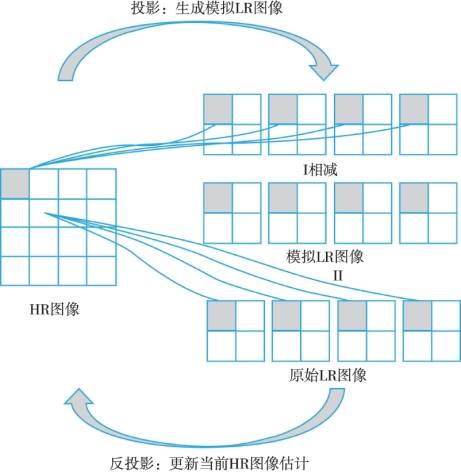
图8-12　迭代反投影方法示意图

凸集投影法包含先验信息的能力很强，可以加入各种先验信息的约束，如目标影像像素峰值约束等。凸集投影法是一种有效求解复杂优化问题可行解的方法，其优势在于思想简单直观，方法形式比较灵活，先验知识的加入比较方便。但是，凸集投影法的运算复杂度相对较高，收敛速度较慢，而且得到的是一系列可行解构成的集合，难以确定最优的解。

3)最大后验概率法(Maximum a Posteriori，MAP)

最大后验概率法是一种基于概率的超分辨率算法框架，将已知的低分辨率影像作为观测值，对目标高分辨率影像进行估计。根据贝叶斯公式，待求的高分辨率影像X可看作在当前低分辨率影像Y下，使得后验概率最大的影像，公式表述为

式中，P(X｜Y)表示在低分辨率影像Y已知的情况下，高分辨率影像X的后验概率；P(Y｜X)表示高分辨率影像X退化为低分辨率影像Y的条件概率，相当于数据误差项；P(X)表示高分辨率影像的先验概率，P(Y)为低分辨率影像的先验概率。对于已经观测到的低分辨率影像Y，P(Y)的值是固定不变的，也对式(8-25)没有影响。

因此，对式(8-25)进行进一步简化可得

用负log函数作用，进一步简化得到

其中，－logP(Y｜X)对应数据约束项，－log P(X)对应正则约束项。

MAP方法比较灵活，可以直接在高分辨率重建过程中对其进行先验约束，确保解的唯一性，算法收敛快且稳定性高。其中，正则项约束也可以根据不同问题进行灵活选取，也称为基于重构的方法的研究热点，较为常用的正则项包括二范数形式的Tikhonov正则项、一范数形式的全变分正则项以及双边全变分正则项等。

基于重建的影像超分辨率方法只是用了一些先验知识来正则化重建结果，这类方法的优点是简单、计算量低，但这种人工设计先验约束信息难以适用并处理具有复杂结构的影像。