插值方法重建城市遥感影像

基于插值的算法利用已知邻近像素的灰度值产生待插值像素的灰度值，是最为直观和简单的超分辨率重建方法，主要包括:最近邻插值、双线性插值、双三次插值和改进插值方法。

1.最近邻插值

而计算得到的理论位置数值可能存在小数，此时该点在低分辨率影像Il上无实际意义，此时应对其进行四舍五入，将影像Il中距离该理论点最近的一个点的值赋给它，得到最近邻插值的结果。最近邻插值法计算量较小，但可能会造成产生的图像灰度上的不连续，在变化地方可能出现明显锯齿状(图8-6)。

2.双线性插值

双线性插值又称一阶插值，它利用了周边与目标点相邻的四个点，分别在两个方向上作线性内插，权重通过目标点与相邻点之间的距离来确定，最终运算得到目标插值点的灰度值。在数学上，双线性插值是有两个变量的插值函数的线形插值扩展，其核心思想是在两个方向分别进行一次线性插值。

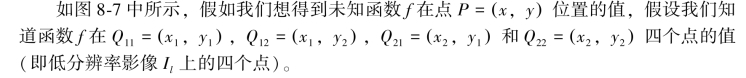
首先，在X方向上进行线性插值，得到

图8-6　最近邻插值结果示意图(插值倍数为8倍)

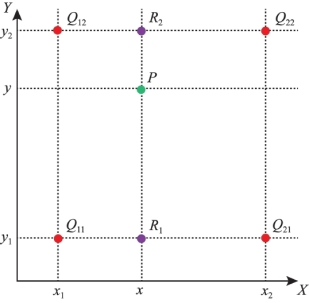
图8-7　双线性插值示意图

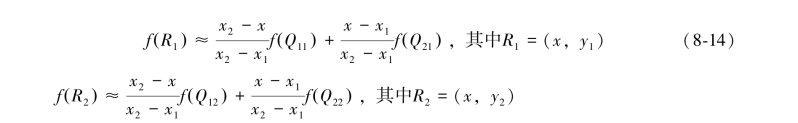
然后再在Y方向上进行线性插值，得到

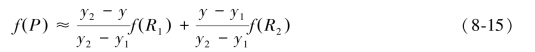
这样就得到函数f在P点的结果f(x，y)为

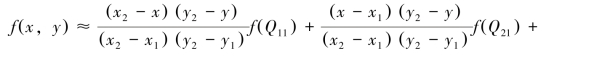
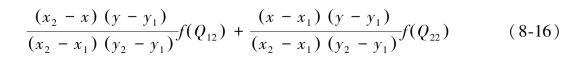(www.xing528.com)

如果选择合适的坐标系使得函数f的四个已知点坐标分别为(0，0)、(0，1)、(1，0)和(1，1)，那么双线性插值的公式可以简化为

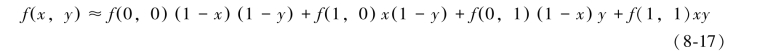
或者用矩阵运算表示为

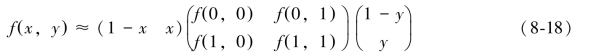
双线性插值的结果与插值顺序无关。先从Y方向进行插值，再从X方向进行插值，所得到结果都是一样的。双线性内插法的计算比最近邻点法复杂，计算量较大，但没有灰度不连续的缺点，插值效果较最近邻插值好。但是双线性插值具有低通滤波性质，使高频分量受损，重建图像轮廓较模糊(图8-8)。

图8-8　双线性插值结果示意图(插值倍数为8倍)

3.双三次插值

双三次插值(Bicubic Interpolation)在计算时利用了周围16个像素点的信息，利用三次多项式作为插值函数，使用的Bicubic基函数(图8-9)如下:

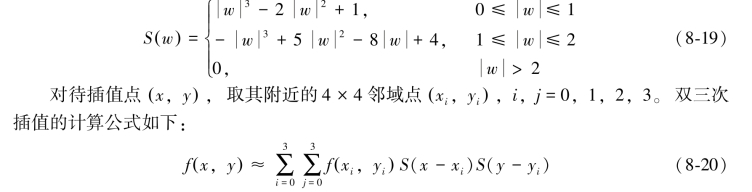
图8-9　Bicubic基函数形状示意图

相较于最近邻插值和双线性插值，双三次插值能够较好地保持重建影像的边缘(图8-10)。

图8-10　双三次插值结果示意图(插值倍数为8倍)

4.改进插值方法

为改善上述传统插值方法(最近邻插值、双线性插值和双三次插值)结果中的边缘模糊、振铃等效应问题，研究人员又相继提出了一系列改进的插值算法。例如，非均匀插值算法的适用对象是一组具有空间转移的低分辨率影像，采用广义多通道采样定理对这些影像进行插值。这种方法计算量小、具有实时性，然而忽略了插值误差，难以保证重构的最优性，有一定的局限性。Bose等(2006)基于多项式近似估计，针对不同像素点自适应调整参数，采用最小化运动方差的方式对邻域像素进行估计，进而推测超分辨率重建后各个像素对应的值，这种插值方法着力于更好地对影像边缘进行匹配。除此之外，还有如结合神经网络的插值算法、基于最小二乘的插值算法以及空间自适应插值算法等。相较于传统插值算法，这些改进的插值算法较好地改善了插值影像的边缘效应问题，取得了更好的插值结果。