PCB图像定位与配准技术

由于PCB有四角的定位标记（以两相互垂直的定位细线交点作为标记位置），并且Gerber文件同样有四个标记位置，因此可将定位标记作为特征点，采用基于特征点法的图像配准，匹配标准图像坐标与扫描图像坐标的双线性变换系数，完成图像配准。

1.基于Hough检测定位孔的PCB定位

为了定位的方便，一般的PCB上都会有各种形状的铜制Mark，如图7.6所示。Mark一般分布于PCB的四个角上，至少需要其中的三个来完成图像的定位配准。

图7.6　PCB定位Mark

露铜的同心圆是最常见的Mark形式，要将其从图像中提取出来，常见的检测方法有模板匹配、曲线拟合以及Hough变换等。前两种方法对图像的质量要求过高，在噪声较大或者导致圆弧的特征受损的情况下检测结果并不理想，Hough变化抗噪性强，变换精度高，但因为计算量过大、内存占用过多，所以其检测速度并不理想。采用限制累加范围与粗细累加相结合的方法能实现对圆形Mark的快速检测。

Hough变换是一种在参数空间内描述曲线的方法，首先将图像空间映射到参数空间，并以某种使大多数边界点都满足的参数形式来描述该曲线。通过设置边界点累加器，求出对应的累加峰值点，算出描述曲线所需的参数。

其中，（a，b）为圆心坐标，r为半径。确定了a，b，r三个参数就能准确地描述一个圆形。a，b，r在参数空间表征为一个圆锥，其顶点由（a，b）决定，受半径r的约束。圆形的半径是固定的，所以圆在参数空间中就对应为r相同而a，b不同的圆锥的集合。在参数空间需要使用一个三维的参数累加器来进行圆形的检测，因为图像的DPI是确定的，结合解析Gerber文件得到的r，就能算出r的像素值，从而将累加器降低成二维。通过阈值分割算法可将Mark从背景中分离出来，该过程为：先将图像转换为灰度图像，再对Mark附近的区域进行灰度直方统计，在本系统的光源条件下，Mark所成像和背景差异很大，因此灰度直方图存在双峰，选其谷值为分割的阈值，灰度图像中灰度级大于阈值的部分则为Mark。然后根据式7-2、7-3将（a，b）的大致坐标计算出来：

确定了r，计算出了（a，b）的大致范围，就能对累加范围进行限制，大大减少了计算量，实现对圆形Mark的快速准确定位。从图7.7可以看出，配准结果已经达到了亚像素级，其中黑色图像为Gerber图像信息。

图7.7　配准结果

2.基于控制点的图像配准

控制点的方法是基于特征配准的一种。该类方法主要共同点首先要对待配准图像进行特征提取，再利用提取到的特征建立匹配映射变换，再将其应用于畸变图像从而得到配准结果。这类方法的优点在于它提取了图像的显著特征，大大压缩了图像的信息量，计算量的剧减使得在有效配准的前提下同时兼顾了实时性。

IPT提供了一个交互式选择控制点的函数cpselect，可以利用该函数采取手动的方法在两幅图像的对应部分选取配准控制点，并自动进行亚像素分析。待配准图像（a）与标准图像（b）如图7.8所示

图7.8　待配准图像与标准图像

下面的代码演示交互式选择控制点的过程：

clear all；

clc；

I1=imread（'unregistered.jpg'）；

I2=imread（'standard.jpg'）；

unregistered=I2；

rect=Il；

cpselect（unregistered，rect）；

图7.9　控制点选择

在程序中，cpselect提供了交互式选择控制点的界面，如图7.9所示，左上角为标准图像，右上角为待配准图像。

fixedPoints=round（fixedPoints）；

movingPoints=round（movingPoints）；

input_points_corr=pcorr（movingPoints，fixedPoints，unregistered，rect）；

tform=cp2tform（input_points_corr，movingPoints，'linear conformal'）；

registered=imtransform（unregistered，tform，'XData'，［1 300］，'YData'，［1 300］）；(www.xing528.com)

这段程序根据用户在交互界面选择的控制点对图像进行重采样并配准，如图7.10，蓝色点为控制点所在位置。最终配准图像如图7.11所示

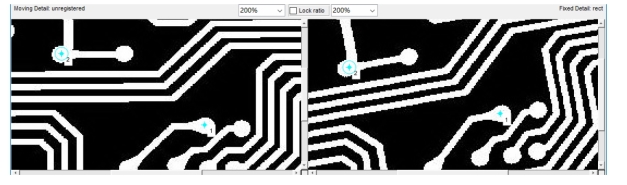
图7.10　控制点选择

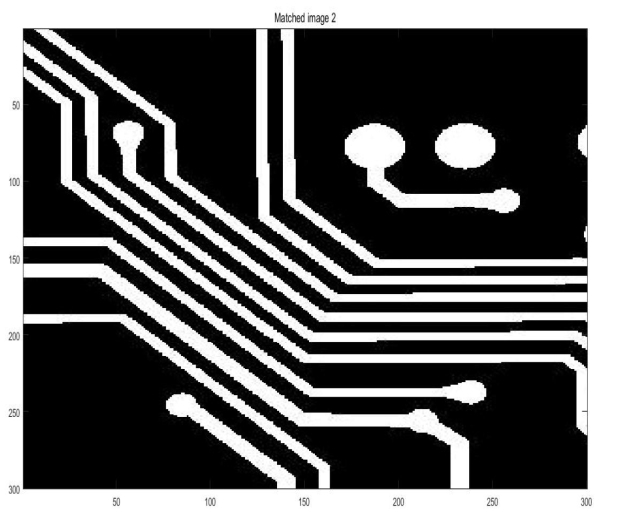
图7.11　配准图像

3.基于Harris角点特征的图像配准及其算法实现

基于特征的图像配准，即特征结构为图像中的特征点。特征点可以是图像中的线条交叉点、边界封闭区域的，或者曲面的高点等等.一旦在两幅图像中选定了两个特征点集后，有若干方法可以用来匹配两个特征点集，这些方法包括对两个点集的最小间距树进行分类、松弛和匹配，对两个点集的凸部边缘进行匹配等。

基于特征的配准方法，需要进行相关计算的像素点数目有了明显的减少，并具有更强的适应能力，这种算法的关键是寻找易于识别和区分的特征，基于特征集之间的相似性度量来找到模板在图像中的匹配位置。

角点是图像的重要局部特征，其直观定义是指在至少两个方向上图像灰度变化均较大的点，在实际图像中，轮廓的拐角、线段的末端等都是角点。角点特征因具有信息量丰富，便于测量和表示，能够适应环境光照变化，尤其适用于处理遮挡和几何变形问题等优点而成为许多特征匹配算法的首选。

Harris算子是根据在交点处图像的灰度梯度是不连续的，而且在角点临近的区域，梯度有两个或者两个以上的不同值得出的。这种算子受信号处理中自相关函数的启发，给出与自相关函数相联系的矩阵M，M阵的特征值是自相关函数的一阶曲率，如果两个曲率值都很高，则认为该点便是角点。

Harris算子的公式只涉及图像的一阶导数，对灰度图像上的每个像素点，计算其在横向和纵向的一阶导数，以及两者的乘积，这样就可以得到三幅新的图像，三幅图像中的每个像素对应的属性值分别代表gx、gy以及gxgy。然后进行高斯滤波，计算每幅图像上对应的每个点的兴趣值如式子：

式中gx为x方向的梯度，gy为y方向的梯度，G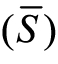（为高斯模板，k取0.04为权值系数，det为矩阵的行列式，tr为矩阵的迹。

4.角点匹配及其算法实现

所谓角点匹配是指找出两图像中的唯一对应角点，本节主要介绍一种基于奇异值分解的角点匹配算法。

有两幅图像门I和J，分别包含m个特征点和n个特征点，则基于奇异值分界的特征匹配算法包括以下三部分内容：

首先，分别取特征点Ii和Jj的W*W的邻域4和B，得到这两个区域的互相关系数：

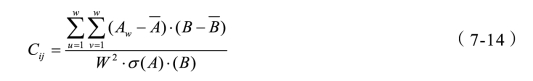
其中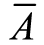，和分别为区域A和B的均值，σ（A）和σ（B）分别为区域A和B的标准差，可以看出互相关系数Cij取值范围为［-1，1］，当Cij=-1时表示两区域完全不相同；当Cij=1时，表示两区域完全相同。

然后，构造相似矩阵G，其中Cij是两个特征点Ii和Jj高斯加权的距离表示，即

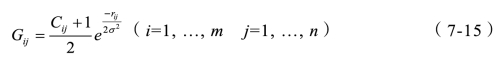
其中，rij=‖Ii-Jj‖表示两个特征点之间的欧式距离。Gij为正值，且变化范围为［0，1］。参数σ是用来控制两个特征点之间的相互作用，可以看出，当σ比较小时，Gij值比较大。

最后，对相似矩阵G进行奇异值分解：

其中，T∈Mm，U∈Mn并且都为正交矩阵；D为对角阵，D∈Mm，n，D中对角线元素按降幂排列，将D中对角线元素值不为0的元素置1，构造矩阵E，进而可以得到矩阵P：

矩阵P和G具有相同的形状，而且它可以很好地突出相匹配的特征点，抑制非对应的特征点。如果Pij为所在行的最大值，也为所在列的最大值，则特征点Ii和Jj为一一对应点，否则Ii和Jj不完全匹配。

特征点匹配算法需要满则三个准则：

①相似性准则：两个特征点所在的区域应相似；

②相近准则：两幅图中的两个特征点不应相距很远，对满足相似性准则的几个特征点，选择最近的两个点；

③唯一性准则：特征点匹配应该是一一对应的。

根据以上特征点匹配过程，G为相似性矩阵所以该算法满足相近准则，同时矩阵T和U为正交矩阵，因此该算法满足唯一性准则。而且，在相似性系数中考虑了距离的影响，该算法也满足了相似性准则，因此该算法的抗噪声性较强，对于有噪声的图像，使用该算法进行处理，提高了匹配的鲁棒性［17］。