自组织映射网络SOM也被称作Kohonen映射,是基于“竞争学习”的一种网络,与一般竞争式学习神经网络不同的是,自组织映射在竞争之后,不只获胜神经元有机会学习,它周围的神经元也能够学习。与传统模式聚类方法相比,它所形成的聚类中心能映射到一个曲面或者平面上而保持聚类结构不变,对于未知聚类中心的判别问题可以用自组织映射来实现。
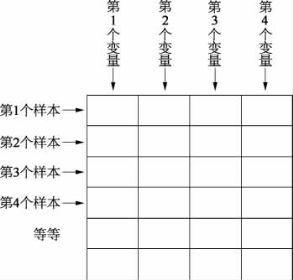
图22.9 输入样本描述
1)算法对数据的要求
该算法处理的数据类型称为电子数据表或者列表数据,表格的每一行都是一个数据样本。如图22.9所示,每一行的分项是数据集的变量或者分量,变量可以是一个目标的特性或者是在具体时间测量的物理量的集合。对网络输入样本的基本要求是,每个样本具有相间的变量集。
2)算法流程
实现SOM算法主要包括以下几个步骤:
(1)设定变量。
X=[x1,x2,…,xm]为输入样本,每个样本有m维向量。ω(k)=[ω1(k),ω12(k),…,ωm(k)]为第i个输入节点与输出神经元之间的权值向量。
(2)初始化。权也使用较小的随机值进行初始化,并对输入向量和权值做归一化处理:

变量的标定是非常重要的,因为SOM算法使用欧几里得度量来测量矢量之间的距离。如果一个变量值在[0,…,1 000]范围内,另一个变量的值是在[0,…,1]范围内,因为前者对距离度量起的作用较大,所以它将几乎完全控制图形组织。通常希望各个变量同等重要。实现这一想法的默认方式是线性的度量所有变量,所以每个变量的方差等于1。(https://www.xing528.com)
(3)将随机抽取的样本输入网络。样本与权值向量做内积,内积值最大的输出神经元赢得竞争。由于样本向量与权值向量均已归一化,因此内积最大相当于欧式距离最小:
![]()
求得距离最小的那个神经元,即为获胜神经元。
![]()
(4)更新权值。对获胜神经元拓扑邻域内的神经元,采用Kohonen规则进行更新:
![]()
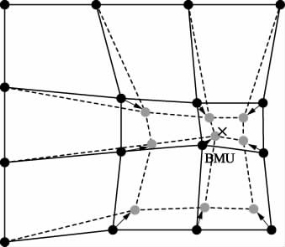
图22.10 更新的神经元示意图
找到获胜神经元BUM后,SOM的权矢量被更新,已知在输入空间,获胜神经元移动靠近输入矢量,其邻域也被同样处理。图22.10给出了这个适应过程获胜神经元和它的拓扑邻域朝向样本矢量的过程,实线和虚线分别对应更新前后的情况。
(5)更新学习速率η及拓扑邻域,并对学习后的权值进行重新归一化。学习率和邻域大小的调整分为排序阶段、调整阶段两步。
(6)判断是否收敛。判断迭代次数是否达到预设的最大值,若没有达到迭代次数,则转到第三步,否则结束算法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




