SWIM用于测量2D波谱，即波高或波斜率的密度谱，作为2D波数矢量k［此处以极坐标（k，φ）表示］的函数。我们首先回顾一下波高谱F（k，φ）被定义为表面位移的瞬时空间自相关的傅里叶变换。在极坐标系中，波斜率谱E（k，φ）与波高谱F（k，φ）的关系如下：
E（k，φ）=k2F（k，φ） （18.10）
波的总能量通常由有效波高Hs表示：
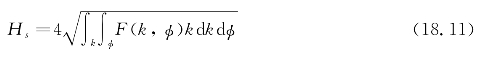
在20世纪90年代，杰克逊提出了一种替代SAR系统的概念，用于测量机载和星载配置的定向海洋波谱。该波谱是在各种机载系统上实施和验证的，例如由Jackson等人开发的Ku波段雷达海浪波谱仪（Radar Ocean Waves Spectrometer，ROWS），C波段系统RESSAC，C波段极化系统STORM，以及最近的Ku波段KuROS雷达。尽管2000年建立了星载仪器的初步设计，但SWIM将是第一个基于这一原理的星载仪器。
仪器原理使用的事实是，在低入射角（大约8°～10°），标准化雷达截面对与长波倾斜相关的局部斜率敏感，但对风的小尺度粗糙几乎不敏感，以及由于短波和长波相互作用引起的流体动力学调制。
对于天线的每个方位角方向φ，平均海面上的位置可以由其水平局部坐标x和y限定，其中x是沿天线指向方向的水平距离，y是沿方位角方向。基本反向散射截面σ由σ=σ0A给出，其中A是雷达距离门内包含的区域。大海浪的存在产生σ的倾斜调制，由下式给出：
式中，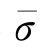
（x，y）是如果不存在大尺度波，则会出现的平均地面雷达横截面。该横截面仅取决于在该入射范围内具有有限冲击的小尺度粗糙度。
标准化雷达横截面沿波传播方向的分数变化如下：
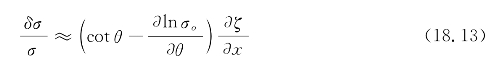
利用实孔径雷达，将雷达所看到的横截面的分数调制m（r，φ）横向平均通过波束，然后从调制Pm（k，φ）的密度谱中获得海浪极对称高度谱F（k，φ）：
其中〈α〉是在以下系数的光束中心估计的值：
其中，Ly是波束的3 dB方位角宽度。
为了获得式（18.14），假设Ly尺寸远大于待监测的波长，这显然可以满足卫星配置（Ly大约为18 km）。函数〈α〉k2称为倾斜调制传递函数。
假设由于散斑和热噪声引起的信号波动可以忽略不计，密度谱Pm（k，φ）从测量中获得(www.xing528.com)
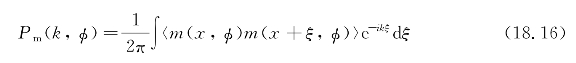
其中m（x，φ）是针对每个雷达方位方向φ，信号调制m（r，φ）投影在表面上，并且尖括号表示整体平均值。
实际上，信号受散斑和热噪声的影响，这些噪声在傅立叶域中是相加的。为了从信号波动中正确地检索波谱，必须将这些噪声的影响降到最低。对于热噪声，通过指定适当的信噪比来实现的。对于散斑，首先通过对发射脉冲使用大带宽来实现。然而，通过平均技术减少散斑仍然是有限的，因为从等式（18.16）中检索波谱需要高范围和时间分辨率。因此，必须在光谱域中减去散斑，其中信号波动谱可以表示为：
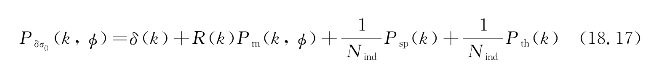
式中 Pδσ0——信号波动的密度谱；
Psp和Pth——分别是由散斑谱和热噪声引起的信号波动的密度谱；
δ（k）——狄拉克函数；
R（k）——脉冲响应的密度谱；
Nind——信号估计中使用的独立样本的数量（时间和距离的积分）。
假设发射脉冲具有高斯形状，Jackson等表明散斑的光谱可表示为其中，Kp与投射在表面上的雷达dr的固有分辨率有关：
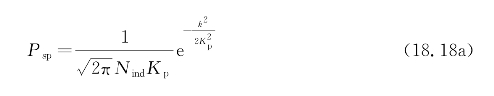
从信号调制估计无偏波能量的挑战之一是散斑噪声的影响，散斑噪声的能量与雷达信号中包含的独立样本的数量成反比。这些独立样本数量取决于雷达特性（多普勒带宽）和散射的相干时间。尽管Nind中的不确定性不会影响能量在波数和方向上的传播，但它可能会影响密度谱能量的估算。当从SAR观测或从实际孔径SWIM型观测估算波谱时，会出现这个问题。然而，在SWIM情况下，出现了另外一个问题，因为多普勒带宽随着天线的方位角位置而变化，并且当天线指向飞行轨道时倾向于零。此外，海上散射的相干时间尚不清楚，可能取决于地球物理条件（风、波浪）。因此，特别注意SWIM数据处理中的散斑噪声估计和校正。
图18.12 光束中心位置图
根据6个光束（0°黑色，2°红色，4°绿色，6°蓝色，8°青色和10°粉红色）的沿轨道距离（单位：m）和横轴距离（横轴：m）的函数显示每个循环的光束中心位置。水平条界定对应于2级近实时产品的不同框。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
