在扭转期间,当把姿态计算应用到两体引力模型中,研究误差就可以获得一个有用的结果。计算两组位置向量就可以建立一个两步的仿真,第一组用于两体模型,第二组用于高精度轨道计算(HPOP)模型。在第一步里,两体位置向量用来寻找磁场位置。当给定飞行器的初始前坠姿态、速率,在飞行器处于稳定时,最优扭矩曲线就能被确定。在第二步里,通过已经得到的扭矩和HPOP位置向量来重新计算卫星真实位置的磁场。由于两体模型存在位置误差,磁场随着空间的变化而变化,所以应用的扭矩不再是最优的。仿真的目的是研究误差对ADCS算法的精度和稳定时间的影响。
在这一章里,位置向量的幅度误差初期估计约为7 km。这个结果在图16.11再次出现,从图中还可以看到通过用双位置计算模型获得由磁场引起的误差,相对较大的位置误差对磁场几乎没有影响。举个例子,第一个最大位置误差大约在仿真开始后的半小时出现。同时在两个位置上计算的磁场基本是相同,都接近最高点。当位置误差接近零的时候,在横轴为1.5的点上可以从反方向来看这个仿真图,但是所计算的磁场误差有所增加。
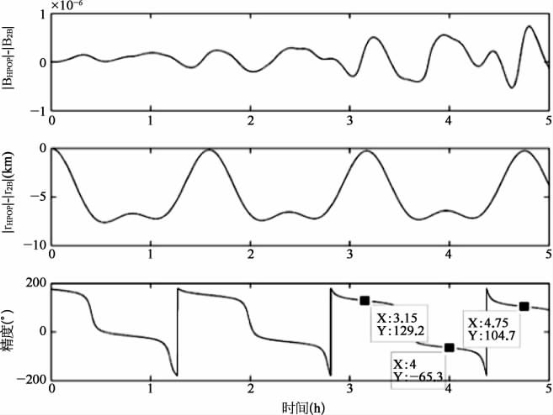
图16.11 计算的磁场误差来源
为了理解这些非直观的结果,把相应的飞行器经度也描绘出来了,并且可以在同一个图上看到。图中表明经度的是三个点,这三个点与磁场误差图中的三个较大峰值相对应。仿真开始后,这些峰值大约出现在横轴为3.15、4.00、4.75的时间点上,并且分别与精度大约为125°、-62°、103°相匹配。在看图16.3中的磁场等势线时,这些经度的重要性就变得特别明显。在经度大约为125°的地方有两个大的异常磁场。一个位于亚澳区域,另一个位于西伯利亚北部区域。ION的飞行轨迹经过这两个异常磁场时,它的倾斜角为98°。磁场中第一个约为0.5×10-7的幅度误差与亚澳异常磁场和赤道磁场之间的陡峭梯度有关。一旦卫星进入磁场强度接近常数的赤道区域,与位置误差有关的磁场误差就会减小到0。然而,在这之后,卫星进入西伯利亚北部异常区域时,即使很小的位置误差也会导致较大的磁场幅度误差。相似的结果可以在经度为300和100的地方看到,分别是图16.3中的南大西洋和北美洲异常区域。
将非最优化的扭矩应用到了航天器上会造成上述计算的磁场与实际磁场存在误差。最初这个影响很小,但是随着航天器姿态逐渐偏离预定的状态,应用扭矩变得越来越不理想。通过绘制应用扭矩的预期和实际响应图(已经在图16.12中绘制),可以建立一个近似时间,在这个时间内扭矩是精确的。结果随着轨道位置和扭转时间而变化,无论卫星是处于异常磁场中还是处于强化的应用扭矩下,下面的结果可以表示一个执行ION任务的过程中遇到的很典型的误差。在图16.12中可以看到,姿态开始出现偏离大约在仿真开始后的1.5 h,2 h达到了一个不可接受的偏离程度。这个结果使我们对双体计算模型的能力有信心,其可以被成功地使用,因为预期的能量预算允许的最大值为一个小时的连续扭转。在所有的方案中,最初给定卫星最大的前坠速率为5°/s,并且在飞过异常磁场的过程中必须使用磁力扭矩。另外,在图16.13中可以看出精准扭矩持续时间的局限性,在最低点方向比较了预期与实际的偏移。结果证实,在扭转两个小时后,卫星的z轴开始偏离预期的姿态。(https://www.xing528.com)
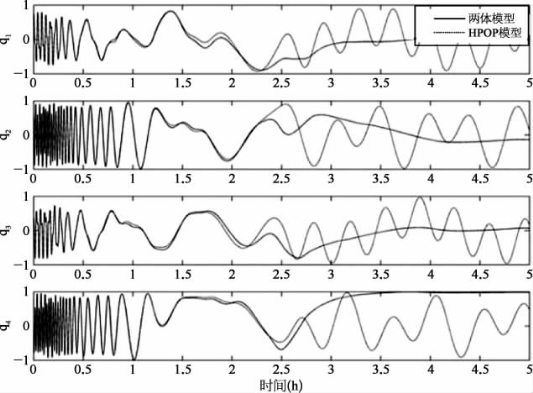
图16.12 两体模型和HPOP模型四元数的演变
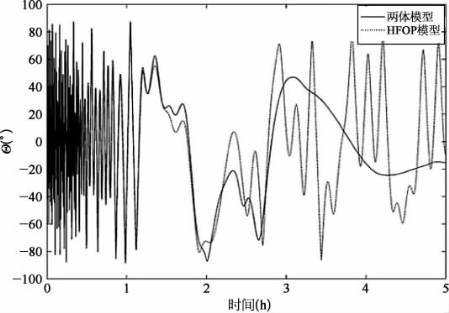
图16.13 两体模型和HPOP模型最低点偏移角的演变
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




