海洋智能无人系统姿态估计

姿态的确定是一个独特的问题，其中只测量出一个向量是不能计算出姿态的，并且整个系统处于不确定状态。同时，测量两个向量会提供过多的信息，迫使问题超定。其结果就是大多数的姿态确定算法就是姿态估计算法，ION也不例外。

ION姿态估计算法使用三个传感器信息的组合，在沿着轨道的离散点上，根据其轨道位置计算出其姿态。设计的实现过程是使用两组向量确定姿态。第一组向量包括在卫星体系里的磁场和太阳方向，这些信息是从卫星体框架下的磁力计、太阳传感器和电池板获得的。第二组是在ECI体系中的磁场向量和太阳方向向量，这两个向量是基于卫星的轨道位置计算出来的。该方法的细节将在下面部分介绍。

1）板载传感器的太阳方向向量

图16.8展示了当ION处于轨道上有阳光的地方时，太阳能电池板和顶部的太阳能传感器是如何照射的。根据太阳能板顶部电池的电压读数，角度α3可以很快地计算出来，将其代入式（16.11）。

所产生的电流和入射角之间的关系可以写成：

I=Imaxsinα　（16.12）

其中在图16.9中确定α，Imax为当太阳直射太阳板时所产生的感应电流。

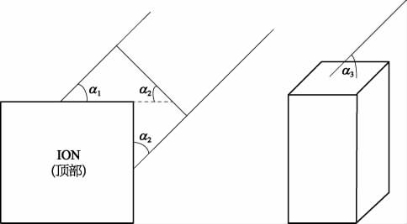
图16.8　太阳入射角图

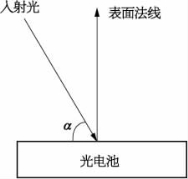
图16.9　光电图

用式（16.12）可以得到卫星两边的电池所产生的电流之间的关系，建立一个比例系数，结果如下：

另一个维数α2可以从以下的关系式中得到：

sinα2=sinα1（16.14）

最后，如式（16.15）所示，使用前面的方程，图16.8中的几何关系可用三个入射角来表示。在这种形式下，假定入射光束相交于x，y的正轴、z的负轴上，那么方程描述了在卫星的固定框架中的太阳矢量。

2）来自JulianDate的太阳方向向量

通过板载传感器获得太阳的位置后，下一个步骤是计算基于JulianDate的太阳矢量。JulianDate是表示任何天文现象的全球时间所普遍采用的手段将其定义为自4 713 B.C格林尼治中午（12∶00）以来的天数。

但是，因为JulianDate不是给卫星任务安排时间表和显示姿态经历最直观的方式，在整个ADCS软件中都是使用这种通用的格式：［年；月；日；小时；分钟；秒］。由于这两种时间格式的使用，式（16.16）给出了两者之间的转换关系：

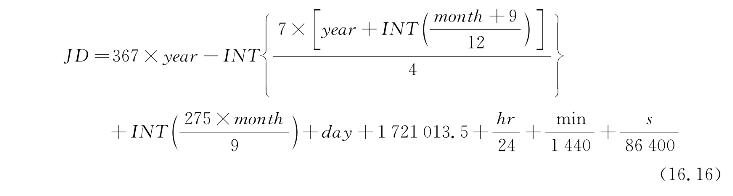
在制定ECI框架中的太阳矢量时必须记住，黄道平面与赤道平面的倾斜角度为ε，被称为黄赤交角，这可以在图16.10看到。图中还显示的是太阳矢量的经度，这是从春分点的方向沿着黄道面测得的。

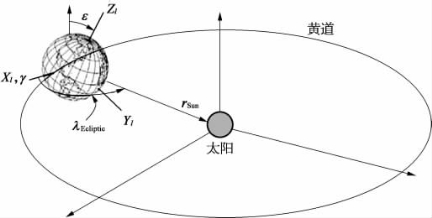
图16.10　相对于ECI框架的黄道平面

作为一个中间步骤，定义一个中间变量是非常有用的，这个变量称为太阳的平均经度，如下所示：

其中TUT1是用通用时间来表示的期望时刻，可以根据JulianDate，使用下面的方程来计算：

下标1指的是通用时间的形式，通用时间纠正了极地运动并和天文站台位置无关。想更进一步地了解UT的差异，请参阅文献。

接下来，有必要用下式（16.19）来计算太阳的平均近点角MSun：

(www.xing528.com)

其中TTDB是重心动态时间，可近似估计为TUT1。根据前面的等式，可以写出太阳的黄道精度λEcliptic如式（16.20）所示：

与等式（16.19）的假设相同，即TTDB≈TUT1，赤道倾角可以得到精确的估计，如式（16.21）所示：

最终可以用下面的形式在ECI框架写出太阳的矢量：

3）确定性姿态

姿态确定的本质就是寻找卫星固定体的参考框架和一些惯性系（如ECI框架）之间的旋转矩阵的问题。可以看出，只需要三个量就可以完全确定一个方向的余弦矩阵。同时，由于单位向量的约束性，每个单位矢量仅能提供两个信息。因此，有必要使用两个向量，这将提供四个已知数，使问题超定。

在理想情况下有四个向量，可以写出如（16.23）和（16.24）的式子，同时两个矩阵也是相等的。但是因为该系统是超定的，通常是不可能找到这样的AB／I矩阵。

为了解决这个问题，使用一个三元算法丢弃一个信息。但是请注意，该方法不是简单的丢弃测量信息中的一个，还需注意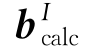是在ECI框架中计算出的磁场矢量，是由向量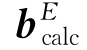转变成惯性系获得的。

三合算法使用矢量信息压缩的方法，构造了两组正交单位矢量。两个三合算法同样是参考框架和惯性坐标系的组成部分，其中参考框架在卫星主体中用t表示。假设主体／惯性向量组中的一个向量组是正确的，参考框架就可以被创建。在下面的推导中，假设太阳矢量是正确的，由以下定义的向量开始这个推导过程。

下一步包括构造一个二阶基向量作为一个单位向量，该单位向量垂直于另外两个观测向量。

计算出来的第三个基向量用于计算正交三元组，公式如下：

通过将t向量变成3×3矩阵的列向量就可以构建出两个旋转矩阵如下：

进一步观察，前述的矩阵分别是AB／t和AI／t，因此参考框架I和B之间的旋转矩阵可以通过如下方式计算：

式（16.32）定义了在ECI框架下，我们所期望的卫星姿态。

4）转速估计

前面部分描述了如何及时地计算卫星的瞬时姿态方法。但是，在实际的操作当中很有必要知道卫星在任何时刻的姿态，这样就不用传感器重新采样了。幸运的是，如果我们知道卫星的转速就可以完成上述要求。反过来说，就是通过拉格朗日插值公式，简单地计算出三个独立姿态测量值中的最小值即可。也可以将三个姿态值代入到拉格朗日插值公式中，计算出最小的一个即可。在这里只是给出了最终的结果。

回顾三元组算法，根据式（16.32）算出一个旋转矩阵AB／I。用下面的式子可以很方便地将这个姿态矩阵转换成欧拉角φ，θ和ψ。

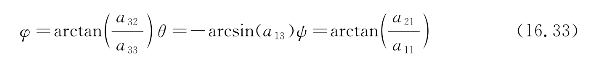
然后在这三个独立的采样点上，每个点的这三个欧拉角都要重复计算，这三个采样点与测量的时间t1，t2和t3相对应。因此角速度可以通过以下式子计算出来：

在最后的时刻t3处，注意到以上方程是专门用于计算角速度的。这个问题在下一章会详细说明，控制算法在离散点的姿态和角速度处读入，并且计算那个时刻的最佳驱动扭矩。虽然很可能获得三个时刻中任何一个时刻对应的卫星姿态和转速，但是根据过时信息（比如时间t1和t2）计算的最优扭矩是很不合适的。