下一步是计算卫星位置的磁场向量，这一步主要是用于ION的姿态估计。图16.3显示了地球磁场等高线的分布，该分布投影在墨客托地图上。从图中可以看出磁场的分布是不均匀的，但是从图中无法看出磁场是随时间变化的，因此在计算时相当困难。
1）国际参考地磁场
国际地磁学与高空物理学协会（International Association of Geomagnetism and Aeronomy，IAGA）对地球主磁场展开了描述，称其第十代磁场为国际参考地磁场（international geomagnetic reference field，IGRF）。地球主磁场和其年度变化率是IGRF的数学模型。主磁场系数是时间的函数，并假设IGRF在五年内的变化是线性的。因此可以精确地计算出未来几年的IGRF磁场，其次还可以推断过去五年时间内的磁场系数。
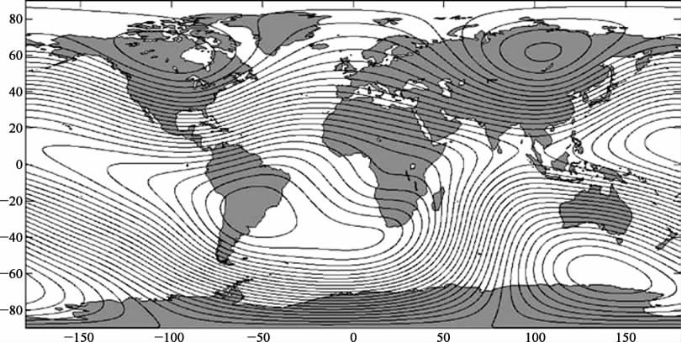
图16.3 地磁传输线来自IGRF 2005（表面）
一个特定的场模型是指其名字包含年代信息或者子代信息。此外，还存在一些确定的系数集，但并不打算对它们进行进一步的修改。最新出版的是IGRF2005（OGRF）集，其包括从1945—2000年确定的系数集和2005年初步设计的系数集，还包括从2005—2010年推断的系数集。网址为http：／／www.ngdc.noaa.gov／IAGA／vmod／igrf.html的网站上有更多关于IGRF模型的信息。
2）磁场计算
将坐标系设置在地球中心，可以很方便地计算磁场。因此，可以通过把磁场写成球谐函数求和的形式来实现这个计算过程，具体公式如式（16.3）所示：
在上述的方程中，向量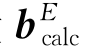
是以ECF为参考框架计算得出磁场，bn，m是维数为n和阶数为m的球面谐波。bn，m的组成部分如式（16.4）所示：
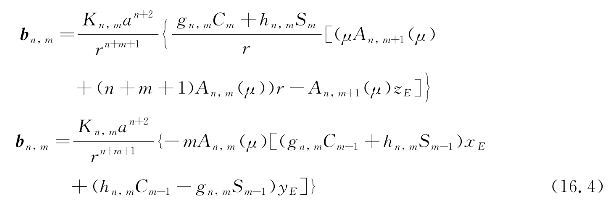
参数gn，m和hn，m是维数为n，阶数为m的高斯系数，由IGRF发布。参数a是地球的平均半径，等于6 371.2 km。参数r仅仅表示r的幅度，所要计算的位置在ECF参考框架里。单位向量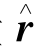
与r向量方向一致。参数μ是
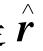的第三个组成部分，如式（16.5）所示：
(www.xing528.com)
式（16.4）中的剩余项可以通过递归方式求出来，具体公式如下所示：
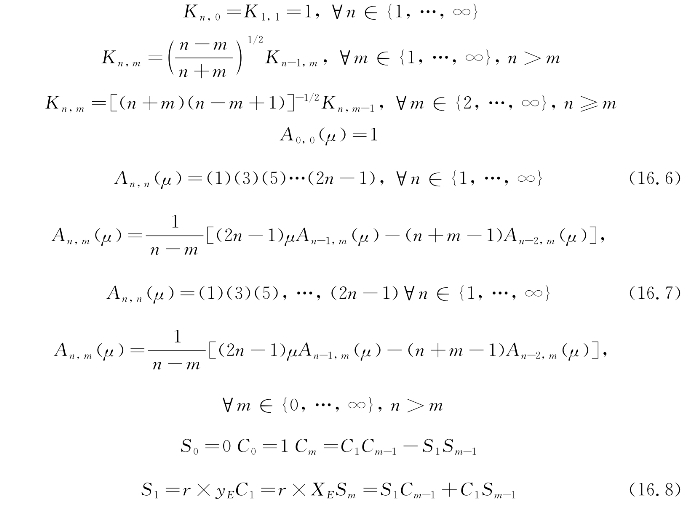
Kn，m被称为施密特系数，而An，m是由勒让德多项式推导出来的。虽然Sm和Cn是施密特相关系数，但把它们分离出来只是作为简化递归方程的一种手段。施密特系数与期望的位置无关。因此，有许多点分布在磁场中，如果要计算这些点的磁场，那么只需要计算一次施密特系数，而且该计算结果在后面的计算中可以重复使用。然而，其余的系数是位置相关的，而且还必须重新计算期望位置相关的系数。
3）模型的精度
为了确保IGRF反映高质量数据的精确性，在2001年，IAGA决定将2000年以后的IGRF主磁场系数的最大维数nmax扩展到13，引用精度为0.1 nT。2000年以前的主磁场系数扩展到8维或10维度，引用精度为1 nT。对于未来五年，用于长期预测的新变量系数的维数为8，精度为0.1 nT／年。
为了验证上述算法的精确性，用多个nmax的值计算磁场，并与通过STK软件仿真的得到的结果比较，该仿真采用十三阶求和的方法来实现。仿真结果如图16.4所示，从仿真图可以看出均方误差随阶数n的变化关系。当仿真阶数为10时，精度基本上无法进一步提高。
精度的提高是以增加计算时间为代价的，如图16.5所示。由于大多数ADCS的计算是在地面上完成的，可以提高精度。因此ION的所有计算使用阶数等于13的第十代OGRF模型。
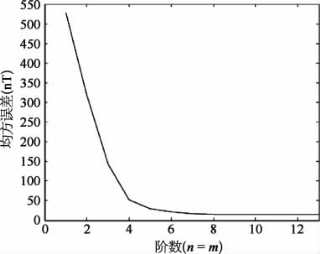
图16.4 均方误差与阶数的关系
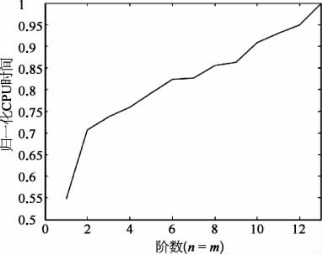
图16.5 归一化CPU时间与阶数的关系
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
