轨道计算通常是已知卫星在给定时刻的位置和速度或等价的轨道参数,然后来预测在期望时刻的这些参数值。通过开普勒第二定律将真近点角f和偏近点角E联系起来,这个过程将被大大简化。开普勒第二定律如下所示:
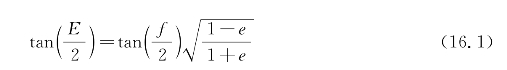
而且,可以进一步找出所经过的时间与偏近点角的关系,如下所示:
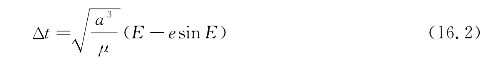
式中 Δt——从上次经过近地点后所经历的时间;
e——偏心率;
a——半长轴;
μ——万有引力常数。(https://www.xing528.com)
其中,在地球轨道时μ等于3.986×105km3/s2。
图16.1显示了典型的轨道计算逻辑框图。一旦轨道信息给定,例如位置和速度矢量,则第一步包含了这些向量转换为轨道参数的信息。此步骤仅显示了完整性但并不是必要的,因为TLE提供了一套独立的信息。接下来利用式(16.1),将初始时刻的真近点角转换为偏近点角E0。然后使用式(16.2)可以计算出时间Δt0,Δt0表示的是从上次经过近地点后所经历的时间。时间t0用于计算经过近地点的时间tp,如下图16.1所示。这个结果与期望时刻td一起用来计算Δtd,Δtd表示从上一次经过近地点至期望时刻所经历的时间。通过求解方程式(16.2)就可以逆向推导前述过程,并且可计算出期望时刻的偏近点角Ed。然后我们就可以用式(16.1)将Ed转换成期望时刻的真近点角。
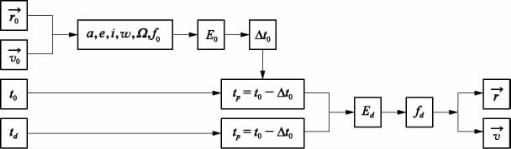
图16.1 轨道计算算法逻辑框图
为了尽量减少与姿态计算相关的计算负担,于是假设一个简单的两体引力模型。因此,地球扁率、太阳、月球及其他第三体摄动的影响都被忽略了。尽管如此,这种假设证明了预期计算的时间是非常准确的。图16.2展示了通过两体模型获得的地球中心惯性位置矢量和使用STK中高精度的(HPOP)得到的位置矢量的区别。这个特定的仿真连续运行24 h所产生的误差,在幅值上大约为7 km。虽然这个误差看起来比较大,但位置误差的大小对磁场的轻微影响在后面会说明。而且,开发上述轨道计算器是为了简化对姿态确定与控制子系统的开发及测试。即便该两体假设不准确,仍然有很多SKT仿真,可以高精度地计算ION位置。另外,摄动效应应补充到现有的轨道计算算法上。
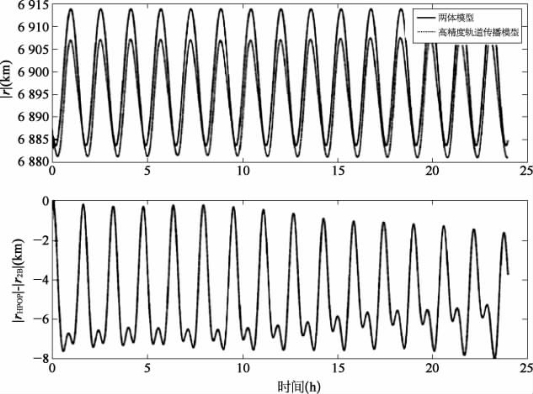
图16.2 两体模型下计算位置向量的精度
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




