假设没有多径或多普勒损耗，在接收器处观察到的窄带信噪比（SNR）如下：
其中b是接收机带宽和信号电平，路径损耗和噪声项已经根据Stojanovic的公式（14.3），取信噪比的频率相关部分，即路径损耗Path Loss（r，f，d，t）∑Noise（f，w，s）的积。由于信噪比与路径损耗Path Loss（r，f，d，t）∑Noise（f，w，s）因子成反比，因此对于
项，图14.9a为较长范围，而图14.9b为较短范围。这些图中的第一个显示了使用thorps吸收模型（球形扩展）长达10 km的各种范围，并由几位作者介绍。图14.9b突出显示了500 m和100 m的较短范围，并说明了第14.2.2.2节中开发的Thorp、Fisher和Simmons吸收损耗模型之间的变化。
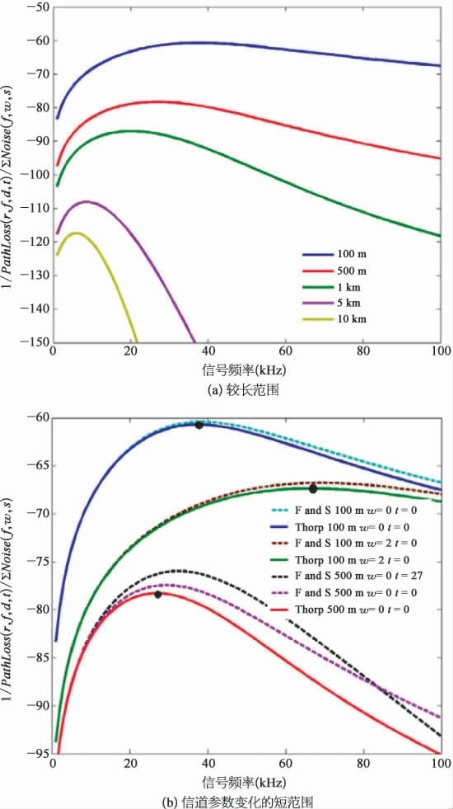
图14.9 窄带信噪比的频变分量
这些数字表明，假设投影机参数（包括发射机功率和投影机效率）在频带上的行为一致，那么存在一个信号频率，在该频率下，信噪比的频率相关分量是最优的。根据索普吸收模型，三条曲线顶点的黑点表明了这一最佳点。两种吸收模型的响应和最佳频率相似。在100 m处，最佳频率存在微小变化，其中吸收系数的贡献明显较低。在100 m范围内，当风的速度从0变为2 m／s时，环境噪声分量对最佳信号频率的影响最为显著，最佳信号频率从38 kHz变为68 kHz。(www.xing528.com)
从通信的角度来看，如果两辆车在100 m和38 kHz的速度下运行，并且风状态从0 m／s变为2 m／s，则信噪比的频率相关分量会减少9 dB。由于投影机参数的不同，这并不是信噪比的绝对降低，尤其是发射机功率水平没有被考虑。然而，它确实表明了风和波作用对水下数据通信的重大影响，此外，这种降低的信噪比值不包括与波作用产生的增加散射相关的任何增加的损耗。在环境噪声项中发现的运输影响不包括在这里，因为它对高于10 kHz的信号频率的影响很小。在第14.2.2.2节图14.4中，温度变化对与相关范围相关的信号频率影响最大。图14.9b说明了在信噪比的频率相关分量方面的差异。图14.10a进一步探讨了信号频率在范围内的变化。
如果航行器从100 m移动到500 m（风速为0m／s），保持最高信噪比的最佳信号频率从38 kHz下降到28 kHz，则可以看到范围变化的影响，如图14.9b。信号频率的降低意味着绝对带宽的潜在降低，以及需要管理的数据速率的降低。这将在下一小节中进一步研究。图14.10a和图14.10b显示了在Thorp、Fisher和Simmons吸收损耗模型中，各种参数、温度和深度以及环境噪声模型中的风的最佳信号频率变化范围高达500 m。最佳频率随吸收损耗的控制特性而增大。从图14.10a可以看出，随着范围的增大，两个模型之间以及Fisher和Simmons模型内的参数之间的偏差也越来越大。当温度升高时，500 m和6 kHz时，模型之间的差异约为2.5 kHz。当包括风时，如图14.10b，在非常短的范围内，最佳信号频率会发生剧烈变化，在所示的范围内，这种差异会大大减小。这是因为相对于恒定的环境噪声项（因为它不依赖于范围），吸收损耗项的重要性越来越大，这减少了噪声项的影响，因此也减少了风的参数。在图14.10a和14.10b中，Fisher和Simmons模型提供了更高的最佳频率，因为更准确地包含了硼酸和硫酸镁的弛豫频率。
图14.10 由窄带信噪比的频率相关分量确定最佳频率
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
