信号衰减及海洋智能无人系统技术

海洋中的声音传播受到海水的物理和化学特性以及信道本身的几何形状的影响。水下声信号由于扩散和吸收而经历衰减。此外，根据信道几何形状，水听器可能会经历多径衰落。路径损耗是从投影仪到水听器的信号强度损失的量度。理解和建立精确的路径损耗模型对于信噪比（SNR）的计算至关重要。

14.2.2.1　传播损耗

扩散损耗是由于声音信号所包含的扩展区域，因为它几何上从源向外扩散：

PLspreading（r）=k×10log（r）（dB）

式中　r——以米为单位的范围；

k——扩散因子。

当发生信号传输的介质是无界时，扩展是球形的并且扩展因子k=2，而在有界扩展中，被认为是圆柱形k=1。URick提出，球形扩散是海洋中的一种罕见的现象，但在短的范围内被认为是存在的。由于AUV编队操作将在短距离发生，因此可能需要考虑球面扩展，这意味着更高的衰减值。扩散损耗与覆盖范围成对数关系，并且其对信号的影响在非常短的范围内较显著，直到大约50 m，如图14.5a所示。在这些较短的范围内，与吸收项（与范围具有线性关系）相比，扩散损耗成比例地增大。

14.2.2.2　吸收损耗

吸收损耗表示由于声信号产生的波向外传播时发生的黏性摩擦和离子弛豫引起的热量形式的能量损耗，并且该损耗随着如下范围线性变化：

PLabsorption（r，f）=10log（α（f））×r（dB）

式中　r——以千米为单位的范围；

α——吸收系数。

更具体地说，海水中的声音吸收是由三种主要影响引起的：黏度（剪切和体积），硼酸和硫酸镁（MgSO4）分子的离子松弛和弛豫时间。在100 kHz以上的高频率下黏度的影响是显著的，而镁的离子松弛效应影响10～100 kHz的中频范围和低至几千赫兹的低频率的硼酸。通常，吸收系数α随着频率的增加而增加，随着深度的增加而减小，与淡水相比，由于离子弛豫因子的影响，海水中的离子浓度明显高于淡水。

在过去的半个世纪中，对吸收损耗的广泛测量已经产生了几个经验公式，其考虑了频率、盐度、温度、pH、深度和声速。一个流行的版本是Thorp的表达式，等式（14.1），它基于Thorp在60年代的初步研究，并且已经转换为公制单位。它适用于100 Hz至1 MHz的频率，基于盐度为35%ppt，pH为8，温度为4℃，深度为0 m（大气压力）的海水，这是假设但未由Thorp说明：(www.xing528.com)

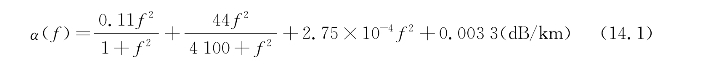
Fisher和Simmons已经提出了α的其他变体。特别是70年代后期的Fisher和Simmons发现了与硼酸在吸收上的松弛相关的效应，并提供了更详细的吸收系数α形式，以dB／km为单位，随频率、压力（深度）和温度而变化（也有效）对于100 Hz至1 MHz，盐度为35%ppt，pH为8，由公式（14.2）描述：

式中　d——以m为单位的深度；

t——以℃为单位的温度；

“A”系数——温度的影响；

“P”系数——海洋深度（压力）；

f1，f2——硼酸和（MgSO4）分子的弛豫频率。这些术语由Fisher和Simmons提出。

图14.4显示了Thorp、Fisher和Simmons系数的dB／km与信号频率的吸收系数，并显示α在一般固定温度和深度下随着频率的增加而增加。直到80 kHz左右，温度变化对α的影响比深度更明显，但在这些频率之上，深度开始占主导地位。无论如何，Thorps的近似值与Fisher和Simmons非常接近，并且在显示的频率上显然更加保守。Sehgal表明，在300 kHz以上的较高频率下，Thorps模型预测损耗较低，因为它没有考虑Fisher和Simmons发现的弛豫频率。如果深度和频率固定且温度在0～27℃之间变化，则对于30～60 kHz范围内的频率，α的降低约为4 dB／km，这与Urick提出的结论相关。如果考虑AUV编队最有可能在哪里运行，那么在“混合表面层”中，由于纬度（平均温度为17℃，温度变化很大），温度可能是一个重要因素。应该注意的是，如果在较低温度下操作α较高，因此使用0℃将是一种保守的替代方案。

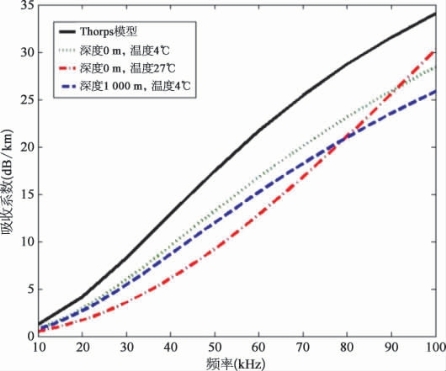
图14.4　吸收系数与频率的关系

如上所述，在这些较低频率下，深度（压力）对α的影响小于温度。Domingo研究了深度（压力）对吸收的影响，并证实了对于低于100 kHz的较低频率，α的变化较小。更具体地说，Urick将变化定义为：αd=α×10-3（1-5.9×10-6）×d（dB／m）（其中d为以m为单位的深度），但也建议近似为2%每300 m深度减少。因此，深度（压力）变化预计不会在短距离AUV编队操作中发挥重要作用，尤其是使用本章所述的2D水平拓扑的编队。