海洋智能无人系统技术：控制信号调节

通过评估式（12.2）得到的fi（k）←E[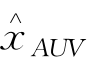（k）］的解，或更准确地说式（12.29），由SP-UKF提出的估计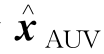（k），将用于形成由式（12.41）、式（12.44）中的前进速度和航向控制器接受的命令，c=［］。

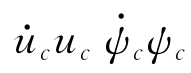AUV的低级控制系统的任务是尝试重建将f（k）应用于无约束点单位质量即完整2D二元积分器模型的运动，直到推力分配、运动学和实际航行器的动态约束。在以下等式中，以欧拉反向公式的形式假设在R2空间上的积分的时间T的采样。则自然地：

其中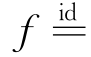‖f‖是总控制力的范数，允许分解为［f‖f⊥］T，与AUV航向方向平行且垂直的分量。由ψ（k-1）给出，尽管可能由x2=v2=v≠0得到的侧滑。

此时，假设AUV具有指定的性能包络。

利用这些作为给定的独立参数，式（12.81）～式（12.84）的操纵导致约束，其规定f需要被钳位的可允许范围，以避免迫使AUV的低电平控制器超出其正常操作范围。

1）约束不等式

根据式（12.81）得出的f的解的轨迹更易于在AUV固定坐标系中可视化［一个原点为xi，x轴与u（k-1）∠ψ（k-1）对齐］。其中，允许的解决方案轨迹是沿x轴的偏移量u（k-1）／T，由隐式表达式给出：(www.xing528.com)

类似于前述情况，式（12.82）的解决方案的轨迹是与式（12.85）描述的盘同心的偏移环带：

式（12.83）的解的轨迹与前一种情况类似，是式（12.86）所述的以圆盘为中心的偏置环空：

式（12.84）的解的轨迹同样是与所有其他轨迹同心的无限圆盘（1锥）的角扇区，其满足不等式：

如果f（k）满足式（12.85）～式（12.88）中所述的所有标准，即它是否属于R2形状为环形扇区的子集，则f（k）的解是合法的。

2）逼近总控制力

如果式（12.85）～式（12.88）不满足，则采用非线性程序将f收紧到允许范围内。因此，低级控制器的操作点保持在滑动面的准线性附近。该程序在算法3中是伪编码的，用该算法逼近后，用式（12.81）～式（12.84）生成命令c=［acucrcψc］T作为底层命令用于低阶控制器。