转子矫正技术在海洋智能无人系统中的应用

由于虚拟势的制导方法极易受到局部最小值的影响，需要一种强大而简单的方法来确保避免局部最小值。

就式（12.2）引入的矢量场而言，其解析解在式（12.20）和式（12.21）中给出，由于场的非旋转性而发生稳定的局部最小值，E（x）=id0。

为了避免非旋转性，从而避免局部最小值，重新设计了式（12.7）、式（12.10）和式（12.12）中提出的分散控制功能，增加了转子部件：

其中a′i是重新定义的总分散控制功能，指第i个特征（以下将省略破折号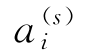）；是前一节中介绍的定子分散控制功能，用上标表示，以与新引入的形成对比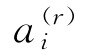；是转子分散控制函数，所有这些都是欧几里得2空间上的连续实际2D矢量场（将R2映射到自身），使得它们在每个定义的任何地方都存在雅可比行列式。

引入通过设计建立非零rot（E），如下：

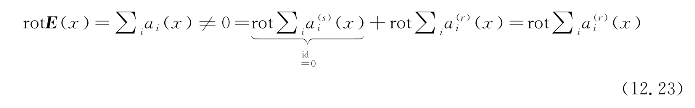
对于航路点，在此框架下，航路点对AUV的潜在影响不应因渐近方向而受到影响。如果使用转子部件增加了航路点的分散控制功能，则aw的方向将偏离视线。形成单元顶点也是如此。因此，唯一的非零转子分散控制功能是障碍。因此，式（12.23）可以进一步简化为：

(www.xing528.com)

单个障碍物转子分散控制功能定义如下：

i=enum（obstacles）

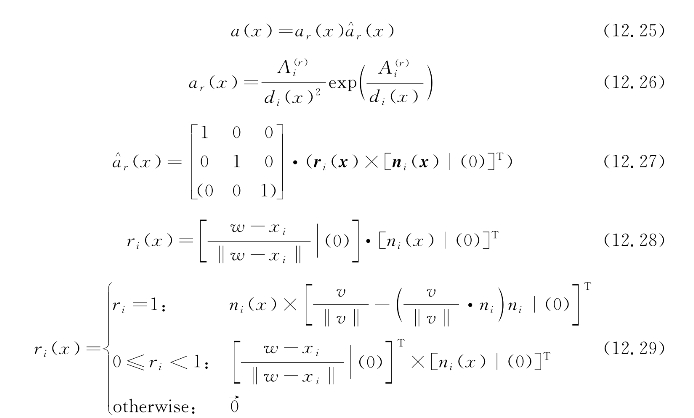
式中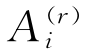∈R＼｛0｝——一个正的真实独立参数，指示垂直于障碍物最快飞行方向的加速度标度；

v∈R2——当前AUV真实的水面速度（包括可能的侧滑）投射到“航高上限”上。转子分散控制功能和由转子和定子部件叠加组成的总分散控制功能如图12.6所示。

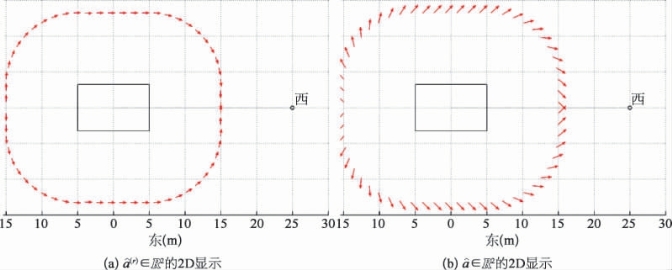
图12.6　转子分散控制函数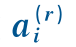的方向和两项ai=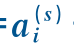+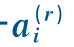分散控制函数