海洋智能无人系统技术：势轮廓生成器与分散控制功能

至于势轮廓生成器pi（d）：→R，它们的定义遵循指导AUV的全局目标。考虑到这些，每个特征类型的势轮廓生成器p（o，w，c）（障碍物、路径点和阵型单元顶点）被指定。如图12.3所示。

图12.3　障碍物的势轮廓生成器po［d（x）］

1）障碍

其中，po（d）：R+→R是障碍物的势轮廓生成器，严格单调递减的平滑单值Lebesgue可积函数将非负实数映射到实数；A+∈R+＼｛0｝是一个正的真实独立参数，指示远离障碍物的加速度的大小。

2）航路点

其中，pw（d）：R+→R是路点的势轮廓生成器，严格单调递增的平滑单值Lebesgue可积函数，将非负实数映射到实数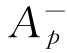；∈R+＼｛0｝是一个正的真实独立参数，指示朝向比例吸引区域中的路点的加速度；∈R+＼｛0｝是一个正的真实独立参数，指示朝向该方式的恒定加速度在比例吸引区域之外的点；dp∈R+＼｛0｝是一个正的真实独立参数，用于指示以构成比例加速区域的路点为中心的开放球的半径。如图12.4所示。

图12.4　路点pw［d（x）］的势轮廓生成器

3）单元顶点(www.xing528.com)

形成单元顶点的良好候选势轮廓生成器（其行为类似于具有局部支撑的函数）是正态分布曲线，针对吸引力（即反转符号）进行调整。

其中，pc（d）：R+→R是阵型特征单元格的顶点的势轮廓生成器，严格单调增加的平滑单值Lebesgue可积函数，将非负实数映射到实数；∈R+＼｛0｝是一个正的真实独立参数，指示在朝向顶点的最大加速度距离处朝向单元顶点的加速度［相当于高斯的·N（±σ）的估值正态分布曲线］；dc∈R+＼｛0｝是一个正的真实独立参数，用于指示势轮廓生成器中出现拐点的球体半径，即朝向顶点的最大加速度发生的距离［取式（12.12）中σ的位置，类似于高斯正态分布曲线］。

图12.5　构造agent的势轮廓生成器

围绕着作为障碍物的正方形单元的势如图12.5所示。

4）分散控制重新制导

式（12.6）、式（12.8）和式（12.11）的单调性确保了势的梯度方向（x）／‖（x）‖∈SO2总是±ni=（x-xi）／‖x-xi‖。因此，由于式（12.1）和式（12.2）是线性的，式（12.2）可以解析地求解由式（12.6）、式（12.8）和式（12.11）指定的形式的任何有限和项，直到独立参数的值（A+，，dc）。程序如下：

可以通过将式（12.7）、式（12.10）和式（12.12）中的项分别指定为a（o，w，c）来概括等式（12.18）。术语·ni，同样可以分别表示为，并表示由于第i个特征，基于势的分散控制功能。