海洋智能无人系统技术：实时最优制导

对于图11.2和图11.3所示的动态轨迹发生器，建议使用基于直接法的IDVD。基本原理是这种方法具有实时实现所需的几个重要特性：①预先满足包括高阶导数在内的边界条件；②得到的控制命令平滑且物理上可实现；③该方法非常稳健并且对输入参数的微小变化不敏感；④优化过程中可以使用任何复合性能指标。此外，该方法只使用了少量的变量参数，从而保证了优化过程中的迭代过程与其他直接方法相比收敛得更快。基于IDVD的轨迹发生器由几个模块组成。接下来要讨论的第一个模块的目标是生成一个满足边界条件的候选轨迹。

1）生成候选轨迹

同样，考虑AUV在3D中运行的最一般情况（与USV相反）。假设候选AUV轨迹的每个坐标xi，i=1，2，3表示为某个抽象参数τ的M次多项式，表示为式（11.9）。

为了简化符号，假设x1（τ）≡x（τ），x2（τ）≡y（τ），x3（τ）≡z（τ）。一般来说，轨迹坐标的解析表达式可以由任意基函数组合而成，以产生丰富多样的候选轨迹。例如，使用单项式和三角函数的组合。M由必须满足的边界条件数量决定。具体来说，它应该大于或等于预设边界条件的个数而不是一个。一般来说，所需的轨迹包括对初始位置和最终位置、速度和加速度的约束：xi0，xif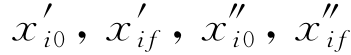，。在这种情况下，式（11.9）的最小阶数是5，因为其中所有系数都将由这些边界条件唯一定义，而长度τf将是唯一可变的参数。为了在候选轨迹中获得更大的灵活性，可以通过增加式（11.9）的阶数来获得更多的可变参数。例如，使用7阶多项式将为每个坐标表达式引入两个不同的参数。在这些扩展多项式中，不直接改变两个系数，而是分别改变初始加加速度和最终加加速度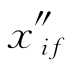，。在这种情况下，式（11.9）中的系数aik可通过求解明显的线性代数方程组来确定，该方程组在两个端点（τ=0和τ=τf）将多项式（11.9）等同于xi0，xif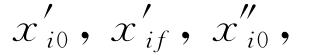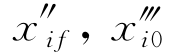，和。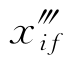

通过构造，最终弧τf的任何值都将无条件满足边界条件式（11.5）。然而，改变τf将改变候选轨迹的形状。图11.4展示了一个简单的例子，即一个以1.5 m／s的速度在海床以上2 m处运行的AUV必须执行一个弹出操作以避免一些障碍物。即使只有一个变化的参数，改变τf的值也能使AUV避开不同高度的障碍物。类似的轨迹可能只在水平面或所有三维空间中产生。应该指出的是，即使在这个阶段，不可行的候选轨迹将被排除在外［在图11.4中，要求AUV跳出水面的轨迹是不可行的，因为它违反了约束条件式（11.6）］。

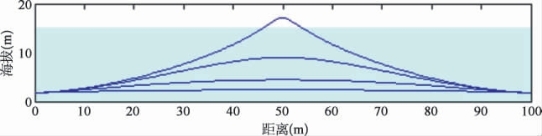
图11.4　改变τf时改变候选轨迹的形状

在该例子中，有6个自由参数是初始加加速度和最终加加速度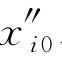（和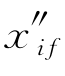，i=1，2，3）的组成部分，轨迹生成器可以进一步改变轨迹的整体形状。为此，图11.5表明了AUV避开初始点和最终点之间10 m障碍物的候选轨迹。这些轨迹是通过改变加速度的两个分量和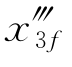和最小化τf产生的。这种附加的灵活性可以产生满足操作约束式（11.6）和OA约束式（11.7）的轨迹。

图11.5　改变终点加加速度获得的候选轨迹

特定轨迹的选择将基于轨迹是否可行［满足约束式（11.8）］，如果可行，则确定是否确保性能指数为最小值，该值是使用沿该轨迹的航行器状态（和控制）值计算得出的。作为一个例子，图11.6给出了1个10 m高障碍物的两个不同位置的无碰撞解决方案，其中5个参数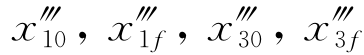和τf经过优化以确保可行的最小路径长度轨迹。

图11.6　最小路径长度轨迹的示例

现在，讨论选择一些抽象参数τ作为参考函数式（11.9）的参数而不是使用常用的时间或路径长度的原因。暂时假设τ≡t。在这种情况下，一旦确定了轨道，也就明确地定义了沿着该轨迹的速度曲线，因为

利用抽象参数τ，通过引入速度系数λ使独立地改变速度曲线成为可能

现在代替式（11.10）有

通过改变λ（τ）可以实现任何所需要的速度曲线。

在轨道终点，特别是在初始点，满足高阶导数的能力允许轨迹的连续再生以适应突然的变化，如新发现的障碍物。作为示例，图11.7展示了一种情况，执行OA操纵的AUV发现第二个障碍物并且必须从当前航行状态和控制值（到状态的二阶导数）开始生成一个新的轨迹。提出的方法可以实现这种类型的连续轨迹生成，并确保平稳、无冲击过渡。

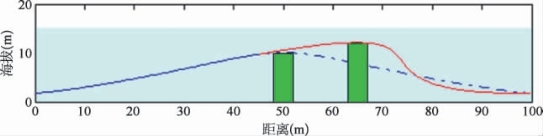
图11.7　动态轨迹重新配置的示例

2）逆动力学

图11.2和图11.3中动态轨迹生成器内的第二个键块接受候选轨迹作为输入，并计算状态向量的分量和跟踪它所需的控制信号。这样，可以确保每个候选轨迹不会违反任何约束［包括式（11.8）中的约束］。

首先，对任意参数ζ使用下列关系

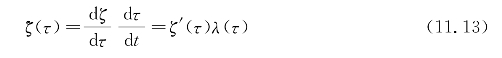
这里将运动方程式（11.2）转换为τ域

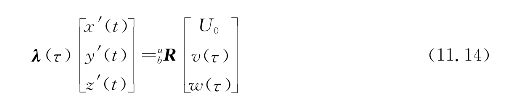
接下来假设俯仰角足够小使sinθ（t）≈0和cosθ（t）≈1，所以旋转矩阵（11.3）变为

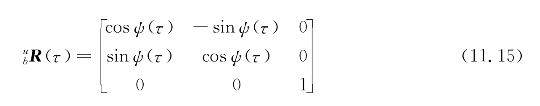
虽然不需要此步骤，但它简化了以下的表达式。通过旋转矩阵（11.15）反转矩阵（11.14）得到

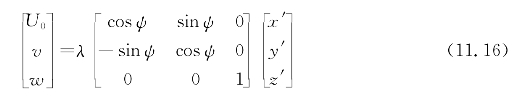(www.xing528.com)

此后，符号中将省略每个变量对τ的显式依赖。现在必须根据三个未知参数v，w和ψ来解式（11.16）的三个方程。以后每个变量的显式依赖τ将省略符号。现在，式（11.16）的三个方程必须根据三个未知参数v、w和ψ来求解。而最后一个很容易得到式（11.17）。

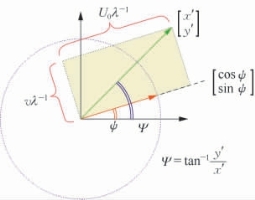
图11.8　水平面参数运动学

前两个需要更严格的分析。

参考图11.8，几何上，式（11.16）中第一个等式右边的两个矢量的标量积表示阴影矩形最长边的长度。同样，第二个等式表示这个矩形最短边的长度。从这里可以看出，对角线向量长度的平方可以用两种方式表示：。这就产生了式（11.18）：

从同一个图形可以看出

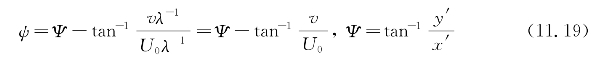
现在，使用这些逆动方程，可以检查每个候选轨迹是否服从加于它的约束［约束式（11.8）］。

3）离散

继续沿参考轨道在一组固定的N个点（例如，N=100）上计算剩余状态，这些点沿虚拟弧［0；τf］均匀分布，间隔为

以便

为了确定多项式（11.9）的系数，必须猜测变量τf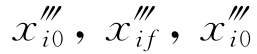，和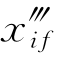的值。这些猜测将与已知或期望的边界条件xi0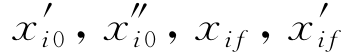，和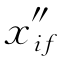一起使用。坐标xi0和xif的边界条件直接来自式（11.5）。根据式（11.14）给定的纵荡、横荡和垂荡速度边界条件将坐标的一阶时间导数定义为

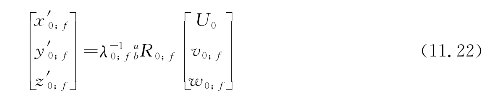
它们还定义了用于计算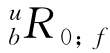的初始和最终纵摇角和首摇角，在式（11.22）中为

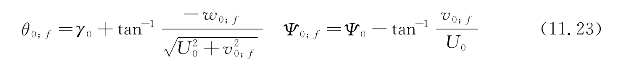
在方程式（11.22）中，可以使用初始和最终速度系数λ的任意值，例如，λ0；f=1。该值仅缩放虚拟域；λ的值越高，τf的值越大。这直接从方程式（11.11）和式（11.12）得出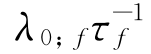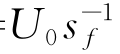：=，其中sf是物理路径长度。

最后，二阶导数的初始值由AUV运动传感器提供（转换为τ域后），而二阶导数的最终值通常设置为零，以便平稳到达最终点。具有候选轨迹条件式的分析表述定义了xij和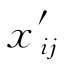的值，其中i=1，2，3，j=1，2，…，N。

现在为每个节点j=1，2，…，N计算

其中

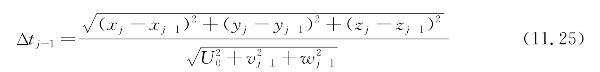
然后用式（11.17）～式（11.19）计算每个时间戳的v、w和ψ。垂直平面参数，航行路径角γ和俯仰角θ可以使用式（11.26）关系计算。

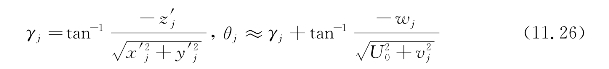
为了检查约束式（11.8）中的首摇率，必须首先在数值上区分式（11.19）的Ψ的表达式。

4）优化

当所有参数（状态和控制）都在N个点上计算时，可以计算性能指标J和惩罚函数。例如，可以将约束式（11.6）和式（11.8）结合到联合惩罚中，表示为式（11.27）。

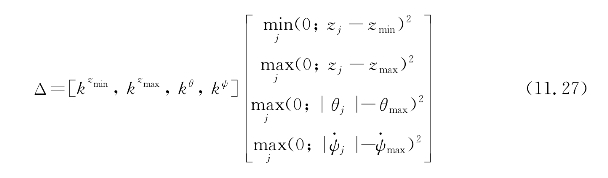
其中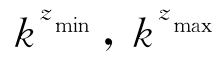，，kθ和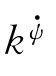为比例（加权）系数。在Matlab开发环境中，利用内置的fmincon函数等数值方法可以解决这个问题。或者，通过将性能指标J与联合惩罚Δ相结合，可以利用Matlab的非梯度fminsearch函数。然而，对于实时应用，作者更喜欢使用基于无梯度Hooke-Jeeves模式搜索算法的更健壮的优化例程。