海洋智能无人系统技术中的AUV动力学方程

考虑最一般的情况，并介绍一个计算三维无碰撞轨迹的优化问题（通过消除两种状态，可以将其简化为二维问题）。这里将在状态向量描述的一组可接受的轨迹内进行搜索，如式（11.1）所示。

其中速度矢量的分量，在主体框架｛b｝中定义的纵荡u、横荡v和垂荡w被添加到AUV-NED的坐标x、y和z中（表面为z=0，并随深度增加）。虽然许多AUV通常被设定为在高于海底的恒定高度上运行，但更可取的方法是在NED局部切面中生成垂直轨迹，因为水面是比可能不平坦的海底更可靠的绝对参考基准。然而，一般来说，对于配备高度和深度传感器的航行器，将产生的深度轨迹z（t）转换为高度轨迹h（t）是一件微不足道的事情。

可容许轨迹应满足描述AUV运动学的常微分方程组：

在公式（11.2）中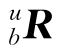，是从主体框架｛b｝到NED框架｛u｝的旋转矩阵，使用两个欧拉角俯仰角θ（t）和横摆角ψ（t）定义，忽略横摇角，如式（11.3）所示。

虽然不打算在这项研究中利用它，但是可容许轨迹也应该遵循描述平移和旋转运动的AUV动力学方程。这意味着下面的线性化系统适用于矢量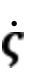（t），表示为式（11.4），其中包括速度分量u，v，w［作为状态矢量z（t）的一部分］和角速率p，q，r。

这里A和B为状态矩阵和控制矩阵，δ=［δT，δs，δr］T是控制向量。

接下来可容许轨迹式（11.1）应满足初始和终止条件式（11.5）。(www.xing528.com)

最后，状态变量、控制变量及其导数应遵循一定的约束条件。例如，在AUV下这些可能包括对AUV深度的明显限制，如式（11.6）。

其中，zmax（x，y）表示设定操作深度限制。对于设定为在海床以上某个名义高度上运行的航行器，zmax（x，y）约束可转换为前文所述的最低高度hmin（x，y）约束。

一个三维的OA要求可表述为式（11.7）。

其中，R是所有已知障碍物位置的集合。约束通常不仅施加在控制器本身|δ|≤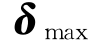上，而且也施加在它们的时间导数||≤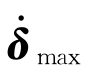上解释执行器动态。知道系统的动态见式11.4（或简单地遵守自动驾驶仪的规范），后面提到的约束可以提升到参考信号的水平，例如式（11.8）。

其目标是找到最佳轨迹和相应的控制输入，以最小化某些性能指标J。典型的性能指标规范包括：①最小化操纵时间tf-t0；②最小化行驶距离以避免障碍物；③最小化控制工作量或能量消耗。此外，性能指数可能包括一些由传感器有效载荷决定的“外来”约束。例如AUV可能需要航行轨迹，其将固定的FLS指向特定地形特征或将航行器俯仰运动至最低保持水平，保持沿测量轨道线的水平航行来获得准确的合成孔径声呐图像。

在继续实施控制算法之前，需要注意的是，通常认为AUV的纵荡速度是恒定的，即u（t）≡U0，以便在另外两个通道中提供足够的控制权限。这唯一地定义了油门设置δT（t），只留下两个控制输入δs（t）和δr（t），用于改变航行的轨迹。它还允许将式（11.4）中的矩阵A和B视为常量（与时间和状态无关）。如果不需要这一假设，反向运动学和动力学方程将与下一节中给出的示例略有不同。