海洋智能无人系统技术：控制准则设计与分析

在深入研究特定控制系统如何产生校正信号的规律之前，有必要了解AUV内各种系统的需求。这将更好理解控制系统如何适应AUV的总体自治体系结构。需要关注不同类型的扰动并使得这些扰动的影响最小化，以及分析与航行器动力学运动有关的方程。只有考察了这些因素，才能对控制准则进行设计和分析。

1）需求

如前所述，构成AUV自治体系结构的各种组件包括导航系统、航行系统和控制系统。这三个系统有各自单独的任务要完成，但也必须协同工作，以使航行器可靠地完成任务。图10.6是这些不同系统的交互框图。

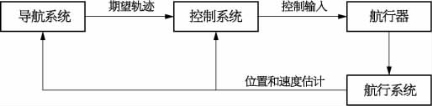
图10.6　导航、航行和控制框图

导航系统负责生成航行器需要遵循的轨迹。这项任务是根据航行任务前确定的所需航路点来完成的，并可能包括外部环境扰动的情况，为航行器生成一条路径，以便到达每一个连续的航路点。关于航行器当前状态的信息，例如制动器配置和可能的故障，也可为航行器提供要遵循的实际轨迹。然后该轨迹生成航行器的期望状态，包含期望的位置、方向、速度和加速度信息。

航行处理系统确定航行器当前任务的状态。对于地面、陆地和空中运载工具，GPS通常可用于向航行系统提供连续的精确定位信息。然而，由于这些信号在水中的传播极为有限，GPS在很大程度上无法用于水下航行器。航行系统的任务是基于多个从其他本体感受器和外部感受器的测量结果来计算航行器当前状态的最佳估计，并且只有在GPS可用时才使用GPS。这是通过使用某种形式的传感器融合技术来完成的，例如卡尔曼滤波或粒子滤波，以获得当前操作条件的最佳估计，并且在GPS可用时允许校正机制，例如当航行器浮出水面时。总体而言，航行系统的任务估计是无论可用的传感器信息是什么，都能为航行器提供当前状态的最佳估计。

2）控制

控制系统负责提供信号校正，以使航行器能够沿着期望路径行驶。这是通过从导航系统接收航行器的期望状态以及从航行系统接收航行器的当前状态来实现的。然后，控制系统通过在航行器上使用各种制动器来计算并施加校正力，以最小化期望状态和当前状态之间的差异。这使得航行器即使在存在未知扰动的情况下也能够跟踪期望的轨迹。即使上述每个系统负责它们各自的任务，它们也必须协同工作使水下航行器充分实现自治。

3）环境

水下环境可能极其复杂并且高度动态，使得AUV的控制成为一项极具挑战性的任务。必须对海流和波浪等的扰动进行处理，才能使AUV克服这种环境扰动。

海流是水的大规模运动，是由多种来源引起的。存在于海洋上层的海流的一个组成部分是由于海面上的大气风条件造成的。盐度水平的变化和海洋表面的热量交换的共同作用造成海水密度的不同，因此在海洋内存在着称为温盐流的额外水流。科氏力是地球绕其轴线旋转所产生的力，也会引起海流，而其他星球，如月球和太阳所产生的引力也会产生另一种影响的海流。将所有这些水流来源与孤立沿海地区存在的独特地理地形结合起来，导致世界海洋中存在着高度活跃和复杂的海流。

导致海洋中风生波浪形成的因素很多。风速，风吹过的区域，风影响海洋表面的持续时间和水深，这些只是导致风生波浪形成的一些因素。这些风生海洋波浪在海面上的振荡运动使得海面上的任何航行器都将经历同样的振荡扰动。此外，由于风生波浪运动，水下航行器在海面或近海面时将同时经受平移力和旋转力矩。

4）动力学

通过分析AUV的物理特性，可以推导出一组方程组，该方程组确定AUV通过诸如水类流体的运动。为了降低这些方程的复杂性，根据每个坐标系所具有的性质来使用特定的坐标系。为了将这些不同的坐标系用于不同的目的，必须进行从一个坐标系到另一个坐标系的转换。

在上文的控制系统中，使用的两个主要坐标系是N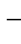坐标系和B坐标系。两者都包含三个平移分量和三个旋转分量，但两个坐标系的起点不同。这种起点上的差异可以产生有用的特性，这些特性在设计控制系统时具有一定的优势。

①N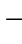坐标系。

N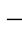坐标系是一个坐标空间，通常定义为一个平面，其方向与地球表面相切。水下航行器控制设计中最常见的坐标系是东北向下（NED）坐标系。顾名思义，这个坐标系的三个平移分量的轴包括指向北方的x轴、指向东方的y轴和垂直于地球表面向下方向的z轴。一般来说，航路点是参照地球上的一个固定点定义的，因此在此坐标系内进行导航和航行是方便的。

②B坐标系。

B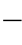坐标系，也称为体坐标系，是一个原点固定在航行器本体的运动参考坐标系。由于在航行器本体内不同点处存在各种性质，因此方便将该坐标系的原点放置在这些点之一处，例如利用物体对称性、重心或浮力中心。通常，该坐标系的x轴沿着本体的纵轴从后指向前，y轴从左舷到右舷，z轴从上到下。基于该坐标系的取向，在该坐标系中表示航行器的速度是合理的。

NED和体坐标系都具有对水下航行器控制设计有用的特性。由于两者的用途不同，需要将信息从一个坐标系转换到另一个坐标系。运动学方程式（10.3）实现了这一过程。

这里，式（10.3）在NED坐标系中进行分解，6自由度位置和方位向量由式（10.4）表示。

在式（10.4）中，三个位置分量由式（10.5）给出，

并且在式（10.6）中给出了三个方位分量，也称为欧拉角。

式（10.3）中的6自由度平移和旋转速度矢量在体坐标系中分解为式（10.7）。

这里，三个平移速度分量由式（10.8）给出，

三个转速分量由式（10.9）给出。

为了从一个坐标系旋转到另一个坐标系，在式（10.3）中使用变换矩阵。式（10.10）中给出这个变换矩阵。

这里，通过使用欧拉角式（10.6）旋转体坐标系式（10.8）中的平移速度来实现从体坐标系到NED坐标系的平移速度的转换。在该操作中使用三个主旋转矩阵，如式（10.11）所示。

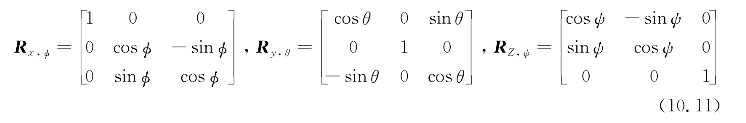
由于旋转顺序的复合效应，旋转顺序不是任意的。在导航和控制中，通常使用zyx约定，通过式（10.12）实现旋转。

总之，产生平移旋转矩阵（10.13）。

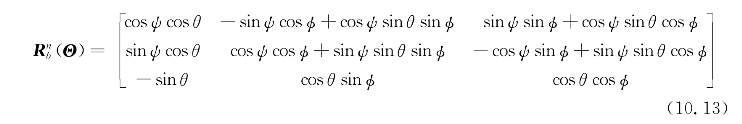
通过再次应用式（10.11）中的主旋转矩阵来实现从体坐标系到NED坐标系的旋转速度的变换。为了便于理解，首先考虑从NED坐标系到体坐标系的旋转，其中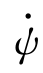通过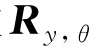旋转，并加到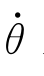上，然后它们的和通过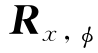旋转，最后加到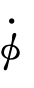上。该方法在式（10.14）中给出。

通过展开式（10.14），旋转速度从NED坐标系变换到体坐标系的矩阵定义为式（10.15），

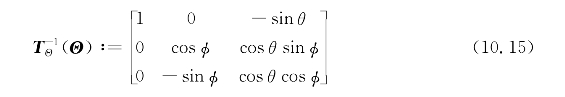
因此，在式（10.16）中给出了用于将旋转速度从体坐标系变换到NED坐标系的矩阵。

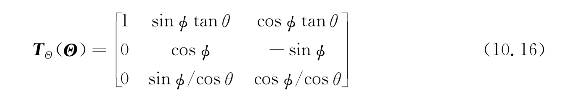
总之，式（10.3）实现从体坐标系到NED坐标系的旋转，并且通过取式（10.10）的倒数，可以实现从NED坐标系到体坐标系的旋转，如式（10.17）所示。

水下航行器的6自由度非线性动力学方程可以表示为式（10.18）。

这里，M表示包含刚体和附加质量的6×6系统惯性矩阵，如式（10.19）所示。

与式（10.19）相似，式（10.20）给出了包括附加质量在内的6×6科氏力和向心力矩阵。(www.xing528.com)

线性和非线性水动力阻尼包含在6×6矩阵D（v）中，由式（10.21）给出。

这里，D包含线性阻尼项，Dn（v）包含非线性阻尼项。

引力和浮力及力矩的6×1矢量在式（10.18）中用g（η）表示，并用式（10.22）定义。

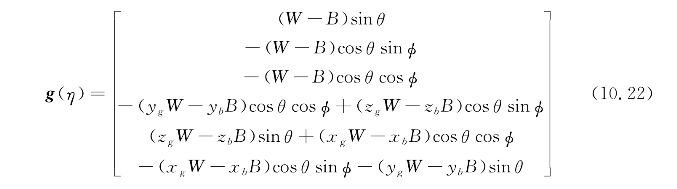
这里，W是航行器的重量，使用W=mg确定，其中m是航行器的干质量，g是由于重力引起的加速度。B是水下航行器的浮力，该浮力是由于水下航行器排水量所致。这将取决于航行器的大小和形状。确定重心和浮力中心相对于体坐标系原点的位置的矢量分别由式（10.23）和式（10.24）给出。

控制输入力的6×1向量用τ表示，由式（10.25）给出。

这里，影响纵荡、横荡和垂荡的平移力分别为X、Y和Z，而影响横摇、纵摇和首摇的转矩分别为K、M和N。

外部扰动的6×1矢量用ω表示。

总之，式（10.18）提供了水下航行器的非线性动力学运动方程的简洁表示，该运动方程在体坐标系中表达。通过施加包含在式（10.10）中的旋转，式（10.18）可以在NED坐标系中用公式（10.26）表示。

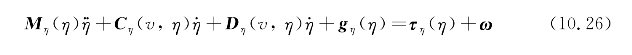
在式（10.26）内，等式（10.27）包含从体坐标系到NED坐标系的各种矩阵的旋转。

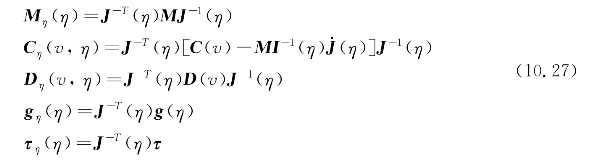
Dn（v）中含有非线性项，再加上所有矩阵中任何非零非对角元素的耦合效应，可以得到一个包含大量系数的高度复杂的模型。

5）控制准则

各种控制策略和控制准则，已经在AUV系统得到了实现。

控制系统的基准是经典的PID控制，它已成功地用于控制许多不同的对象，包括自主式航行器。然而，PID方案在强海浪和海流扰动的未知环境中处理具有不确定模型的非线性动力学问题不是很有效。因此，PID方案通常仅用于在没有任何外部干扰的环境中工作的非常简单的AUV。

滑模控制（sliding mode control，SMC）是变结构控制的一种形式，在处理具有建模不确定性和非线性扰动的非线性动力学问题上，已被证明是一种更为有效和鲁棒的控制方法。SMC是一种在保持良好稳态响应的同时，能够利用非线性开关项获得快速瞬态响应的非线性控制策略。因此，SMC一直在AUV领域得到广泛的应用。将SMC用于水下航行器控制的最早应用之一由Yoerger和Slotine实现，他们通过对ROV模型的仿真研究，证明了SMC控制器对参数不确定性的鲁棒性。Heley和Lienard提出了一种基于状态反馈的多变量滑模控制器，该控制器具有解耦设计，可独立控制水下航行器的速度、转向和俯冲。据Marco和Healey所述，该控制器的设计已成功地在NPSAriesAUV上实现。

PID控制的基本原理是产生误差信号，该误差信号将设备的期望状态与实际状态式10.28相关联，

式中　e（t）是误差信号；

xd（t）是设备的期望状态；

x（t）是设备的当前状态，并且操纵该误差信号以引入指示的校正动作τ（t）到设备。

之所以称为PID控制是因为组成校正控制信号的三个因子分别是与误差信号成比例的因子KP、与误差信号的成积分的因子KI和与误差信号成微分的因子KD为式（10.29）。

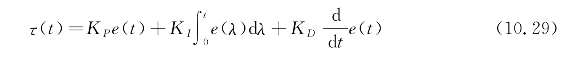
PID控制最适合于线性对象，但也已被用于非线性对象，尽管它缺乏与其他控制系统相同的性能水平。

然而，由于PID控制在控制各种线性和非线性对象被广泛接受和使用，因此它被大量地用作控制系统测量的“黄金标准”。Jalving给出了一个基于PID的水下航行器控制策略的例子。

如前所述，滑模控制是一种利用不连续切换项来抵消在控制器设计阶段未考虑的动力影响的方案。

为了研究如何将滑模控制应用于AUV，首先将式（10.26）压缩为式（10.30）的形式，

其中，f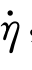（，η，t）包含非线性动力，包括科氏力和向心力、线性和非线性阻尼力、重力和浮力及力矩，以及外部干扰。

如果滑动表面定义为式（10.31），

当c为正时，可以看出，根据式（10.32），通过将s设为零并求解η导致η收敛到零。

无论初始条件如何。因此，控制问题简化为找到一个控制准则，使得式（10.33）成立。

这可以通过应用式（10.34）形式的控制准则来实现，

其中T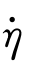（，η）足够大。因此，可以看出，应用式（10.34）将导致η收敛到零。

如果η现在被航行器的当前状态和期望状态之间的差代替，则可以观察到，应用这种形式的控制准则将考虑到要跟踪的参考轨迹。

SMC的两个变体包括了解耦SMC和耦合SMC。

（1）解耦SMC。

在AUV的动力学方程式（10.18）中，通过简化可以减少包含在各种矩阵中的系数数量。可以进行简化是由于航行器本体中存在的对称性、重心和浮力的位置，以及基于特定系数对航行器整体动力学的影响程度的假设。因此，假设体对称可以降低各种自由度之间的耦合水平。解耦SMC假设各个自由度之间不存在耦合，并且采用简单的操纵，使得其不激励这些耦合动力学。这对式（10.18）的影响是去除各种矩阵内的所有非对角线元素，这大大地简化了航行器的数学模型结构，并因此使得控制器的实现实质上更加容易。

（2）耦合SMC。

虽然去除了非对角元素降低了解耦SMC的计算复杂度，但它也对AUV的控制性能造成了一定的限制，特别是那些在高动态环境中运行并且需要执行复杂机动的AUV。考虑到这两个因素，这些非对角耦合项将对航行器的整体动力学产生影响，因此在控制准则的设计阶段不能被忽略。

耦合SMC是一种新颖的控制准则，与解耦SMC相比，它保留了式（10.18）中更多的耦合系数。此外，即使以这种方式设计控制器是非常规的，也选择体坐标系作为该控制器的坐标系。这种选择避免了式（10.26）和式（10.27）中将航行器模型从体坐标系转变到NED坐标系，尽管它确实需要将导航和航行数据从NED坐标系变换到体坐标系。通过式（10.35）定义NED坐标系中的位置和方位误差，

其中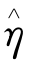表示由航行系统提供的当前位置和方位的估计，ηd表示由导航系统提供的期望位置和方位，需要单个转换来将该误差从NED坐标系转换到载体坐标系。

通常，期望的和当前的速度和加速度数据已经在载体坐标系中表示，因此，为了在载体坐标系中实现控制器，这里不需要进一步的转换。

如式（10.27）中所示，通过对比航行器模型转换成NED坐标系的解耦控制方案和将导航和航行数据转换成载体坐标系的耦合控制方案所需的转换次数，可以看出耦合控制方案涉及的转换较少，因此计算要求较低。