智能无人艇运动规划-海洋智能无人系统技术

USV的路径规划的目的是生成引导轨迹，通过遵循该轨迹进行航行，船舶能够自主地完成任务。在计算路径过程中，需要考虑各种实际条件，以确保生成的路径最优。通常考虑的成本包括距离最短、能耗最小、航行安全最大化等。

比较常见的运动规划算法可以大致分为两类，即确定性和启发式方法。确定性搜索方法通过遵循一组定义好的步骤来完成任务，具有完整性和一致性的特点。只要任务下达，就一定能够获得搜索结果；此外，在环境不变的情况下，输出的结果也会保持不变。然而，确定性搜索的主要问题之一是复杂空间条件下的运算时间过长。比较流行的确定性方法包括人工势场法、地图法、快FMM等优化算法。

提出启发式算法的初衷是为了解决一些确定性方法无法解决的特殊问题，并在难以找到精确的解决方案时提供近似解决方案。然而，因为启发式算法只搜索全局空间的子空间，因此不能保证结果的全局最优性，即只能获得接近最优的结果。此外，由于算法在空间中是随机搜索的，导致结果的一致性不如确定性方法。最典型的启发式算法为进化算法（evolutionary algorithm，EA），其中包括遗传算法（genetic algorithm，GA）、粒子群算法（particle swarm optimisation，PSO）和蚁群算法（ant colony optimisation，ACO）。

1）FMM算法

FMM最初是由J.Sethian于1996年提出的，用于迭代求解Eikonal方程以模拟物体的移动。Eikonal方程的形式为

|T（x）|V（x）=1

其中T（x）是点x到达物体处的时间，V（x）则是物体移动速度，Eikonal方程属于偏微分方程（PDE），当使用FMM时，可以使用积分的方法获得其数字解。FMM的求解过程类似于Dijkstra的方法，但以连续的方式求解。假设（x，y）是T（x，y）需要求解的点。则与之相邻的点则是一个包含四个元素的（x+Δx，y）、（x-Δx，y）、（x，y+Δy）、（x，y-Δy）的点集合，T（x，y）可以由以下式子获得

其中Δx和Δy则分别是x和y方向上的网格间距。

以上几个公式的解为

为了进一步说明FMM算法，图6.8展示了一个如何针对6×6网格图进行规划的简单案例。图6.8a显示了算法的初始配置，中间点是算法起点。网格尺寸为1×1，并且在每个点处将物体移动速度设置为1。FMM算法执行时，网格点被分为三个不同的组，如下所示：

远点（标记为浅蓝色）：包含具有未定到达时间值（T）的网格点。在运行FMM的第一步时，除起点之外的所有网格点都属于远点。

已知点（标记为红色）：包含具有确定到达时间值（T）的网格点。执行算法时，这类值不会被改变。

试验点（标记为绿色）：包含需要计算到达时间值（T）的网格点；但是，算法执行过程中这些值是可变的。

图6.8b展示了FMM执行的第一步，起点是目前唯一的已知点，T值为0。起点的四个相邻点由试验点组成，因此标记为绿色，计算的到达时间T为1。

对于下一步，将首先从试验集中选择具有最小到达时间成本的点作为新的已知点；如果四个相邻点的开销相同，则默认下方的点为最低开销点，此时该点被设定为已知点，而其相邻点则被设为试验点（如图6.8c所示）。步骤3和4则重复该过程来更新路线图，如图6.8d和e所示，最终的结果如图6.8f所示。在图6.8f中，观察到起点具有最小到达时间0；而其他点的到达时间与到起点的距离成正比增加，形成潜在场，其中势场值代表到达时间，最小势场值位于起点。

图6.8　使用FMM的更新过程

2）基于FMM的路径规划算法

表6.3中描述了基于FMM的路径规划算法，假设算法执行的路径规划空间如图6.9a所示，该空间有对应的二进制网格化地图，该算法首先读入M并计算其速度矩阵（V）。FMM基于V矩阵从起点计算到达时间矩阵T。生成的T（如图6.9b所示）可以被视为到达时间势场，其中势场值表示物体的到达时间，如果使用恒定速度矩阵，则势场值表示物体的到达距离。然后，基于到达时间矩阵T，通过应用梯度下降方法（如图6.9c中的红线所示）最终搜索最佳路径。然后，基于到达时间矩阵T，通过应用梯度下降方法（如图6.9c中的红线所示）搜索最佳路径。(www.xing528.com)

表6.3　FMM路径规划算法

另一种基于FMM的路径规划算法是Goez等人提出的平方律快速匹配（fast marching square，FMS）方法。与FMM相比，FMS生成的轨迹安全性更高，原因是该算法使船舶距离障碍物更远。FMS的表示方法见表6.4。它首先使用FMM将所有障碍物内的点展开一定范围以生成潜在安全区域。基于这个安全区域，从起点再次执行FMM以生成最终路径。使用与此前相同的地图，FMS生成的路径如图6.9c中的绿色线所示，该路径相比此前增加了安全性。

表6.4　FMS路径规划算法

最后，基于USV和FMS算法的运动学规则，Liu和Bucknall提出了角度引导快速行进算法（angle-guidance fast marching square，AFMS），目的是生成符合船舶动力学的轨迹（见表6.5显示的伪码）。它使用FMS作为基本算法，并且生成了符合USV的运动特性的轨迹，AFMS的核心是在规划空间（M）上创建“引导范围”（GR）（见表6.5中的第一行所示）。GR的形状如图6.10所示。它由两个不同的扇区组成，即白色部分的转弯范围扇区和阴影部分的障碍区域扇区。转弯范围扇区的尺寸由以下三个参数控制：

（1）距离（d）：锥形的半径，它能够控制影响路径的影响范围，并且与USV的波动运动速度有关。其中dmin是预定义的USV低速行驶情况下的最小安全距离［根据国际海事组织（International Maritime Organization，IMO）的推荐大约为船身长度的3到4倍］。范围量是用于调节GR范围大小的参数，以防止算法生成超大的障碍区域进而屏蔽终点位置。

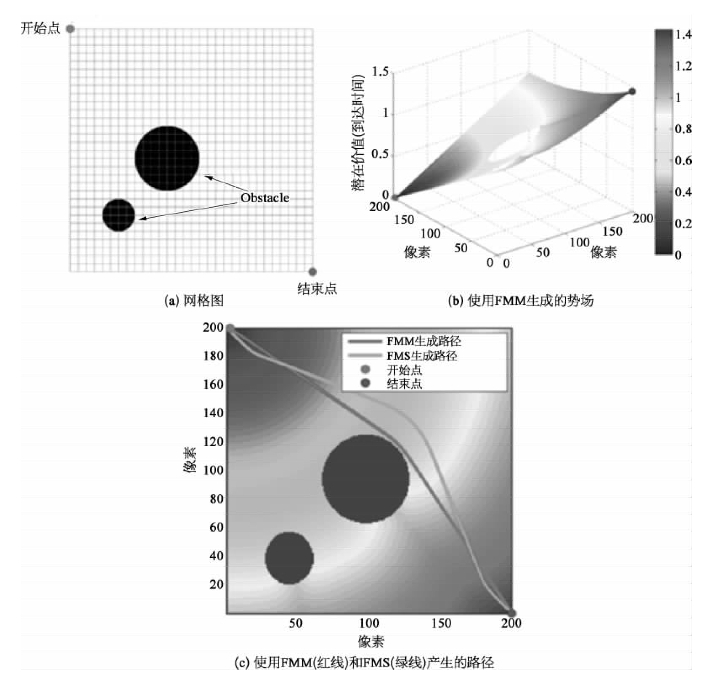
图6.9　路径规划算法示意图

每个点的势场值表示到起点的距离，势场值越高，到起点的距离越长

表6.5　AFMS

（2）航向角（α）：代表USV的当前航向并确定GR的方向。

（3）转向角（θ）：根据USV的偏航角极限计算得出的其中ΔT是时间步长而rmax则是偏航角变化率的上限。

θ=rmaxΔT

图6.10　GR图例

转弯范围扇区内的变化权值应该同规划空间M中的权值相同，另外，由于移动路径应包含于偏航扇区内，因此令障碍扇区的地位同障碍物一样，障碍扇区的网格势场值被指定为0。图6.10为GR图例。