如何处理模型的不确定性|海洋智能无人系统技术

参照USV的Springer导航系统中区间卡尔曼滤波技术的应用。在Springer导航系统中为卡尔曼滤波器和区间卡尔曼滤波算法的应用提供框架的是转向动力学的状态空间模型，用于估计船舶不确定建模假设的航向角。通过模拟揭示了区间卡尔曼滤波的几个特征，然后对其进行了讨论。图5.1所示为Springer双体船。

图5.1　Springer双体船

相较于配备有高规格导航设备（如无线电信标、雷达、陀螺罗盘）的大型商用船舶和战舰不同，USV相对采用的都是低成本的导航设备。

Springer的航向动力学模型（如图5.2所示）采用的是二阶状态空间模型，推进系统基于两台电机，分别位于船体的左右，当两台电机转速相同时，USV直线前进。定义两台电机的转速分别为n1和n2，那么定义有

图5.2　Springer运动动态模型

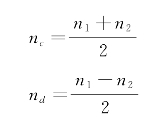
当nc恒定而nd变化时可以控制船体的转向，普利茅斯大学的研究人员在德文郡的罗德福德水库进行了实验，保持nc为900 r／min，记录了不同差值时船前进的角度以及系统所提供的推力，利用系统识别技术（system identification，SI）验证了航向动力学模型，在进行区间卡尔曼滤波时，需要GPS、数字罗盘、速度和深度四种传感器件通过串口连接至船上的计算机。

卡尔曼滤波器在航天领域已经应用得较为广泛，该算法的固有结构允许它自然地组合来自各种传感器的测量结果，权衡它们各自的精度。这促使卡尔曼滤波器作为融合来自低成本传感器数据的工具，以获得协同高度可靠的估计结果，这样较低成本的USV可以取代更精确的高价传感器。在航天器姿态估计中，卡尔曼滤波器是为了航天器携带的高精度惯性传感器而开发的，多传感器数据融合在陆地和海洋中的载具导航有着广泛的应用。这些载具通常会采用低成本INS与GPS定位数据进行集成。例如，弗吉尼亚理工大学开发的USV（VaCAS，2011）使用差分GPS、Micro Strain公司提供的基于微型机电系统（micro electro mechanical system，MEMS）广泛用于移动机器人应用程序的惯性传感器。

基本的卡尔曼滤波器方案对具有白高斯系统的线性系统和具有已知协方差的测量噪声可以进行统计上的最优估计，但其必须满足确定性矩阵可以被准确描述、初始状态及协方差可以被可靠估计这两个条件。以Springer为例，航向动力学模型用于卡尔曼滤波的预测阶段，其校正阶段使用航向角传感器指南针的数据进行校正，因为各个传感器获得的数据频率远高于USV运动状态更新速率，可以把航向数据视为瞬时数据。假设系统状态受随机输入干扰的影响，这一干扰为遵循确定协方差矩阵的均值为0的高斯白噪声序列，并且罗盘读数提供准确但不精确的测量同样遵循高斯白噪声分布，其平均值等于真实航向，以°（度）为单位，标准偏差为2°。(www.xing528.com)

标准的卡尔曼滤波依赖于已知的统计模型来描述不确定性。但是，如前所述，这些先验统计数据可能无法准确知晓，也可能随时间而变化。例如，GPS精度受到卫星位置、无线电信号干扰、山脉等信号的物理屏障或大气条件造成的影响，指南针读数可能受到干扰电磁场的影响。在这种情况下，必须不断调整测量噪声协方差R以适应传感器精度的变化，以便从卡尔曼滤波获得良好的性能。同样，理想情况下可以在变化的系统噪声协方差Q中考虑变化的海平面粗糙度和影响系统的其他随机效应，其最准确地反映每个时刻的条件。卡尔曼滤波还假设矩阵描述的确定性动力学是精确建模的；然而，改变有效载荷，平均风速或当前力等将转化为缓慢变化的动态，这将需要模型不断更新。虽然有许多技术试图通过引入自适应机制来提高卡尔曼滤波的可靠性，但这些技术通常不能保证所有情况下估计的结果变好，或无法提供严格的误差范围。

区间分析在20世纪50年代开始正式研究，目的是找到一种方法来限制有限精度数值计算中的舍入误差。由于计算机表示受机器二进制的限制，在计算机上只能准确表示一小部分实数，但每个实数可以通过适当的四舍五入，由计算机进行二进制表示，也因此有了区间运算（interval arithmetic，IA）的定义，如果已知误差的初始界限，那么以有限精度执行的任何计算中固有的误差传播将自动受到使用IA计算过程的限制。

在20世纪90年代，卡尔曼滤波开始应用于动态区间系统的分析，通常这样描述系统建模中的不确定性，即物理参数通常不是精确已知的，具有一定的公差，或具有不同的性质。例如，如前所述，除了其他参数，海面上航行的船的动力学模型取决于其质量，其质量取决于乘客数量。在USV模型中也是一样的，随着任务的不同，USV的载荷也会出现区别。在Springer状航向动力学模型中，使用SI技术，在特定试验期间采集的特定数据集来获得矩阵的系数。在其他试验期间，由于诸如先前概述的原因，所获得的值可能略有不同。但是，如果执行整个范围的实验，则可以间隔性地包括变化的结果，从而产生包含所获得的每个单独模型的区间系统模型。通过这种方式，所有可能的动态都被考虑在内。

从相同的原理推导出来，区间卡尔曼滤波在统计上与标准卡尔曼滤波在相同的意义上是最优的，并且保持了相同的递归公式。然而，与点估计相比，计算的区间估计的主要优点是，它们保证包含区间模型中包含的单个模型的所有卡尔曼滤波估计，这是由于IA的包含性，如果包含初始不精确数据在严格的边界内，用这些边界进行计算，得到实际解范围的严格边界。图5.3为区间卡尔曼滤波估算误差的变化。

基于相同的原理，区间卡尔曼滤波与标准卡尔曼滤波具有相同的统计最优性，并保持了相同的递推公式。然而，通过利用计算区间估计取代点估计的方式，保证了包含所有个人的卡尔曼滤波估计模型都处于区间模型中，这样的好处是，如果最初的不精确的数据都被封闭在严格的范围内，实际求解出来的也是一个包含着严格边界的解。

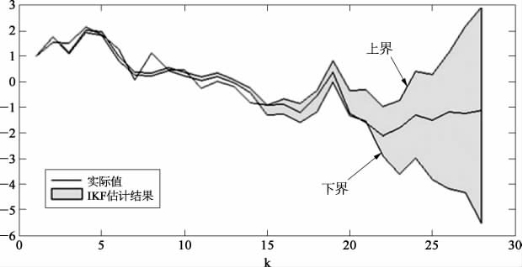
图5.3　区间卡尔曼滤波估算误差的变化

USV的状态估计要求较为精确地进行评估。如果已知真实的系统动力学包含在区间模型中，那么使用区间卡尔曼滤波可以进行一个状态估计。虽然不知道这个估计值的精确值，但是对于所需的目的，已给小范围的给定区间是可以接受的。例如，如果对象要在两个极限值之间保持一个状态变量，只要区间估计值保持在这些极限值之内，就不需要控制操作。同样，如果评估边界渗透到不希望的操作区域，则可以使用它来发出警报或触发其他应急机制。

虽然大多数USV通常是远程操作，但对自动化水平不断提高的USV的需求正在增加。随着大量新兴的USV平台以及卡尔曼滤波在导航和传感器融合中的广泛应用，目前正在开发研究用于USV的强大导航技术，这就对状态估计提出了更高的要求，因为实际应用中海洋条件、有效载荷等船舶特征会产生变化，这些变化转化为动力学模型中的不确定性，通常很容易受到区间的限制。对于区间系统模型，区间卡尔曼滤波是卡尔曼滤波的自然延伸，在面对这种有界模型不确定性时，它为估计提供了严格的界限，为实际处理模型的不确定性提供了巨大的帮助。