本节介绍的算法用来将两个容器或区间的元素合并、交集和差集。其中合并运算主要包括总和、并集、交集等。
1.两个有序集合的总和
merge()算法可用来处理两个有序集合的总和。其原型为:

上述两种形式均是将两个区间[first1,last1]和[first2,last2]内的元素合并,并将合并后的所有元素保存在以x为起始的目标区间内。目标区间内的所有元素都将按顺序排列。其返回值为目标区间的最后一个被复制元素的下一位置。二元判断式comp是可有可无的,用户可以自定义二元判断式以作为序列的排序准则。merge()算法对两个源区间没任何变化。
源区间(源容器)中的元素应该是有序的。在多数情况下,merge()算法可以将两个无序的容器(源区间)合并到一个无序的目标区间中。通常,使用copy()函数会更方便些。在使用merge()算法时,要保证目标区间足够大,否则需要使用插入型迭代器。
一般情况下,目标区间和源区间不允许重复。但是,merge()算法没有保证新生成的区间(容器)中元素的唯一性。
list型容器提供了一个特殊成员函数merge(),用于合并两个list型容器中的元素。
2.两个已排序集合的并集
set_union()算法用于实现将有序的两个区间内的元素合并,获得以指定起始位置开始的目标区间。新生成区间内的元素来自于两个源区间,但是重复的元素被唯一化。其原型为:

其中[_First1,_Last1]和[_First2,_Last2]表示两个源区间,参数_Result代表新生成的目标区间的起始位置。
当源区间内已经含有重复的元素时,使用set_union()算法会保留这些重复的元素。此时元素的重复个数是两个源区间中内的重复个数较大的那个数值。
_Comp是一个二元判断式,可作为排序准则。
3.两个有序集合的交集
set_intersection()算法用于实现将有序的两个区间的元素合并。新生成区间内的元素应该是那些同时属于两个源区间(容器)的元素。如果两个源区间内原来存在重复元素,新生成的目标区间内也包含重复元素,重复个数为两个源区间中较小的那个重复个数。其原型为:

其返回值是输出型迭代器,迭代器指向目标区间的最后一个被“合并”元素的下一个位置。目标区间内的所有元素均按顺序排列。
4.两个有序集合的差集(https://www.xing528.com)
set_difference()算法实现将实现两个源区间之间的差集,新生成区间内的元素是仅只包含在第一个源区间中的元素。其原型为:

第一个源区间中所有存在于第二个源区间中的元素将不存在于新生成区间中。和前面的合并算法一样,新生成区间内的元素均是有序的。
若源区间内有重复元素,则目标区间内相应的也会包含重复元素。重复元素的个数是第一源区间内的重复个数减去第二源区间内的相应重复个数;若第二个源区间内的重复个数大于第一源区间内的相应重复个数,则目标区间内的对应重复个数将等于0。
算法对源区间不做任何修改,并且两个源区间都是有序的。目标区间和源区间不允许重叠。
另外,STL中还存在另一种算法set_symmetric_difference()。该算法可以实现两个源区间的合并,并生成新区间。新生成区间中不包含两个源区间中共同存在的元素。和前面的合并算法一样,新生成的目标区间的元素均是有序的。其原型为:

5.连贯的有序区间的合并
inplace_merge()算法可以将两个有序区间[beg1,end1beg2]和[end1beg2,end2]的元素合并,使区间[beg1,beg2]成为两者之和。其原型为:

下面以例4-30来阐释上述几种算法的使用方法。
例4-30
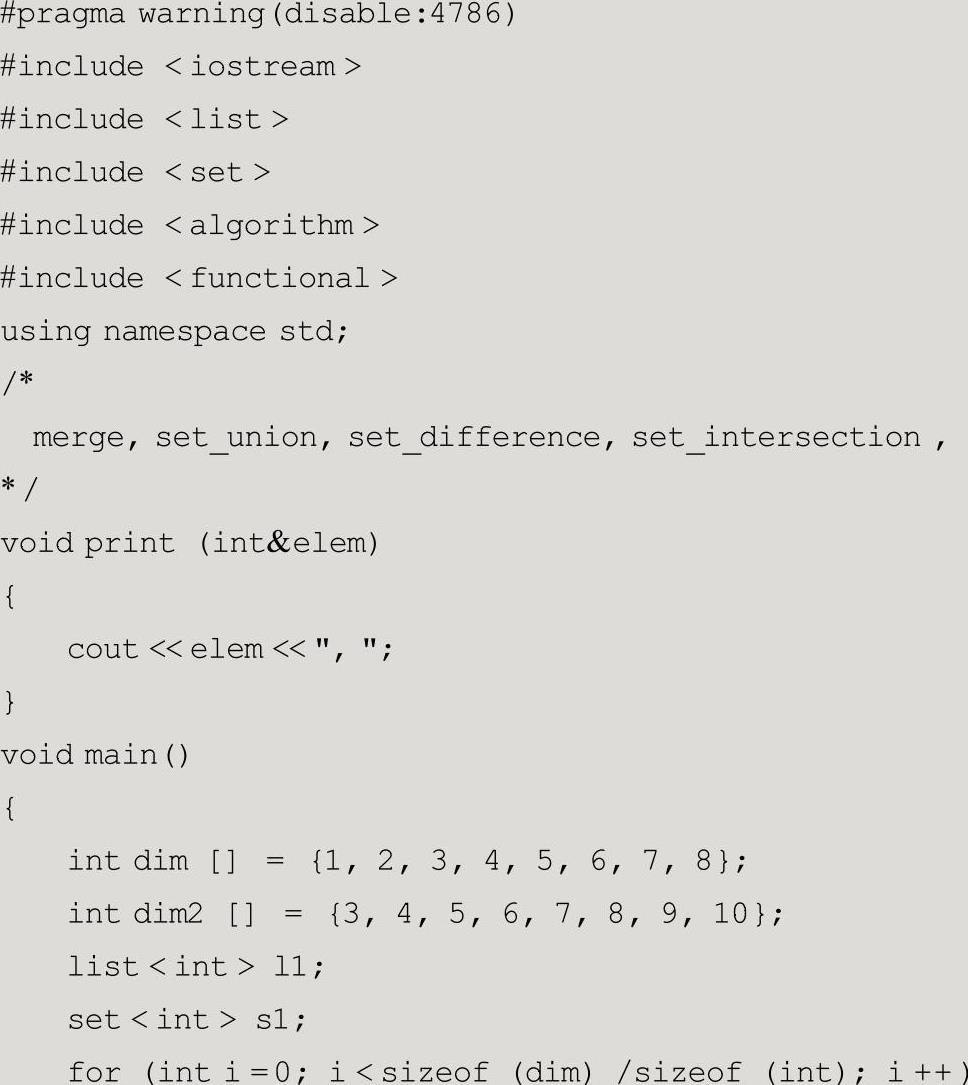

例4-30的执行效果如图4-30所示。

图4-30 例4-30的执行效果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




