自动反馈控制器在软件工程专业导论中的应用

将上述图8-1抽象成如图8-2所示的闭环自动控制框图。控制器解释为离心调速器,被控系统是蒸汽推动的大转轮。大轮的转速和离心器的转速具有相关性,这样离心器就能把当前的转速转换为需要的蒸汽量——即传感器。

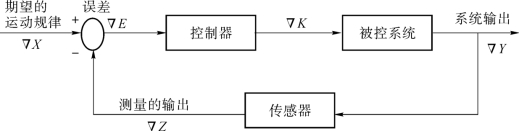
图8-2 抽象的闭环控制系统

一般被控系统具有自己特定的动力学特征,例如,机械运动符合牛顿第二定律F=Ma,M是质量,a是加速度,a的一次积分是速度V,再次积分是运动距离。

这样,我们假设,设计一个控制器,这个控制器发出推力F,将一个物体从一个地方Y(0)直线地推到另一个地方Y(T),那么,输入X=Y(T)-Y(0)。

推动力K 是控制器发出来的。K 与物体当前位置Y(t)和期望位置Y(T)相关联的函数,即K=f(E(t)),最简单的形式是K=k×E(t),而E(t)=X-Z(t),即简单的比例关系。而Z(t)=S(Y(t)),S 表达传感器的传递函数。

现在,求K 为多少?能使得在最短的时间内,让物体从Y(0)的位置,移动X 距离到Y(T),使得T 为最小的K?K 是一个函数。

由于物体(被控系统)是有惯性的,当物体接近终点时,如果K 始终是一个常数,那么,就会将物体推过期望的位置,需要用-F(反向)的力再推回来,如果不考虑地面的摩擦系数,可能会永远推不到期望的位置,即围绕终点位置的震荡,而不能达到期望的终点,甚至离目标越来越远。

K 是一个函数,而不是一个常量。K 不仅与物体的位置相关,也与速度(位置的导数)和加速度(速度的导数)相关。(www.xing528.com)

进一步假设,被推动的物体在一个多维空间里,如何求得K?

在空间里,上面的变量成为一个向量,表达为∇X、∇K、∇Y、∇Z,分别代表控制器的输出,被控系统的输出、传感器的输出。它们被解释是一组向量,向量是一组变量的集合,例如,X 的值、X 的一阶导数(速度)、X 的二阶导数(加速度)以及多阶导数等。

例如,一部电梯,不仅要用位置表示其运动状态,还要用速度和加速度表示其状态,如果加速度太快,乘客是受不了的。电梯控制器K 不仅仅控制电梯的开启和停止位、还包含运动的速度(不能太快或太慢),加速度不能过大。

∇X、∇K、∇Y、∇Z 之间的关系可以用一组微分方程描述。如果已知∇X、∇Y、∇Z,求∇K 就是设计控制器。因此,系统控制设计师必须:

(1)搞清楚被控对象的动力学方程,通常要用一组微分方程表达;

(2)知道传感器的动力学方程,也可能是一组微分方程;

(3)控制器也是一组微分方程,其输入向量是∇E,输出向量∇K,用来控制被控对象,使得∇Y 按期望的运动规律运动。