软件工程专业导论：链表的介绍及其在计算机内存中的应用

二维或多维数组都可以看成是一维数组,只要按严格的顺序排列,例如,把二维数组的第二行接到第一行的后面等。就成为按行排的一维数组。当然,也可以按列排。因此,多维数组在内存中的存放与一维数组是一样连续存放的,如图2-8所示。

如果删除数组中一行或一列或一个元素,或在某个元素前插入一个元素的话,所花费的时间太长,因为,必须移动后面的元素。

对此,人们发明了链表。链表由若干个在计算机内存中不连续存放的数据结点组成。数据结点有两部分组成:一个数据区和一个指针(即内存地址编号),如图3-3(a)所示。结点中的数据区可以放一个基本数据类型的数据(参见3.4节),也可是一个结构体类型的数据(参见3.6.2节)。结点中指针代表了它所指向的下一个结点,这样多个结点连起来就是一个链表,如图3-3(b)所示。最后一个结点的指针为“空”(记为:∧),请思考一下如何表达“空”?

如果要删除一个结点,仅仅需要修改前后结点的指针,如图3-3(c)所示。

要如果要在两个结点之间插入一个结点的话,仅需要更改相关联的结点的指针即可,如图3-3(d)所示,而不用大量的移动结点。(www.xing528.com)

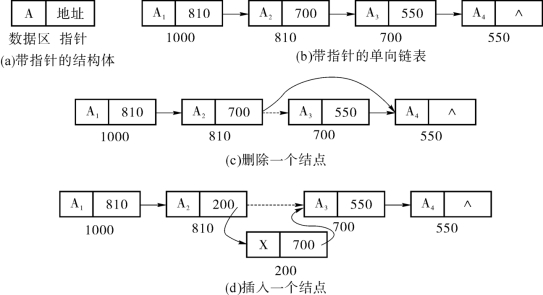
图3-3 链表操作

使用单向链表,正向寻找一个结点非常方便,但是要反向寻找一个结点,就困难了,对此,可以创立双向链表。如果把链表的最后一个单元的指针指向第一个结点,就形成了循环链表。

把许多结点按一定的排序重新排列是经常的运算,用链表进行排序比用数组要方便得多。