运算问题解决方案-软件工程专业导论

浮点运算中会出现三类问题:第一类问题是舍入(round);第二类是非数问题;第三类是正负无穷大(小)的判断问题。

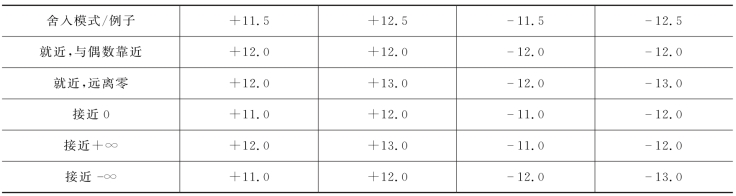
第一类是舍入问题,IEEE-754给出了5个原则,具体举例如表3-4所示。

表3-4 浮点数的舍取原则

第二类是非数(Na N)问题。非数(NaN)包括例子3、例子4和例子5的三种情况。Na N在运算时会发生如下三种情况。

(1)正常的数x与一个Na N 数进行运算,例如与Na N 做比较运算,情况如表3-5所示。

表3-5 正常数与NaN 数做比较

即正常数与NaN 做比较的结果,总是不相等的。

(2)运算不定情况,分为

·除法:(±0)/(±0)和(±∞)/(±∞)。

·乘法:(±0)×(±∞)和(±∞)×(±0)。

·加法:(+∞)+(-∞),(-∞)+(+∞)。(www.xing528.com)

·减法:(+∞)-(+∞)和(-∞)-(-∞)。

·幂运算:标准的pow 函数,指数部分是整型的,例如,00、1∞、和∞0 应当为1。

(3)运算时,结果产生复数的情况,例如

·负数求平方根;

·负数的log;

·sin(x)或cos(x)求逆时,其中的x 小于-1或大于1。

第三类是正负无穷大(小)的判断问题。

为了保证浮点运算的安全性,需要判断浮点处于危险境地——一个Na N(参见例子3和例子4)并不代表这个数不是数,只是说明如果用该数与正常数进行运算,很容易发生问题(例如,上溢出和下溢出——超出数的表达范围)。IEEE-754标准把Na N 区分为qNaN-(quite NaN)和sNaN(signaling NaN)。

IEEE-754标准中用小数部分的最高位进行区分,如果是1,则该数是q NaN,否则是s NaN。

q NaN:不会立刻引起计算机异常,是为了计算留出余量。但又不能忽略,否则输出的数据没有意义。因此,在运算时要判断出qNa N 的发生,就不能再进行计算了。如果仍坚持做计算,就可能发生上溢出或除零错,导致计算机死机。

s Na N:意味着,更不安全(余量更小了)。这是NaN 的特殊形态,即使对qNaN 情况都做了处理,也会出现sNa N 的情况。例如,用s Na N 数填充了一块未初始化的内存,恰好把某个变量分配给了这个内存,如果用这个变量进行计算,自然会产生非法的运算。

可以把s NaN 作为更复杂数据项的符号,用于表达:①具有下溢出的数;具有上溢出的数;②企图表达的更高精度的数;③复数情况。这样,在运算时,可以判断各种情况,并给出相应的处理,如直接给出非数参与运算时的结果。