【摘要】：2012年诺贝尔物理学奖授予法国科学家塞尔日·阿罗什与美国科学家大卫·维因兰德,以表彰他们在量子物理学方面的卓越研究。塞尔日·阿罗什采取了相反的方法:通过发射原子穿过阱,控制并测量了捕获的光子或粒子。图2-14 量子的状态与量子位图2-14中,量子位可以用粒子的旋转状态:自旋加快(向上)和自旋减慢(向下)表达,记为:|↓〉和|↑〉,或|0〉和|1〉。
2012年诺贝尔物理学奖授予法国科学家塞尔日·阿罗什(Serge Haroche)与美国科学家大卫·维因兰德(David Wineland),以表彰他们在量子物理学方面的卓越研究。这两位物理学家用突破性的实验方法使单个粒子动态系统可被测量和操作[5]。
大卫·维因兰德是利用光或光子来捕捉、控制以及测量带电原子或者离子。塞尔日·阿罗什采取了相反的方法:通过发射原子穿过阱,控制并测量了捕获的光子或粒子。
既然,微观粒子是可测量和可控制的,那么,就可能用粒子的状态集合表达数的集合,控制从某个状态迁移到另一状态,就可能实现图灵机提出的状态表的迁移,如表2-2所示,或冯·诺依曼机的二进制的状态,或替代集成电路中的逻辑门。
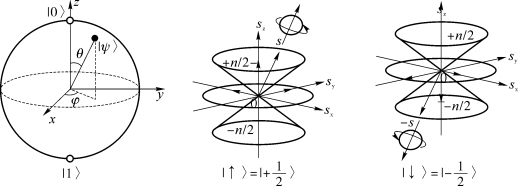
一个粒子在空间的运动,可以用布洛赫球面(Bloch sphere)表达,如图2-14所示。顶点和底点(北极和南极)典型的分别对应于标准基本向量|0〉和|1〉,即电子的自旋加快和自旋减慢。
(www.xing528.com)
图2-14 量子的状态与量子位
图2-14中,量子位(qubit)可以用粒子的旋转状态:自旋加快(向上)和自旋减慢(向下)表达,记为:|↓〉和|↑〉,或|0〉和|1〉。这类表现为静自旋的例子有:质子、中子、电子、中微子和夸克。那么,就可以寻找容易能测量和控制粒子的材料,从而用可控的粒子状态实现计算。
注意:量子运动是一个球面,而不是一个平面(PN 结的状态是平面,两个状态)。球面的状态要用空间复数表达(可以选修《复变函数》)。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
