巴贝奇机器：实现更复杂计算

1.4节只讨论了用巴贝奇机器计算加减法,这是不够的! 能否让机器做更复杂的计算呢?考虑如下的二次多项式:

如果直接计算,就需要做乘法计算。乘法计算是一个难题。能否消除乘法计算呢?巴贝奇提出用差分进行计算的方法,解决多项式的计算,并把自己制造的机器称为差分机(difference engine)。

可以先算出值p(0)、p(1)、p(2)、p(3),p(4)等。构造出如表2-1所示的差分计算方法。

表2-1 一个二次多项式的差分表

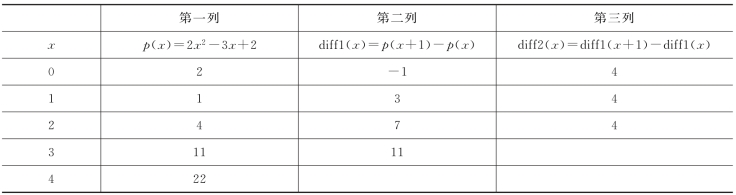
注意:第三列的值是常数。事实上,n次多项式的n+1列总是常数。因此,可以构造出n次多项式的差进行计算。

例如,计算p(3),则有

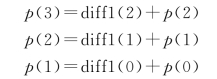
可以查表得到diff1(0)、diff1(1)和diff1(2)。或直接计算:

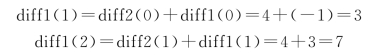
这样,一个多项式p(x)=2x 2-3x+2的计算就转换成利用差分方式的加减法计算,从而避免了麻烦的乘法运算。

更一般地,对于任意的多项式

(www.xing528.com)

可以造出类似于表2-1的各列的值如下:

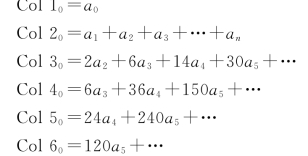
Ada与可编程计算

这样,f(0)就是Col 10=a0;Col 20是f(1)和f(0)的差。

由于各种复杂的函数(如三角函数、对数等)都可以用麦克劳林或泰勒级数表达,因此,可以用巴贝奇的差分机器计算出所有复杂的函数值。

艾达·洛芙莱斯(Ada Lovelace)进一步描述了如何用巴贝奇差分机计算伯努利数(Bernoulli numbers)^[1]的计算步骤,如图2-1所示(注:该图是原图的照片,读者不必在乎是否清晰,要关心注释所给出的方法、步骤、中间结果的存放)。

图2-1中不仅给出了计算步骤和计算符号(加、减、乘),还给出接收结果的变量、变量值可能的变化、每个步骤的计算公式,以及初始数据区、存放中间结果的变量区和最终结果变量区。

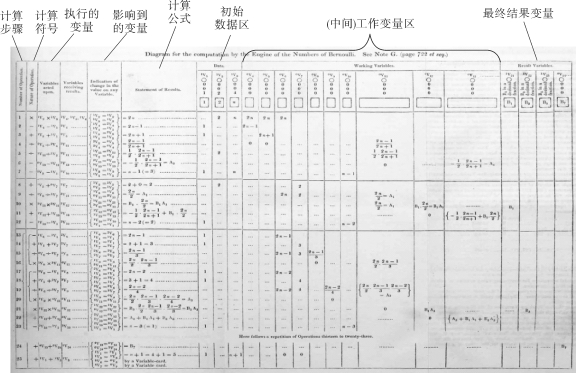
图2-1 在巴贝奇差分机上计算伯努利数的算法步骤

事实上,Ada提出的算法是一个计算步骤,如果差分机能按这个步骤一步步地计算,就能得到最后的结果。Ada认为,巴贝奇的机器和以前计算机器的根本差别在于:能够事先编写一系列的计算步骤,实现复杂的计算。这一系列的计算步骤就是计算机器自动执行的程序。

虽然,可编程设备可以追溯到1206年,用凸轮等装置实现有节奏地敲击音乐,以及1801年,雅克布(Jacquard Loom)通过系列的穿孔卡片实现纺织机织出不同花色的机器。然而,Ada是第一个描述用机器按步骤进行计算和变量存储实现自动计算的人,这为后来的可编程计算奠定了方法学基础。Ada的编程思想被后来者接受。1980年,美国国防部以Ada的名字命名了Ada编程语言。大家公认Ada是第一个程序员。