码制与单片机原理应用实例，包括补码和原码的计算方法

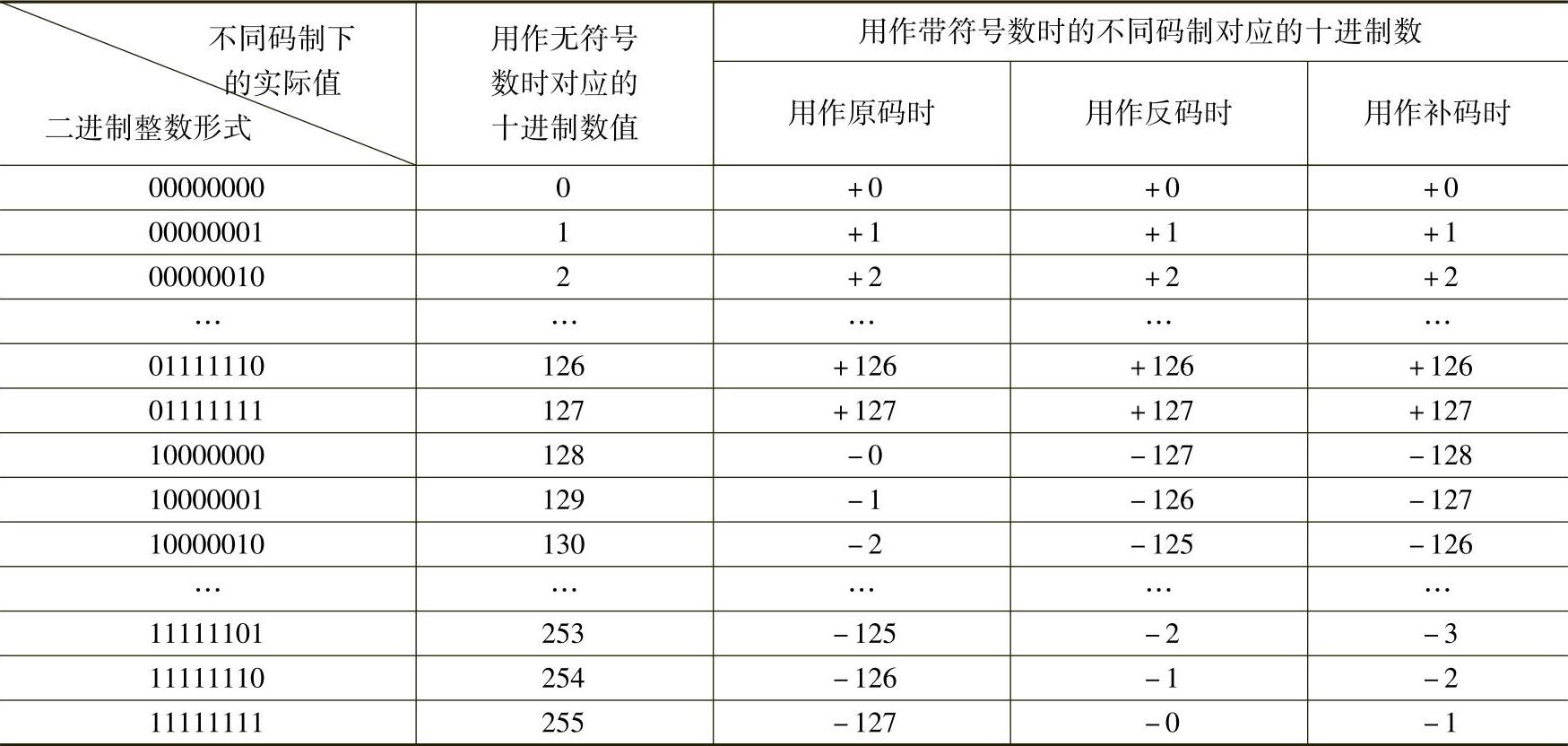
单片机中所处理数的基本形式是二进制数码，为运算方便起见，单片机采用的码制有原码、反码和补码三种形式。二进制数用作不同码制数时的实际值对照见表1-3。

表1-3 二进制数用作不同码制数时的实际值对照表

1.原码

原码是单片机中所处理数的原形，也就是用户按二进制数表示法输入单片机的数。原码可以是无符号数，也可以是有符号数。以单片机常用的8位二进制数为例：原码为无符号数时，8位二进制数00000000B～11111111B就和0～255的自然数一一对应。

原码为有符号数时，8位二进制数00000000B～11111111B就要按最高位的值分为正数与负数两种，即最高位为符号位，其余为数值位。如：

符号位为0时，数为正，+1010B的原码为00001010B；

符号位为1时，数为负，-1010B的原码为10001010B。

2.反码

反码在运算过程中使用。

1）正数的反码=原码。

2）负数的反码：符号位=原码的符号位，数值位=原码数值位按位取反，如-1010B的八位反码为：11110101B。

3.补码

补码是为了单片机简化减法运算，用加法完成减法的一种码制。

（1）补码的定义 正数的补码表达形式就是正数本身，有X_原=（X）补，负数的补码表达形式（X）补就是模减原码的绝对值，有（X）补=模-|X_原|。

这里，模与机器数的位数有关，如8位2进制数的模为2⁸=100H，当8位二进制数X=0FFH时，对X再加1，就会超出8位二进制数的表达范围，产生溢出或进位，即X+1=0FFH+01H=100H=进位+00H，这意味着当机器数从0开始增加到模的数值就会重新从0开始循环计数，模的具体值是超过机器数规定范围1的值，对8位二进制数，模就是2⁸=100H。

（2）补码的作用 补码是将单片机中的减法变为加法的数码。比如X-Y，这个Y，可以看作-Y，就变成X+（-Y），X和Y本身是原码，把Y变成补码表达形式-Y，就可以做加法。

举一个简单的例子：已知X₁=02H，X₂=01H，试求X₁-X₂的值。

由于计算机在累加器中只能进行加法，这样就必须采用补码的方式将原码的减法变为补码的加法，下面是其演变过程。(www.xing528.com)

X₁^-X2=X₁+（-X₂）=X₁+（模-|-X₂|）-模=（X₁）_补+（-X₂）_补-模

这里，X₁=02H，正数的补码表达形式就是其原码，即X₁=（X₁）补=02H；而-X₂是负数，其补码表达形式就是（模-|-X₂|），即（-X₂）补=100H-01H=0FFH。另外，从表1-3也可看出十进制数-1的补码表达形式是11111111B，即0FFH。

则，X₁-X₂=（X₁）_补+（-X₂）_补-模=02H+0FFH-100H=01H+100H-100H=01H

由这个例子可以看出，采用补码后，出现的-模是借位，由于大数减小数必然产生模的溢出，则可消去借位，而小数减大数就会借位。这样就通过补码引入借位，并利用超过模后产生溢出进位，重新从0计数的性质，使减法变成加法。

这里再强调一下，在表1-2中给出的是机器数在用作各种码制包括补码时的含义。如，01H在用作补码表达形式时的含义是01H，即+1D，或者说正数01H的补码表达形式仍是01H。而0FFH在补码表达形式时的含义是-1H，即-1D，或者说负数-01H的补码表达形式是0FFH。这是因为，根据补码定义，负数的补码=模-|原码|有：

（-01H）_补=100H-|-01H|=0FFH

4.补码的简便求法

上述按定义求模码的过程非常繁琐，在单片机实际操作时是采用反码+1的简便方法来求补码的。即：

补码=（原码）_反+1

如：-01H的反码表达形式为11111110B或0FEH，-01H的补码表达形式就是

（-01）_补=（-01）_反+1=0FEH+1=0FFH

这一求法的原理是：补码表达形式=模-|原码|=100-|原码|=（0FFH-|原码|）+1，而前述负数的反码表达形式为原码的绝对值按位取反，即0FFH-|原码|，所以补码表达形式=（原码）_反+1。

在单片机中采用补码表示有符号数时，可将减法变为加法，此时将减法变为加法的“取补”过程是由CPU自动进行的。用户使用补码时需注意三点：

1）输入的操作数必须是补码表式形式，其中正数的补码表式形式=原码，负数的补码表式形式=模-|原码|。

2）加/减计算结果仍为补码表达形式。

3）原码为负数时可以用其反码来简化求取补码表式形式的过程。

补码表达形式=模-|原码|=100H-|原码|=（0FFH-|原码|）+1=（|原码|）_反+1

即负数的补码为其绝对值取反再加1，如（-3）_补=（-3）_反+1=（10000011）_反+1=11111100B+1=11111101B=0FDH