数制转换方法，示例含十六进制，二进制转换法

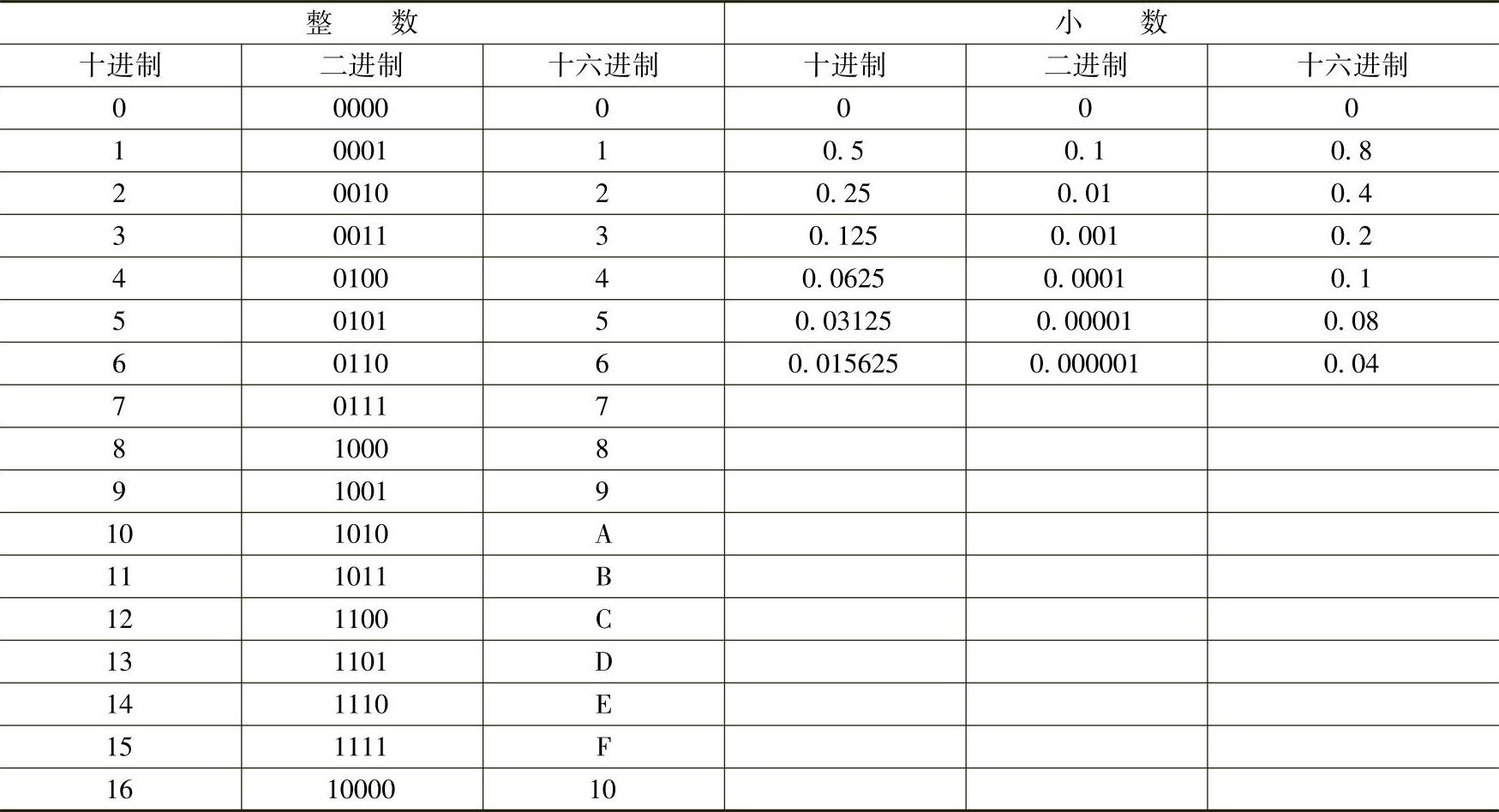
与各种微型计算机一样，单片机中常用的数制是二进制、十进制与十六进制三种，部分二进制、十进制与十六进制数对照见表1-2。十进制是我们最熟悉的进位计数制，其特点是逢十进位。本节主要讲二进制、十六进制的特点以及二进制与十六进制、十进制间的转换方法。

1.二进制

二进制的特点：数码为0、1；逢2进1，借1顶2。

二进制数以幂级数形式表示时，2为基数，其i位的权是2ⁱ。如：

101101.11B=1×2⁵+0×2⁴+1×2³+1×2²+0×2¹+1×2⁰+1×2^-1+1×2^-2=32+0+8+4+0+1+0.5+0.25=45.7

其中最高位的权是2⁵，次高位的权是2⁴……依此类推。

二进制数N的通式是各位的数码a_i与其所在位的权2ⁱ乘积之和。即

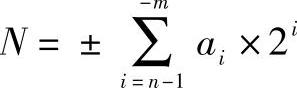
式中 n——整数部分位数；

m——小数部分位数；

a_i——第i位数码；

2ⁱ——第i位数的权。

表1-2 部分十进制、二进制和十六进制数对照表

2.十六进制

十六进制的特点如下：

1）16个数码为0、1、2、3、4、5、6、7、8、9、A、B、D、D、E、F，其中A、B、C、D、E、F相当于10、11、12、13、14、15。

2）逢十六进一，借一顶十六。

十六进制数以幂级数形式表达时，16为基数，其i位的权是16ⁱ。十六进制数的最后均标有字母H。如：FAH=F×16¹+A×16⁰=15×16+10×1=250。

十六进制数N的通式也是各位的数码a_i与其所在位的权16ⁱ乘积之和。即

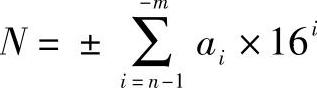
式中 n——整数部分位数；

m——小数部分位数；

a_i——第i位数码；

16ⁱ——第i位数的权。

十六进制数比起二进制数的优点是书写记忆方便，所以在微机编程等场合应用最广。(www.xing528.com)

3.二进制数与十六进制数转换

（1）二进制数转换成十六进制数 转换方法是4位合1位法。即，以小数点为界，向前、后每4位二进制数合1位十六进制数，不够4位补“0”，如：

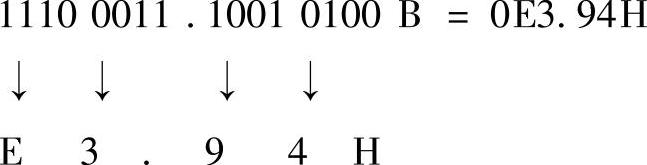
（2）十六进制数转换为二进制数 转换方法是每位转成4位法，以小数点为界每位十六进制数转换为4位二进制数，如将上例逆转一下，就有0E3.94H=11100011.10010100B

4.二进制数、十六进制数与十进制数转换

（1）二进制数、十六进制数转换成十进制数 转换方法是按权展开，然后按照十进制运算法则求和。例：

1011.1010B=1×2³+1×2¹+1×2⁰+1×2^-1+1×2^-3=11.625

DFC.8H=13×16²+15×16¹+12×16⁰+8×16^-1=3580.5

（2）十进制数转换成二进制数、十六进制数

1）整数转换法。“除基数取余法”：十进制整数不断除以转换进制基数，直至商为0。每除一次取一个余数，从低位排向高位。例：

十进制数转换成二进制数：

由此得到：53=110101B

十进制数转换成十六进制数：

208÷16=13余0

13÷16=0余13=DH

由此得到：208=D0H

2）小数转换法。“乘基数取整法”：用转换进制的基数乘以小数部分，直至小数为0或达到转换精度要求的位数。每乘一次取一次整数，从最高位排到最低位。例：

十进制数转换成二进制数：

由此得到：0.375=0.011B

十进制数转换成十六进制数：

0.625×16=10.0

由此得到：0.625=0.AH