A*算法又叫A-Star算法,在游戏中它有很典型的应用,是人工智能在游戏中的代表。A*算法在人工智能中是一种典型的启发式搜索算法,为了说清楚A*算法,请读者先了解下面几个概念。
(1)启发式搜索:启发式搜索就是在状态空间中对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
(2)评估函数:从当前节点移动到目标节点的预估费用;这个估计就是启发式的。在寻路问题和迷宫问题中,我们通常用曼哈顿(Manhattan)估价函数(下文有介绍)预估费用。
(3)A*算法与BFS:可以这样说,BFS是A*算法的一个特例。对于一个BFS算法,从当前节点扩展出来的每一个节点(如果没有被访问过的话)都要放进队列进行进一步扩展。也就是说BFS的估计函数h永远等于0,没有一点启发式的信息,可以认为BFS是较差的A*算法。
(4)选取最小估价:如果学过数据结构的话,应该可以知道,对于每次都要选取最小估价的节点,应该用到最小优先级队列(也叫最小二叉堆)。在C++的STL里有现成的数据结构priority_queue可以直接使用。
(5)A*算法的特点:A*算法在理论上是时间最优的,但是也有缺点:它的空间增长是指数级别的。
(6)IDA*算法:这种算法被称为迭代加深A*算法,可以有效地解决A*空间增长带来的问题,甚至可以不用到优先级队列。
1.启发式搜索算法基础
在讲解启发式搜索算法之前先简单介绍状态空间搜索。状态空间搜索,如果按专业的说法就是将问题求解过程表现为从初始状态到目标状态寻找这个路径的过程。通俗点说,就是在解一个问题时,找到一条可以从求解的开始到问题的结果的过程。由于求解问题的过程中有很多分支,主要是求解过程中求解条件的不确定性和不完备性造成的,这使得求解的路径很多。这就构成了一个图,通常将这个图称为状态空间。问题的求解实际上就是在这个图中找到一条路径可以从开始到结果。这个寻找的过程就是状态空间搜索。
前面说的广度和深度优先搜索有一个很大的缺陷:它们都是在一个给定的状态空间中穷举。这在状态空间不大的情况下是很合适的算法,可是当状态空间很大,且不预测的情况下就不可取了。效率实在太低,甚至不可完成。在这里就要用到启发式搜索了。
采用了不同的估价可以有不同的效果。我们先看看估价是如何表示的。
启发中的估价是用估价函数表示的,例如:

其中f(n)是节点n的估价函数,g(n)实在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。在这里h(n)体现了搜索的启发信息,因为g(n)是已知的。如果说详细点儿,g(n)代表了搜索的广度的优先趋势。但是当h(n)■g(n)时,可以省略g(n)而提高效率。
一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件如下。
(1)搜索树上存在着从起始点到终了点的最优路径。
(2)问题域是有限的。
(3)所有结点的子结点的搜索代价值>0。
(4)h(n)≤h*(n),其中h*(n)表示实际问题的代价值。
当上述4个条件都满足时,一个具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法,并一定能找到最优解。对于一个搜索问题,显然,条件(1)、(2)、(3)都是很容易满足的,而条件(4)则是需要精心设计的,因为h*(n)是无法知道的。所以,一个满足条件(4)的启发策略h(n)就难能可贵了。不过对于图的最优路径搜索和八数码问题,有些相关策略h(n)不仅很好理解,而且已经在理论上证明是满足条件(4)的,从而为这个算法的推广起到了决定性的作用。不过h(n)距离h*(n)的程度不能过大,否则h(n)就没有过强的区分能力,算法效率并不会很高。对一个好的h(n)的评价是:h(n)在h*(n)的下界之下,并且尽量接近h*(n)。
当然,评估函数的设计也就仅仅是f(n)=g(n)+h(n)一种,另外的评估函数“变种”,如:f(n)=w*g(n)+(1-w)*h(n),f(n)=g(n)+h(n)+h(n-1)针对不同的具体问题会有不同的效果。
2.初识A*算法
启发式搜索其实有很多算法,比如局部择优搜索法、最好优先搜索法等。当然A*算法也是如此。这些算法都使用了启发函数,但在具体的选取最佳搜索节点时的策略不同。例如局部择优搜索法就是在搜索的过程中选取“最佳节点”后舍弃其他的兄弟节点和父亲节点,并且一直搜索下去。这种搜索的结果很明显,由于舍弃了其他的节点,可能也把最好的节点都舍弃了,因为求解的最佳节点只是在该阶段的最佳,并不一定是全局的最佳。最好优先法就“聪明”一些,在搜索时,没有舍弃节点(除非该节点是死节点),在每一步的估价中都把当前的节点和以前的节点的估价值比较得到一个“最佳的节点”。这样可以有效地防止丢失“最佳节点”。那么A*算法又是一种什么样的算法呢?其实A*算法也是一种最好优先的算法,只不过要加上一些约束条件。由于在一些问题求解时,我们希望能够求解出状态空间搜索的最短路径,也就是用最快的方法求解问题,这就是A*算法的任务。在此先下个定义,如果一个估价函数可以找出最短的路径,我们称之为可采纳性。A*算法是一个可采纳的最好优先算法A*算法的估价函数可表示为:

此处的f’(n)是估价函数,g’(n)是起点到终点的最短路径值,h’(n)是n到目标的最断路经的启发值。由于这个f’(n)其实是无法预先知道的,所以我们用前面的估价函数f(n)做近似。g(n)代替g’(n),但g(n)≥g’(n)才可(大多数情况下都是满足的,可以不用考虑),h(n)代替h’(n),但h(n)≤h’(n)才可(这一点特别重要)。可以证明应用这样的估价函数是可以找到最短路径的,也就是可采纳的。我们说应用这种估价函数的最好优先算法就是A*算法。
举一个例子,其实广度优先算法就是A*算法的特例。其中g(n)是节点所在的层数,h(n)=0这种h(n)肯定小于h’(n),所以由前述可知,广度优先算法是一种可采纳的但实际也是一种最差的A*算法。
接下来讲解有关h(n)启发式函数的信息式。h(n)的启发式信息通俗点说其实就是在估计一个节点的值时的约束条件,如果信息越多或约束条件越多则排除的节点就越多,估价函数就越好,或说这个算法越好。但在游戏开发中由于实时性的问题,h(n)的信息越多,它的计算量就越大,耗费的时间就越多。就应该适当减小h(n)的信息,即减小约束条件。但算法的准确性就差了,因为这里就有一个平衡的问题。
3.A*算法实现框架
在A*算法中的几个重要数据解释如下。
■ Open Table:存放所有已探知的但未搜索过点的优先队列。
■ Closed Table:存放搜索过的点的数组,提取最优路径时有用。
■ Start Node:起始点。
■ Target Node:终止点。
■ C Node:当前点。
提取最优路径的算法并不复杂,虽然在close表中会有许多无效的搜索点,但是最优路径上各结点的下标一定是按照close表中下标的升序排列的。因此,只要在close表中,将下标从终止点向起始点移动,若close[i+1]与close[i]没有关联,则剔除close[i]。
路径最优问题就是在两个结点之间找一条最短路径。肯定有读者禁不住要问,这个问题不是已经有Dijkstra算法可以解决了吗?是的,但是Dijkstra算法的复杂度是O(n2),一旦结点很多并且需要实时计算的话,Dijkstra算法就无法满足要求了。而A*处理这类有需要实时要求的问题则显得游刃有余。
在路径最优问题中,用来作为启发函数关键部分的h(n)其实很容易选,那便是当前节点至最终节点的距离,这个距离既可以是Hamilton距离(|x1-x2|+|y1-y2|),也可以是Euclid距离(直线距离)。都可以在较快的速度下达到问题的最优解。
4.深入A*算法
A*算法是最好优先算法的一种,只是有一些约束条件而已。接下来我们来看一看最好优先算法是如何编写的。在下面的图11-4中有如下状态空间。(https://www.xing528.com)
■ 起始位置是A。
■ 目标位置是P。
■ 字母后的数字表示节点的估价值。
在搜索过程中设置两个表,分别是OPEN和CLOSED。OPEN表保存了所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。算法
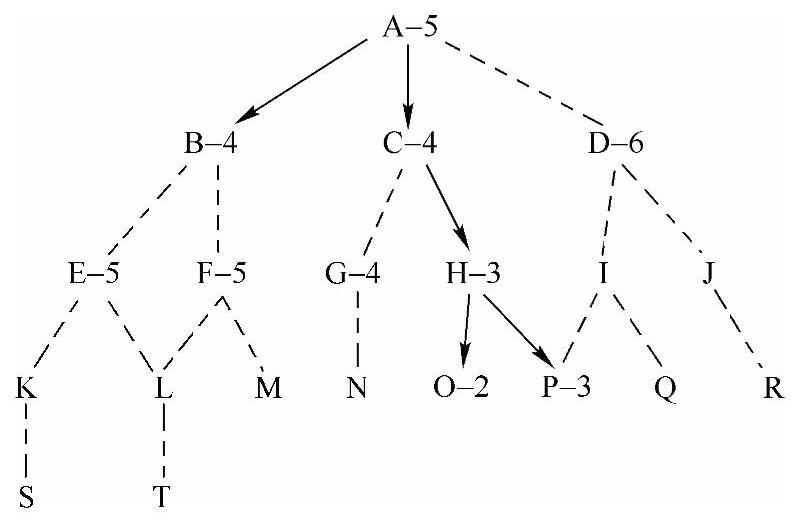
图11-4 A*算法过程
中有一步是根据估价函数重排OPEN表。这样循环中的每一步只考虑OPEN表中状态最好的节点即可。具体搜索过程如下。
(1)初始状态:
OPEN=[A5];CLOSED=[]。
(2)估算A5,取得所有子节点,并放入OPEN表中。
OPEN=[B4,C4,D6];CLOSED=[A5]。
(3)估算B4,取得所有子节点,并放入OPEN表中。
OPEN=[C4,E5,F5,D6];CLOSED=[B4,A5]。
(4)估算C4;取得所有子节点,并放入OPEN表中。
OPEN=[H3,G4,E5,F5,D6];CLOSED=[C4,B4,A5]。
(5)估算H3,取得所有子节点,并放入OPEN表中。
OPEN=[O2,P3,G4,E5,F5,D6];CLOSED=[H3,C4,B4,A5]。
(6)估算O2,取得所有子节点,并放入OPEN表中。
OPEN=[P3,G4,E5,F5,D6];CLOSED=[O2,H3,C4,B4,A5]。
(7)估算P3,已得到解。
看了上述具体过程后,接下来再看伪代码。此算法的伪代码如下。


具体的A*算法程序与上述程序是一样的,只要注意估价函数中的g(n)的h(n)约束条件就可以了。
5.用A*算法实现最短路径的搜索
在游戏设计中,经常涉及最短路径的搜索,现在一个比较好的方法就是用A*算法进行设计。A*算法的核心是估价函数f(n),它包括g(n)和h(n)两部分。g(n)是已经走过的代价,h(n)是n到目标的估计代价。g(n)可表示在状态空间从起始节点到n节点的深度,h(n)表示n节点所在地图的位置到目标位置的直线距离。一个是状态空间,一个是实际的地图。再详细点说有一个物体A,在地图上的坐标是(xa,ya),A所要到达的目标b的坐标是(xb,yb)。则开始搜索时,设置一个起始节点1,生成八个子节点2~9因为有八个方向。如图11-5所示。
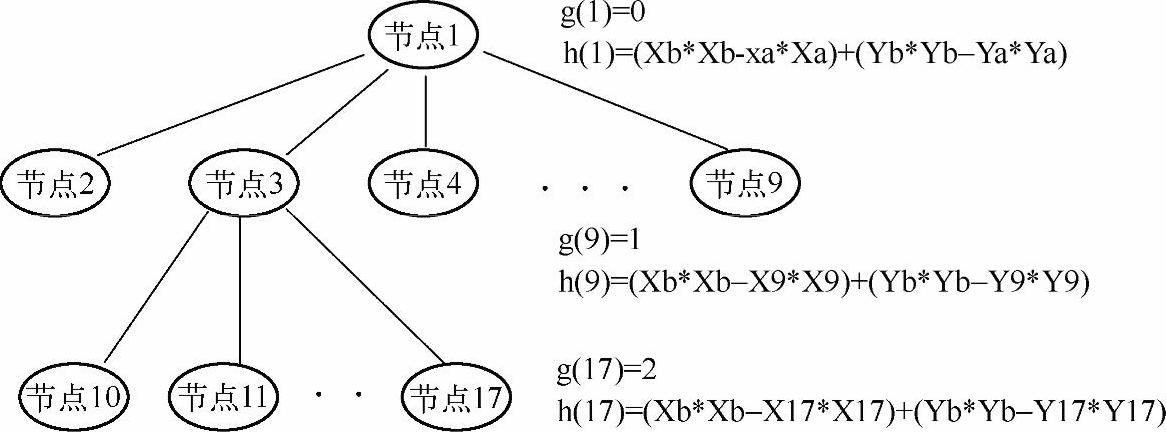
图11-5 节点图
读者需要仔细看节点1、9、17的g(n)和h(n)是怎么计算的。接下来开始讲解源程序,这个程序是一个很典型的程序,只要看懂了上面的伪代码,这个程序是十分容易理解的。
先看搜索主函数:

再看看生成子节点函数


接下来看最重要的A*算法函数


上述代码非常简单,编者已经在里面加上了详细的注释,请读者务必结合图11-4做到彻底了解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




