广度优先搜索算法(Breadth-First-Search),又译作宽度优先搜索,或横向优先搜索,简称BFS,是一种图形搜索算法。BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。广度优先搜索的实现一般采用open-closed表。图11-3展示了一个对节点进行广度优先搜索的处理顺序。
BFS是一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,而是彻底地搜索整张图,直到找到结果为止BFS并不使用经验法则算法。
从算法的观点来说,所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的操作里,其邻居节点尚未被检验过的节点会被放置在一个被称为open的容器中(例如队列或是链表),而被检验过的节点则被放置在被称为closed的容器中。
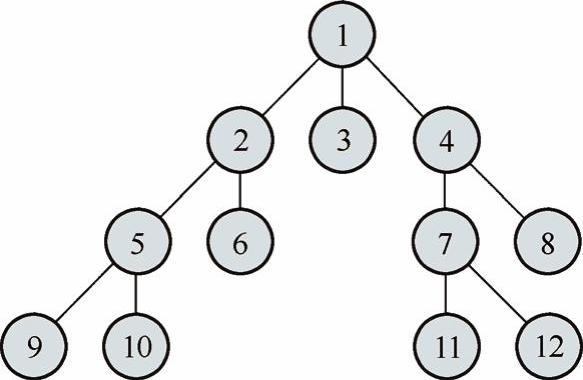
图11-3 对节点进行广度优先搜索的顺序
1.实现流程
(1)首先将根节点放入队列中。
(2)从队列中取出第一个节点,并检验它是否为目标。
■ 如果找到目标,则结束搜索并回传结果;
■ 否则将它所有尚未检验过的直接子节点加入队列中;
(3)如果队列为空,表示整张图都检查过了——即图中没有欲搜索的目标。结束搜索并回传“找不到目标”。
(4)重复步骤2。
2.复杂度
复杂度有两种,分别是空间复杂度和时间复杂度。
(1)空间复杂度(https://www.xing528.com)
因为所有节点都必须被储存,因此BFS的空间复杂度为O(|V|+|E|),其中|V|是节点的数目,而|E|是图中边的数目。还有另外一种说法是称BFS的空间复杂度为O(BM),其中B是最大分支系数,而M是树的最长路径长度。由于对空间的大量需求,因此BFS并不适合解非常大的问题。
(2)时间复杂度
在最差情形下,BFS必须寻找所有到可能节点的所有路径,因此其时间复杂度为O(|V|+ E|),其中|V|是节点的数目,而|E|是图中边的数目。
3.完全性
广度优先搜索算法具有完全性的特点,无论图形的种类如何,只要目标存在,则BFS一定会找到。但是如果目标不存在,并且图为无限大,则BFS将不会结束。
4.最佳解
如果所有边的长度相等,广度优先搜索算法是最佳解——即它找到的第一个解,距离根节点的边数目一定最少;但对一般的图来说,BFS并不一定得到最佳解。这是因为当图形为加权图(即各边长度不同)时,BFS仍然回传从根节点开始,经过边数目最少的解;而这个解距离根节点的距离不一定最短。要想解决这个问题,可以考虑使用BFS的改良算法—成本一致搜寻法(en:uniform-cost search)来解决。然而,若非加权图形,则所有边的长度相等,BFS就能找到最近的最佳解。
5.广度优先搜索算法的应用
在现实应用中,广度优先搜索算法可以解决图论中的如下问题。
(1)寻找图中所有连接元件(Connected Component),一个连接元件是图中的最大相连子图。
(2)寻找连接元件中的所有节点。
(3)寻找非加权图中任两点的最短路径。
(4)测试一图是否为二分图。
(5)(Reverse)Cuthill–McKee算法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




