进阶：深度优先搜索在Android游戏开发中的应用

深度优先搜索算法（Depth First Search，DFS）是图论搜索算法的一种，是指沿着树的深度遍历树的节点，尽可能深地搜索树的分支。当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到发现从源节点可达的所有节点为止如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个过程反复进行直到所有节点都被访问为止。属于盲目搜索。

深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便地解决很多相关的图论问题，如最大路径问题等。因发明“深度优先搜索算法”，霍普克洛夫特与塔扬共同获得计算机领域的最高奖——图灵奖。图11-1展示了一个对节点进行深度优先搜索的处理顺序。

深度优先算法，是计算机程序的一种编制原理，就是在一个问题有多种可以实现的方法和技术的时候，应该优先选择哪一个更合适的方法和技术，这种算法要用到计算机程序中的一种递归的思想。

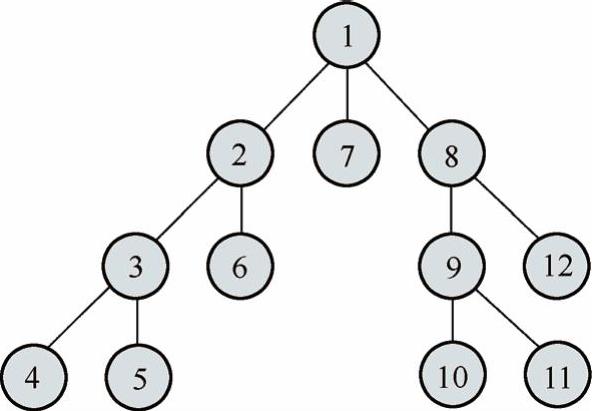
图11-1 对节点进行深度优先搜索的顺序

1.性质

依据深度优先搜索算法可以获得有关图结构的大量信息。深度优先搜索的最基本的特征是它的先辈子图G，形成一个由树组成的森林，这是因为深度优先树的结构准确反映了DFS_Visit中递归调用的结构的缘故，即u=π[v]当且仅当在搜索u的邻接表过程中调用了过程DFS_Visit(v)。

深度优先搜索的另一重要特性是发现和完成时间具有括号结构，如果我们把发现顶点u用左括号“（u”表示，完成用右括号“u）”表示，那么发现与完成的记载在括号被正确套用的前提下就是一个完善的表达式。例如，图11-2显示了深度优先搜索的性质。图11-2a对一个有向图进行深度优先搜索，节点的时间戳与边的类型的表示方式与图11-2b相同。图11-2b 中的括号表示对应于每个结点的发现时刻和完成时刻的组成的区间，每个矩形跨越相应节点的发现时刻与完成时刻所设定的区间，如果两个区间有重叠，则必有一个区间嵌套于另一个区间内，且对应于较小区间的节点是对应于较大区间的节点的后裔。图11-2c对图11-2a中的图重新描述，使深度优先树中所有树枝和正向边自上而下，而所有反向边自下而上从后裔指向祖先。

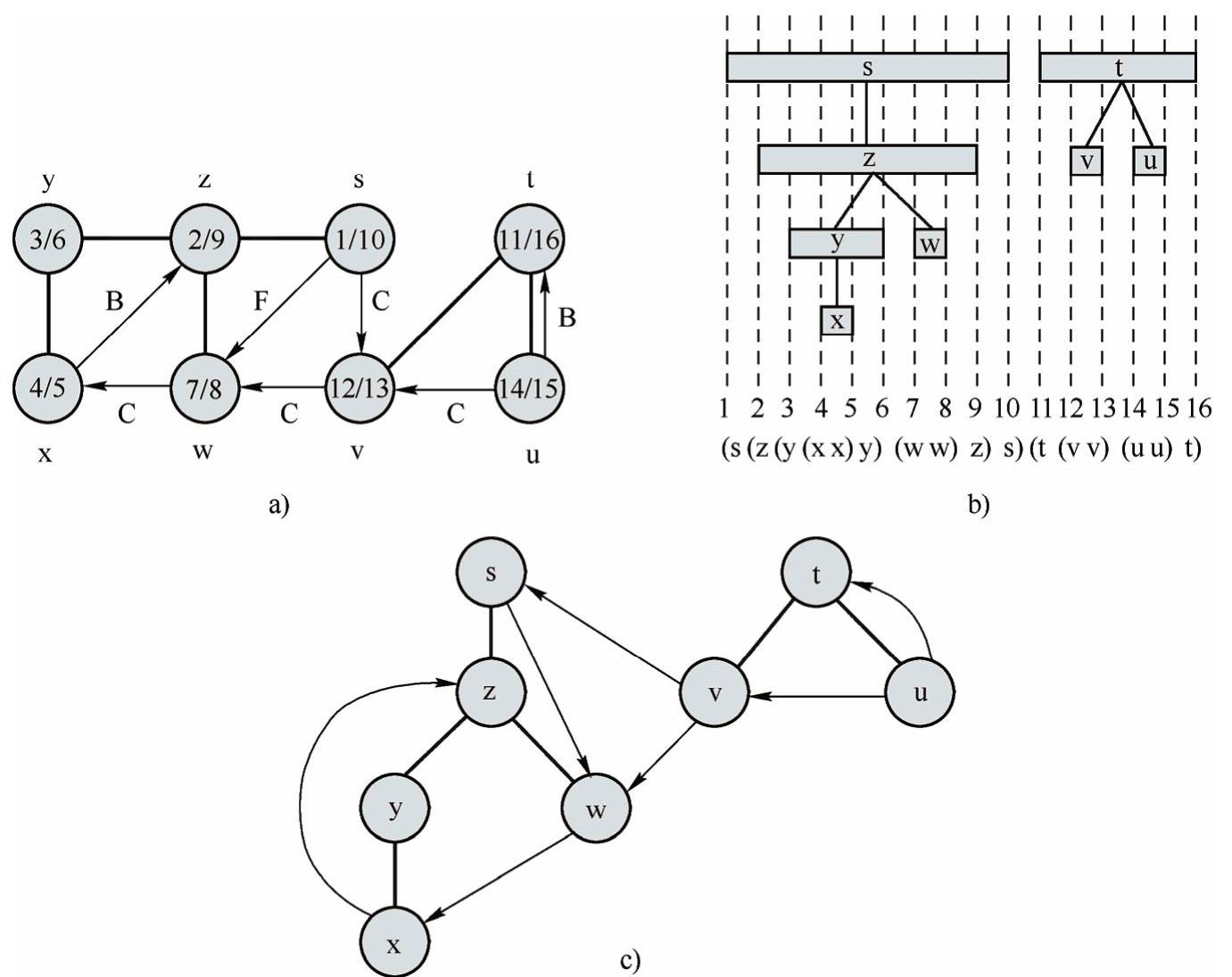
图11-2 深度优先搜索的性质

a)对一个有向图进行深度优先搜索 b)每个节点所处的对应区间 c)深度优先的只需过程

2.算法流程

含有深度界限的深度优先搜索算法的基本实现流程如下。

（1）把起始节点S放到未扩展节点OPEN表中。如果此节点为一目标节点，则得到一个解。

（2）如果OPEN为一空表，则失败退出。

（3）把第一个节点(节点n)从OPEN表移到CLOSED表。

（4）如果节点n的深度等于最大深度，则转向（2）。(www.xing528.com)

（5）扩展节点n，产生其全部后裔，并把它们放入OPEN表的前头。如果没有后裔，则转向（2）。

（6）如果后继节点中有任一个为目标节点，则求得一个解，成功退出；否则，转向（2）

3.经典问题

深度优先算法最经典的应用是解决迷宫问题和八皇后问题。

（1）迷宫问题

一只老鼠，从一座不见天日的迷宫的入口进去，要从出口出来。那老鼠会怎么走？当然是这样的：老鼠如果遇到直路，就一直往前走，如果遇到分叉路口，就任意选择其中的一个继续往下走，如果遇到死胡同，就退回到最近的一个分叉路口，选择另一条道路再走下去，如果遇到了出口，老鼠的旅途就算结束了。深度优先搜索法的基本原则就是这样：按照某种条件往前试探搜索，如果前进失败（正如老鼠遇到死胡同），则退回另选通路继续搜索，直到找到符合条件的目标为止。

■ 递归算法

要想实现这一算法，我们要用到编程的一大利器——递归。虽然“递归”是一个很抽象的概念，但是在日常生活中会经常看到。请读者朋友拿两面镜子，把它们面对着面，会看到什么？会看到镜子中有无数个“镜中镜”。A镜子中有B镜子的像，B镜子中有A镜子的像A镜子的像就是A镜子本身的真实写照，也就是说A镜子的像包括了A镜子，还有B镜子在A镜子中的像等。如果换成计算机语言就是A调用B，而B又调用A，这样间接的，A就调用了A本身，这实现了一个重复的功能。

■ 解法

我们把递归思想运用到上面的迷宫中，记老鼠现在所在的位置是（x,y），那它现在有前后左右4个方向可以走，分别是(x+1,y),(x-1,y),(x,y+1),(x,y-1)，其中一个方向是它来时的路先不考虑，先分别尝试其他三个方向，如果某个方向是路而不是墙的话，老鼠就向那个方向在新的位置上，又可以重复前面的步骤。若老鼠走到了死胡同，就是除了来时的路，其他3个方向都是墙，这时这条路就走到了尽头，无法再向深一层前进，就应该沿来时的路回去，尝试另外的方向。

（2）八皇后问题

■ 八皇后问题描述

在国际象棋中，皇后的威力是最大的，既可以横走竖走，还可以斜着走，遇到挡在她前进路线上的敌人就可以直接吃掉。要求在标准的国际象棋棋盘上（8×8格）放置8只皇后，使她们彼此都不能吃到对方，求皇后的放法。

■ 解法

这是一个很经典的问题，我们先要明确一下思路，如何运用深度优先搜索法来完成这道实例。我们先建立一个8×8格的棋盘，在棋盘的第一行的任意位置安放一只皇后。紧接着放第二行，第二行的安放就要受一些限制了，因为与第一行的皇后在同一竖行或同一对角线的位置上是不能安放皇后的。接下来是第三行……或许我们会遇到这种情况，在摆到某一行的时候，无论皇后摆放在什么位置，她都会被其他行的皇后吃掉，这说明什么呢？这说明前面的摆放是失败的，也就是说，按照前面的皇后的摆放方法，不可能得到正确的解。那这时怎么办？答案是继续修改！回到上一行，把原先摆好的皇后换另外一个位置，接着再回过头摆这一行，如果这样还不行或者上一行的皇后只有一个位置可放，那怎么办？那就回到上一行的上一行……这和老鼠碰了壁就回头是一个意思。就这样不断尝试，修正，最终会得到正确的结论。