悬臂梁(材料为铝,密度为2700kg/m3;杨氏模量为70GPa;泊松比为0.33)左端固支,右端受力P=1N,如图2-8所示。求梁右端的挠度、最大弯曲应力、前3阶横向振动模态频率(x-z平面内),并与有限元解对比。
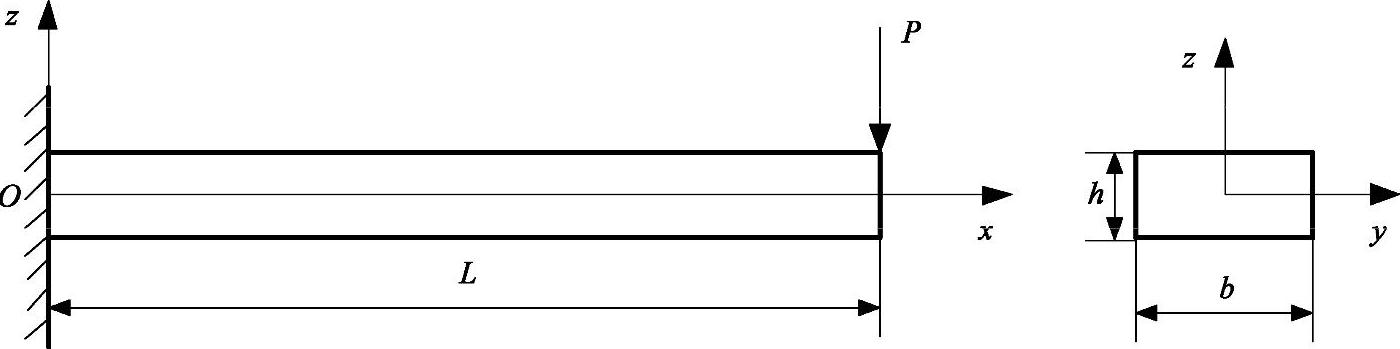
图2-8 右端受载的悬臂梁
图2-8中,三为梁的长度;h和6为梁的横截面尺寸。梁右端的挠度Vmax可由式(2-9)[8]

给出。式中,E为杨氏模量;Iy为y轴惯性矩,且可表达为

由于梁在O点的弯矩最大,最大弯曲应力σ必然出现在O点的上下边缘,即

式中,M为弯矩。
由弹性振动理论,悬臂梁横向振动(图2-8中的x-z平面)前3阶固有频率的理论解为[9]

式中,fn为第n阶固有频率;ρ为材料密度;A=bh为梁的横截面面积;an为系数,且有a1=1.8751,a2=4.6941,a3=7.8548。
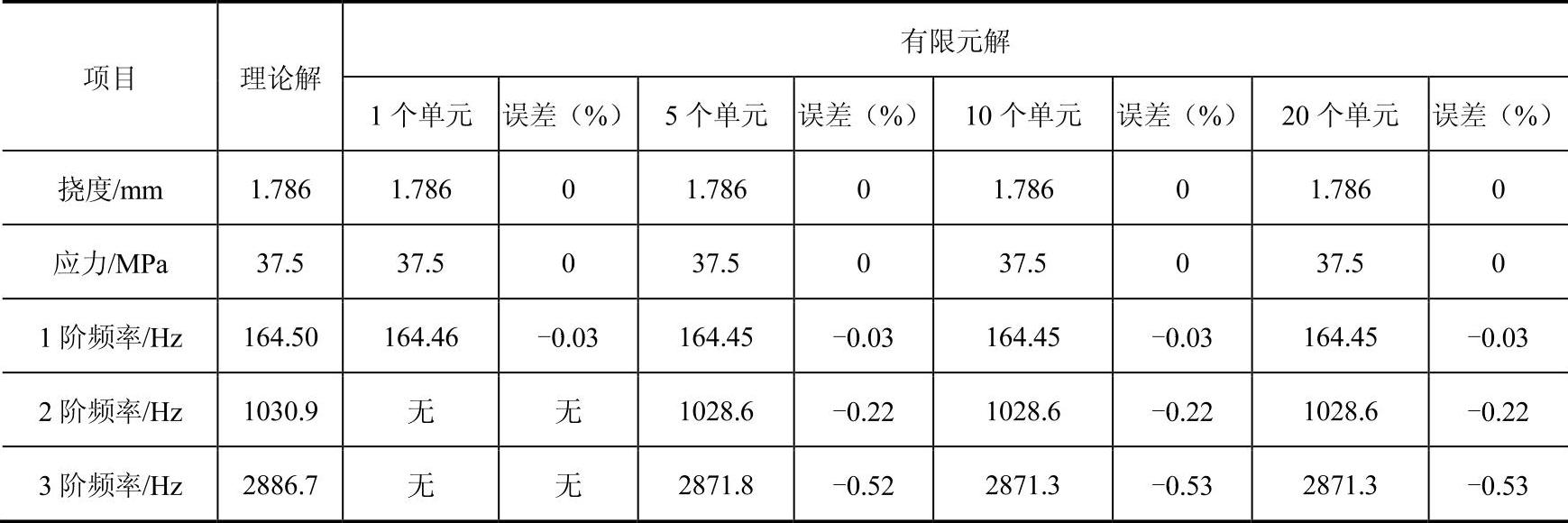
令L=100mm,h=2mm,b=4mm,P=1N,并将参数代入式(2-9)~式(2-12)中,即可求出vmax、σ以及前3阶模态频率,列于表2-3中。为方便与有限元解进行比较,表2-3也列出了有限元解。
表2-3 有限元解与理论解的对比
计算及结果说明:
1)对于BEAM188单元,设置单元选项K3=3(Cubic Form),有助于提高计算精度。
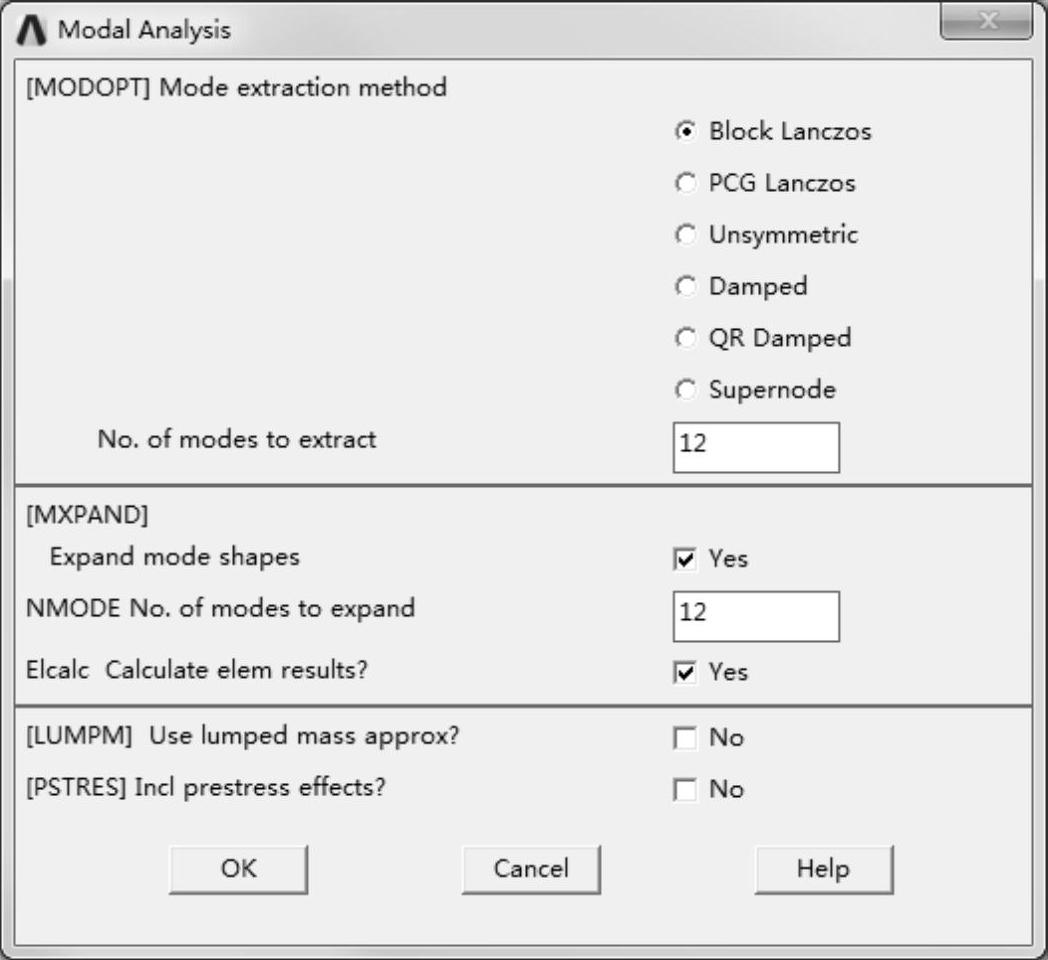
2)为便于观察模态变形,将计算单元结果(Calculate elem results)选项开启,设置方法如图2-9所示。
3)约束固支端节点的6个自由度。除x-z平面内的振动外,悬臂梁还产生x-y平面内的振动、绕x轴的扭振以及沿x轴向的振动,本例不做深入研究。
 (https://www.xing528.com)
(https://www.xing528.com)
图2-9 Modal Analysis对话框
4)BEAM188单元可以显示横截面形状(/ESHAPE,1)。因此,可直接在应力云图中观察梁的应力分布状态,而无需进行定义单元表等复杂操作。对于本例,x方向的应力即为梁横截面的弯曲应力,如图2-10所示。应力在横截面内沿高度方向呈线性变化,与理论吻合。
说明:ANSYS计算的应力、应变均以单元坐标系表示,位移、支反力等以节点坐标系(默认平行于总体笛卡儿坐标系)表示。
5)y、z方向应力,xy、yz、xz剪应力均为零,第一主应力(σ1)云图如图2-11所示,第二主应力(σ2)为零,第三主应力(σ3)云图如图2-12所示。von Mises应力(σe)与主应力之间的关系由式(2-13)表达。因此,von Mises应力云图如图2-13所示。对于本例的梁单元,x方向应力、第一主应力和第三主应力绝对值的最大值均完全相同,这是因为梁单元横截面只有一个节点,可精确模拟梁弯曲问题。
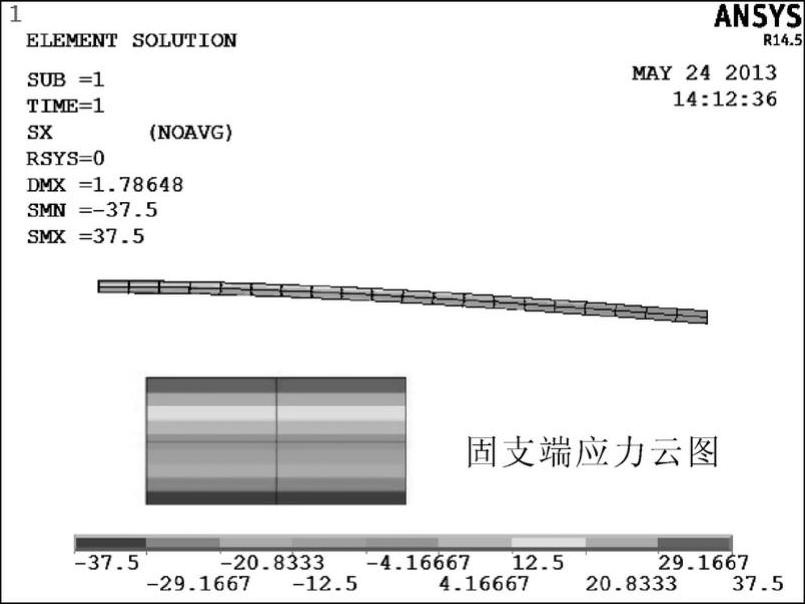
图2-10 x方向的应力云图

图2-11 固支端的第一主应力云图

图2-12 固支端的第三主应力云图
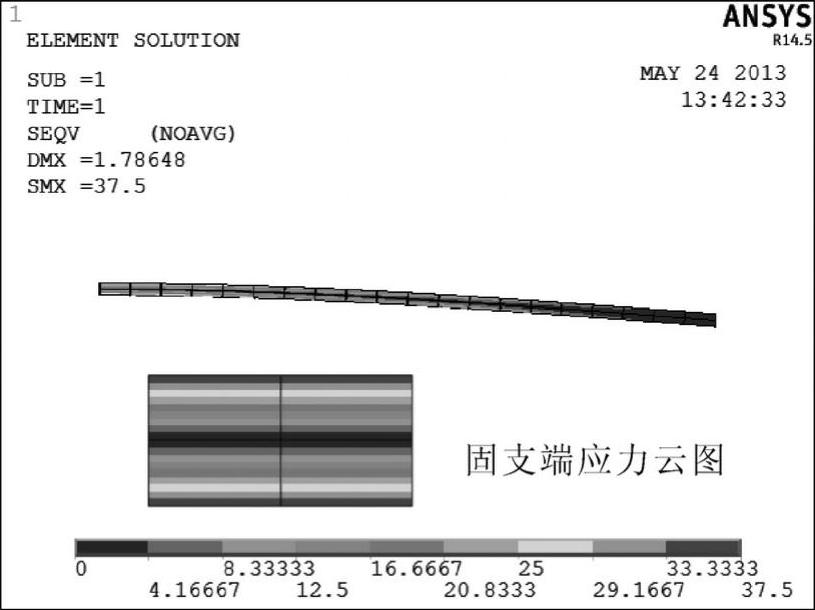
图2-13 von Mises应力云图
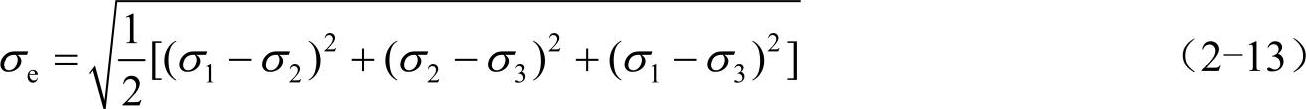
6)对于仅含有1个梁单元的模型,也可得出准确的结果,但只能计算x-z平面内的1阶模态,这是由系统自由度决定的。图2-14和图2-15分别为5个梁单元、20个梁单元的前3阶模态振型,与理论预测完全一致。

图2-14 5个梁单元的前3阶模态振型
a)1阶模态 b)2阶模态 c)3阶模态

图2-15 20个梁单元的前3阶模态振型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




