一、选择题
答案
(1)如果取L1为y=f(x)的图形,则f′(x)>0(x∈(0,x2)),f′(x)<0(x∈(x2,x4)),f′(x)>0(x∈(x4,a)),这与L2为y=f′(x)图形相符,也与L3为y=∫xf(t)dt的图
0形相符.所以选(A).
附注 本题是先选定L1为y=f(x)的图形,然后检验L2,L3是否分别为y=f′(x),y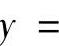
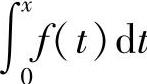 的曲线.如果如此选定不行,则再考虑L2为y=f(x)的图形,等等,直到得到正确选项为止.
的曲线.如果如此选定不行,则再考虑L2为y=f(x)的图形,等等,直到得到正确选项为止.
(2)当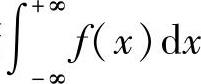 收敛时,有
收敛时,有
所以选(C).
附注 当f(x)在(-∞,+∞)上连续,且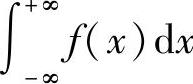 收敛时有
收敛时有
(3)由于S关于平面x=0对称,x在对称点处的值互为相反数,所以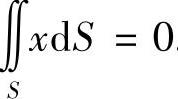 .由于D关于x轴对称,y在对称点处的值互为相反数,所以
.由于D关于x轴对称,y在对称点处的值互为相反数,所以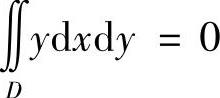 ,因此选(C).
,因此选(C).
附注 当曲面S关于某个坐标平面对称时,如果被积函数f(x,y,z)在对称点处的值彼此相等(或互为相反数),则
其中,S1是S被此坐标平面划分成的两部分之一.
记住这一结论,往往能化简关于面积的曲面积分的计算.
(4)容易看到y2-y1=e-x(cosx+sinx)是y″+py′+qy=0的特解,所以
p=-[(-1+i)+(-1-i)]=2,q=(-1+i)(-1-i)=2.
此外,由题设知ex是y″+py′+qy=f(x),即y″+2y′+2y=f(x)的特解,所以
f(x)=(ex)″+2(ex)′+2ex=5ex.
因此选(A).
附注 容易知道,e-xcosx是y″+2y′+2y=0的解,所以由题设知ex是y″+2y′+2y=f(x)的解.
(5)由于ATAx=0与Ax=0是同解方程组,所以ξ1,ξ2必是ATAx=0的基础解系.由于Ax=0与Bx=0都有基础解系ξ1,ξ2,所以ξ1,ξ2也是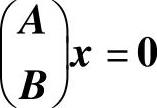 的基础解系,因此选(B).
的基础解系,因此选(B).
附注 ξ1,ξ2未必是A+B的基础解系,例如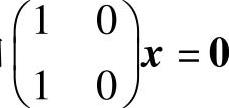 和
和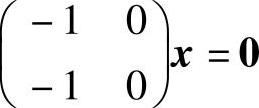 有相同的基础解系(0,1)T,但它不是
有相同的基础解系(0,1)T,但它不是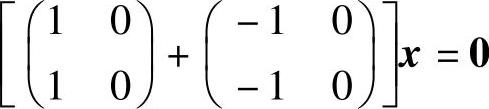 的基础解系,所以(A)与(D)都不能选.
的基础解系,所以(A)与(D)都不能选.
ξ1,ξ2也未必是B∗x=0的基础解系,例如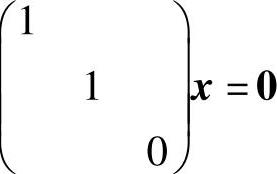 有基础解系(0,0,1)T,但它不是
有基础解系(0,0,1)T,但它不是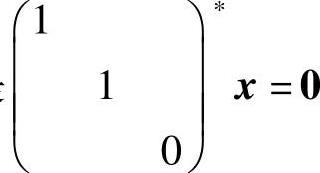 的基础解系,这是因为
的基础解系,这是因为 的秩为2=3-1,所以
的秩为2=3-1,所以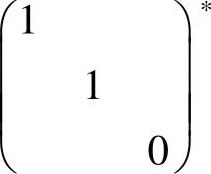 的秩为1,从而
的秩为1,从而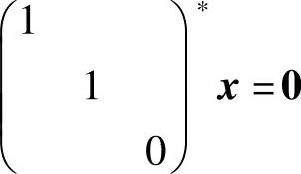 的基础解系中应有两个线性无关的解向量.因此(C)不能选.
的基础解系中应有两个线性无关的解向量.因此(C)不能选.
(6)实对称矩阵A,B合同的充分必要条件是分别以A,B为矩阵的二次型有相同的规范形.因此选(D).
附注 (Ⅰ)选项(A)是A与B合同的必要条件而不是充分条件,而选项(B)、(C)既不是必要条件,也不是充分条件.
(Ⅱ)两个n阶实对称矩阵A,B合同的充分必要条件有两种:
(i)A,B的特征值分别相等(当某个特征值k重时,按k个计算);
(ii)以A,B为矩阵的二次型有相同的规范形.
(7)F(1,4)=P(X≤1,Y≤4)=P(X≤1,X2≤4)=P(-2≤X≤1)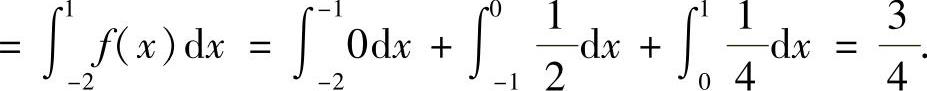
因此选(C).
附注 顺便计算X的分布函数G(x)=P(X≤x).
当x≤-1时,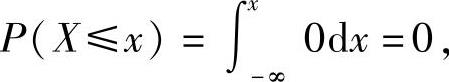
当-1<x<0时,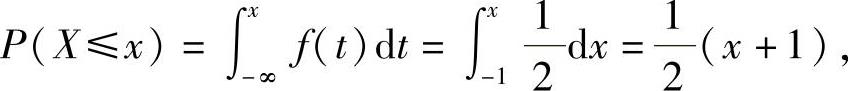
当0≤x≤2时,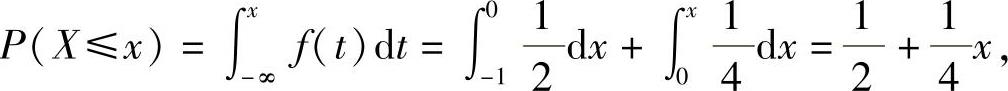
当x>2时,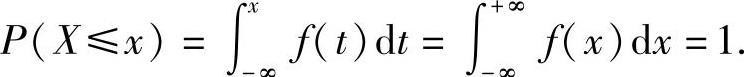
所以,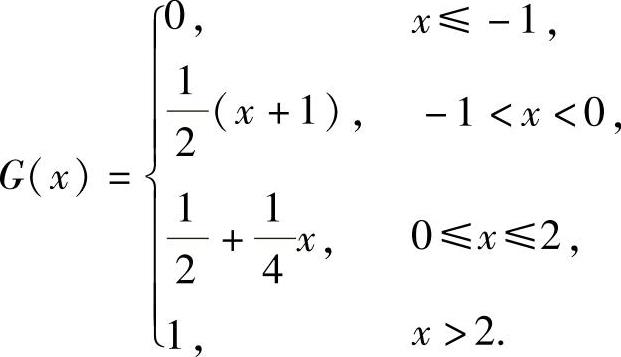
(8)由于随机变量t的概率密度曲线关于纵轴对称,所以由
α=P(|t|≤b)=1-P(|t|>b)=1-P(t>b)-P(t<-b)=1-2P(t>b)得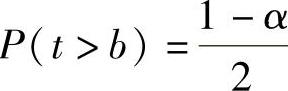 ,从而由tα(n)的定义得
,从而由tα(n)的定义得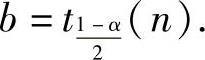
因此选(C).
附注 应当记住:
当X~N(0,1)时,满足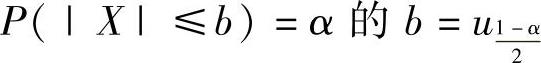 (其中,uα为满足P(X>uα)=α的实数);
(其中,uα为满足P(X>uα)=α的实数);
当X~T(n)时,满足P(|X|≤b)=α的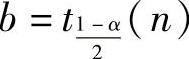 (其中,tα(n)为满足P(X>tα(n))=α的实数).
(其中,tα(n)为满足P(X>tα(n))=α的实数).
二、填空题
(9)所给微分方程可改写成
它的通解为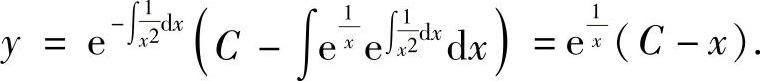
将y(1)=0代入得C=1,所以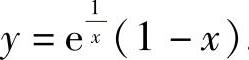 .从而由
.从而由
得曲线y=y(x)的斜渐近线方程为y=-x.
附注 计算曲线y=f(x)的斜渐近线方程时,总是先计算
如果这两个极限中至少有一个不存在,则计算
和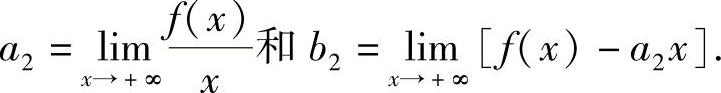
(10)由于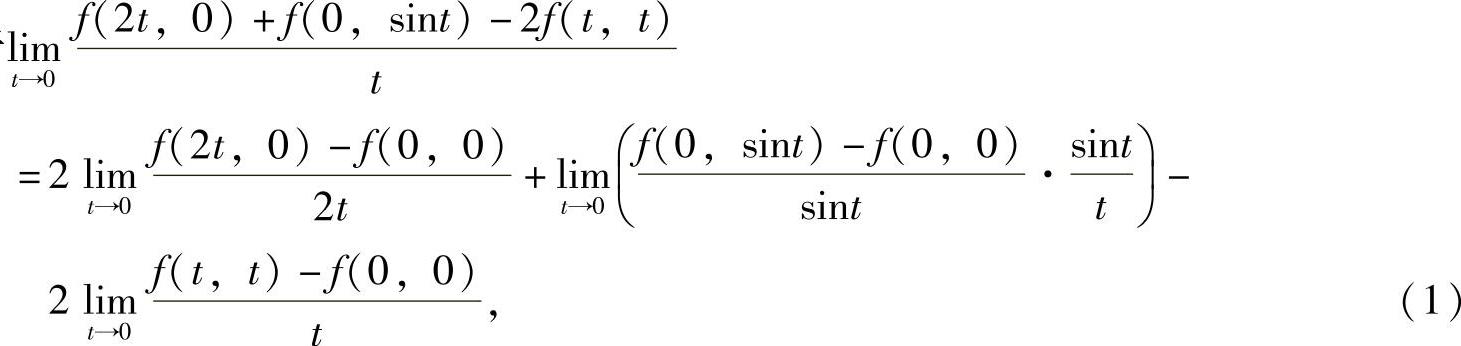
其中,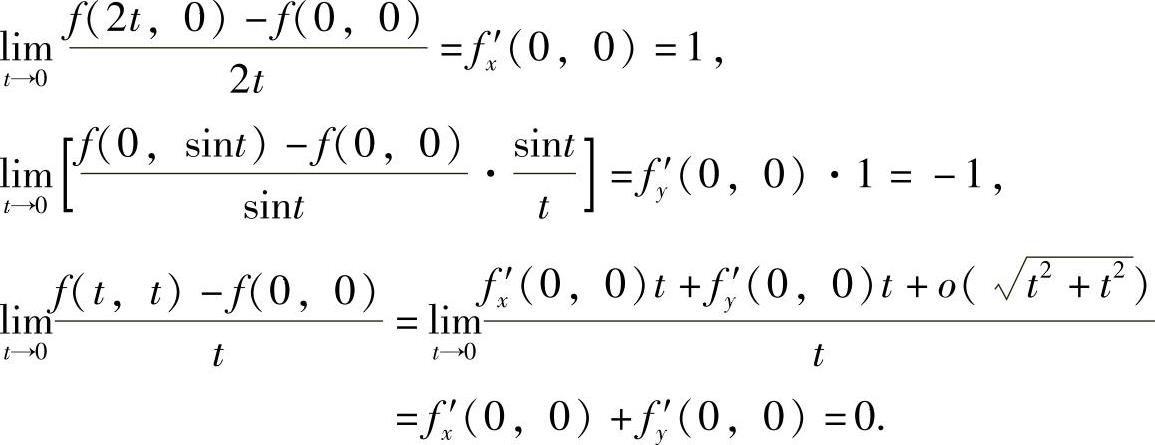
将它们代入式(1)得
附注 由于f(x,y)仅在点(0,0)处可微,所以需用偏导数的定义与全微分的定义计算本题的极限.
(11)平面z=1被Σ所截下的有限部分上侧记为S,它在xOy平面的投影为D={(x,y)|x2+y2≤1},则由高斯公式有
附注 由于题中的Σ不是闭曲面,所以添上一块S,构成闭曲面,然后应用高斯公式计算所给的曲面积分.这是计算关于坐标的曲面积分的常用方法.
(12)f(x)的麦克劳林展开式为
附注 (Ⅰ)写出f(x)的泰勒展开式或麦克劳林展开式时,应写出泰勒级数或麦克劳林级数的通项,还应写出展开式的成立范围.
(Ⅱ)初等函数的麦克劳林展开式总是用间接法计算,即利用常用函数ex,sinx,cosx,ln(1+x)及(1+x)μ的麦克劳林展开式及幂级数的加、减运算和求导、积分运算等计算.
(13)由r(A)+r(B)-3≤r(AB)得r(A)≤2,所以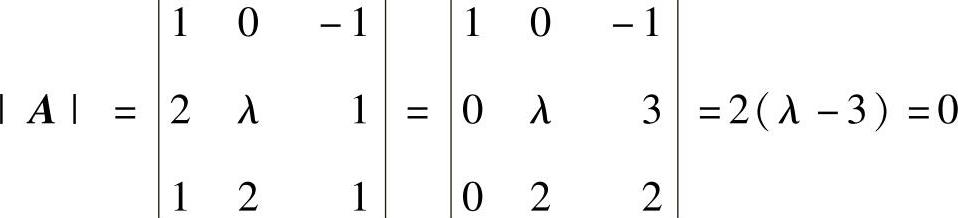 ,由此得到λ=3.
,由此得到λ=3.
附注 应记住关于矩阵秩运算的以下两个公式:
(Ⅰ)设A,B都是m×n矩阵,则
r(A+B)≤r(A)+r(B).
(Ⅱ)设A,B分别是m×n和n×l矩阵,则
r(A)+r(B)-n≤r(AB)≤min{r(A),r(B)}.
(14)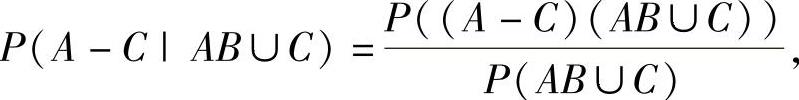
其中,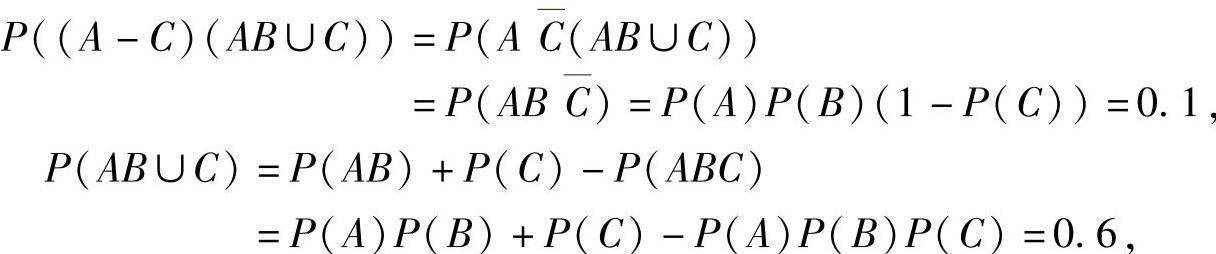
所以,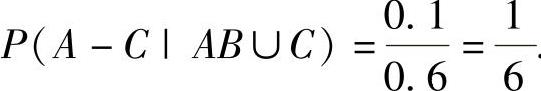
附注 对于比较复杂的随机事件概率,总是利用简单的随机事件概率和概率计算公式计算.概率计算公式主要有
设A,B都是事件,则
P(A)=1-P(A)(逆概公式);
P(A∪B)=P(A)+P(B)-P(AB)(加法公式);
特别当A,B互不相容时,P(A∪B)=P(A)+P(B);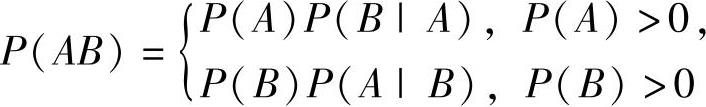 (乘法公式);
(乘法公式);
设A1,A2,…,An是一个完全事件组,则当P(Ai)>0(i=1,2,…,n)时,对任意随机事件B有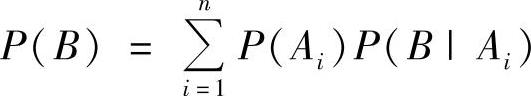 (全概率公式).
(全概率公式).
三、解答题
(15)由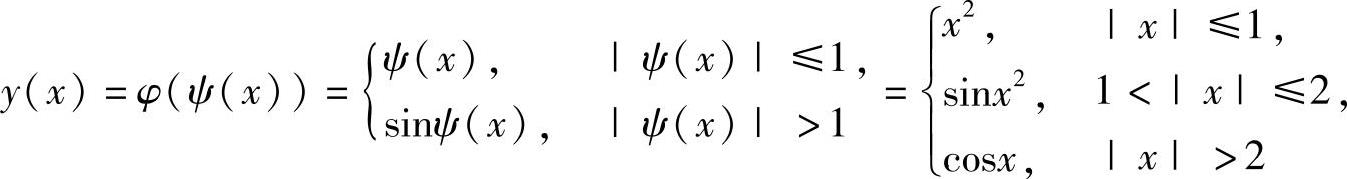 知,
知,
|x|<1时,y′(x)=2x;
1<|x|<2时,y′(x)=2xcosx2;
|x|>2时,y′(x)=-sinx.
并且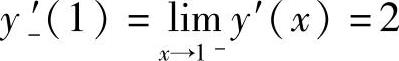 ,
,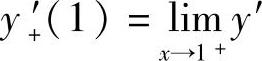 (x)=2cos1,
(x)=2cos1,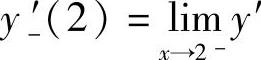 (x)=4cos4,
(x)=4cos4,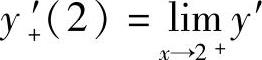 (x)=-sin2,
(x)=-sin2,
所以y′(x)在点x=1,2处不存在,由于f(x)是偶函数,所以y′(x)在点x=-1,-2处也不存在,从而
因此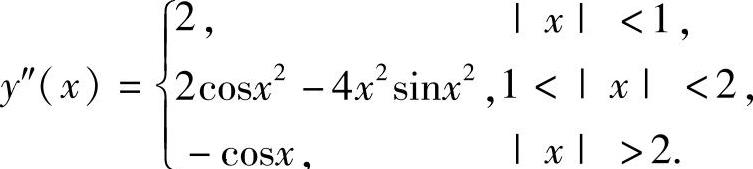 (https://www.xing528.com)
(https://www.xing528.com)
附注 本题的题解有两点值得注意:
(Ⅰ)要计算分段函数复合函数的导数,应先算出复合函数的表达式.
(Ⅱ)对分段函数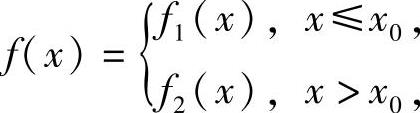 如果已算出f′1(x)(x<x0)与f′2(x)(x>x0),则当
如果已算出f′1(x)(x<x0)与f′2(x)(x>x0),则当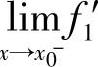 (x)与
(x)与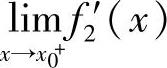 都存在时,
都存在时,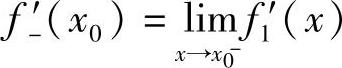 ,
,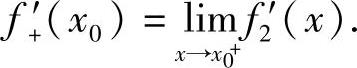
(16)因为f(x)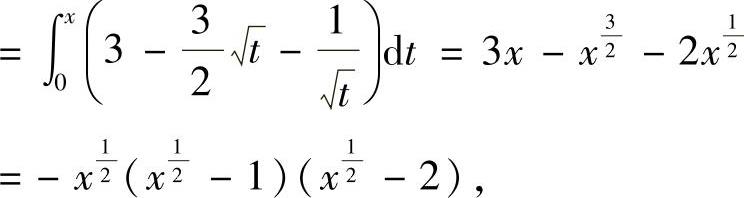
并且x∈(0,1)∪(4,+∞)时f(x)<0,x∈(1,4)时f(x)>0以及f(0)=f(1)=f(4)=0,
所以y=f(x)(x≥0)的图形如图答9-16所示,因此,所求的面积为
图答 9-16
附注 计算平面图形的面积时,应先画出该图形.
当平面图形D是由曲线y=f1(x),y=f2(x)(f1(x),f2(x)在[a,b]上连续)及直线x=a,x=b围成,则D的面积
本题的平面图形可理解为是由曲线y=f(x),直线y=0,x=0,x=4围成的,所以
(17)由于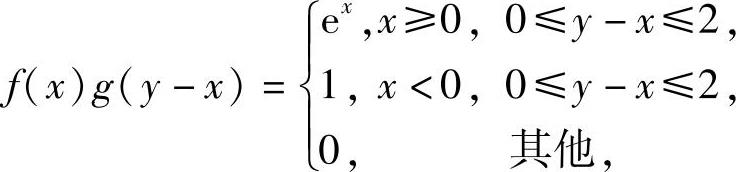
所以,f(x)g(y-x)仅在图答9-17阴影部分取非零值,而在xOy平面的其他部分都取零值.因此
图答 9-17
其中,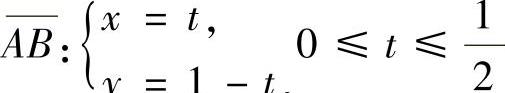 ,所以
,所以
将它们代入式(1)得
附注 关于弧长的平面曲线积分计算公式是:
设f(x,y)是连续函数,曲线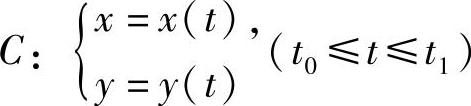 ,其中x(t),y(t)在[t0,t1]上具有连续的导数,则
,其中x(t),y(t)在[t0,t1]上具有连续的导数,则
(18)(Ⅰ)利用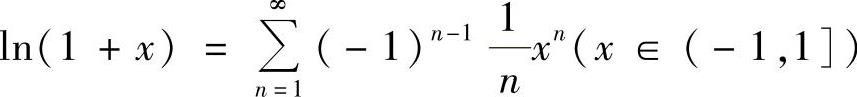 得
得
(Ⅱ)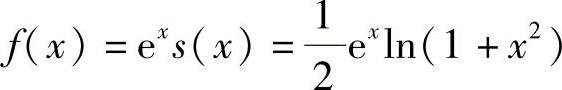 在[-1,1]上连续,在(0,1)内可导且
在[-1,1]上连续,在(0,1)内可导且
显然在(0,1)内f′(x)>0,且f′(0)=0.下面证明在(-1,0)内f′(x)<0.记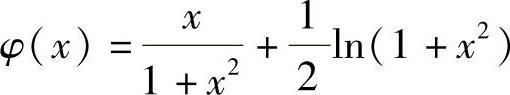 ,则φ(x)在(-1,0)内可导且
,则φ(x)在(-1,0)内可导且
记ψ(x)=x3-x2+x+1,则ψ′(x)=3x2-2x+1>0(x∈(-1,0)),且ψ(-1)<0,ψ(0)>0,所以存在x0∈(-1,0),使得
由此得到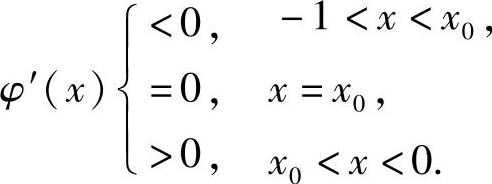
于是,由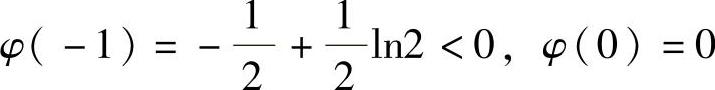 知φ(x)<0,即f′(x)<0(x∈(-1,0)).
知φ(x)<0,即f′(x)<0(x∈(-1,0)).
由此得到f(x)在<-1,1)内有唯一驻点x=0,于是f(x)在[-1,1]上的最大值为max{f(0),f(-1),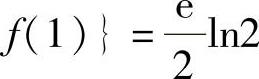 ,最小值为min{f(0),f(-1),f(1)}=0.
,最小值为min{f(0),f(-1),f(1)}=0.
附注 解本题(Ⅱ)的关键是证明f′(x)<0(x∈(-1,0)),即证明不等式
题解中采用了导数方法.
(19)由于f(ξ)+ξf′(ξ)=0即为[xf(x)]′x=ξ=0.所以作辅助函数F(x)=xf(x),它在[0,1]上连续,在(0,1)内可导,且由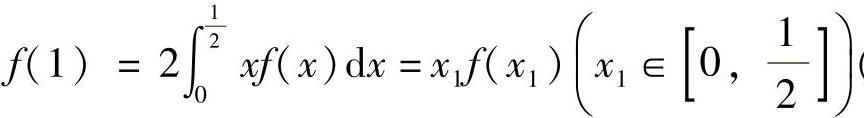 (根据积分中值定理)
(根据积分中值定理)
知F(1)=F(x1),所以由罗尔定理知,存在ξ∈(x1,1)⊂(0,1),使得F′(ξ)=0,即f(ξ)+ξf′(ξ)=0.
附注 题解中综合使用了罗尔定理与积分中值定理.
(20)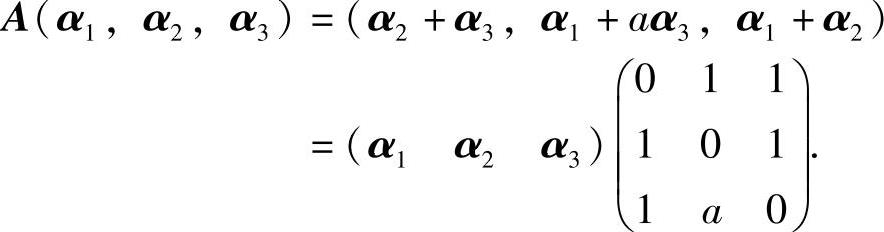
记 P=(α1,α2,α3),则P可逆,且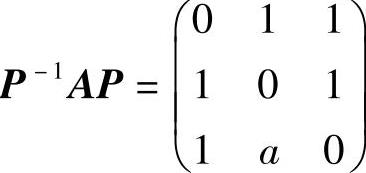 ,即
,即
则由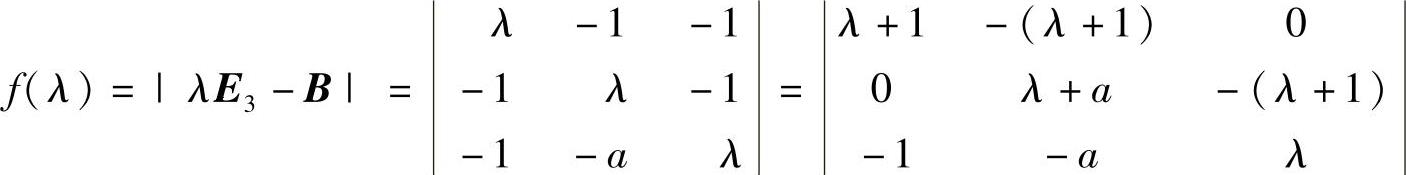
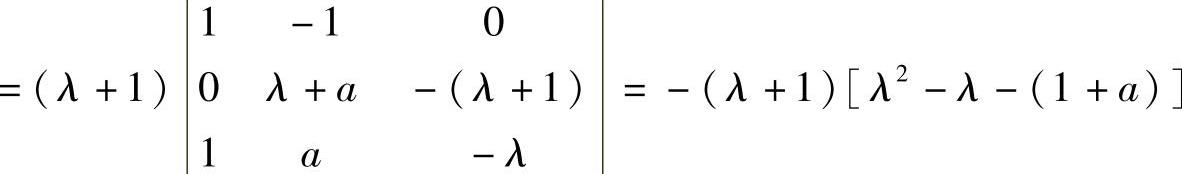 知
知
方程f(λ)=0不可能有三重根,这是因为如果λ=-1是三重根,则λ=-1是λ2-λ-(1+a)=0的二重根;但是当λ=-1是λ2-λ-(1+a)=0的根时a=1,此时λ2-λ-(1+a)=0成为λ2-λ-2=0,这与λ=-1是它的二重根矛盾.
方程f(λ)=0有二重根时,应分两种情形讨论:
(ⅰ)λ=-1是方程的二重根,则由以上计算此时a=1,并且由
知r(-E3-B)=1=3-2(即矩阵B的阶数与λ=-1的重数之差),所以此时B可相似对角化.由于A~B,所以此时A可相似对角化.
(ⅱ)λ=-1不是方程的二重根时,方程λ2-λ-(1+a)=0必有二重根,从而(-1)2-4[-(1+a)]=0,即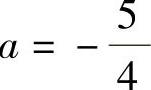 ,并且此时的二重特征根为
,并且此时的二重特征根为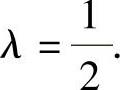 由
由
知,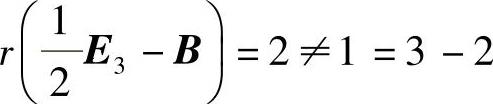
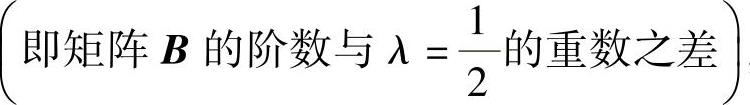 ,所以此时B不可相似对角化,从而A不可相似对角化.
,所以此时B不可相似对角化,从而A不可相似对角化.
综上所述,当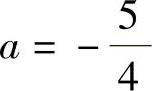 时,A不可相似对角化.
时,A不可相似对角化.
附注 设A是n阶矩阵,则A可相似对角化的充分必要条件有下列两种:
(Ⅰ)A有n个线性无关的特征向量;
(Ⅱ)A的每个特征值λi(即特征方程|λEn-A|=0的根),都满足
r(λiEn-A)=n-ni (ni是λi的重数).
本题的求解是利用第(Ⅱ)种充分必要条件.
(21)(Ⅰ)由题设知,A有特征值λ1=2,λ2=λ3=-1.从而λ1对应A∗的特征值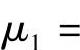
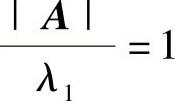 ,所以由A∗α=α知μ1=1对应的特征向量为α=(1,1,-1)T,由此可知A的对应λ1=1的特征向量为α.
,所以由A∗α=α知μ1=1对应的特征向量为α=(1,1,-1)T,由此可知A的对应λ1=1的特征向量为α.
设λ2=λ3=-1对应的特征向量为β=(b1,b2,b3),则由A是实对称矩阵知β与α正交,即
b1+b2-b3=0.
故可取β为它的基础解系,即
β1=(-1,1,0)T, β2=(1,0,1)T.现将它们正交化:
γ1=β1=(-1,1,0)T,
显然,α,γ1,γ2是正交向量组,现将它们单位化得
于是所求的正交矩阵为Q=(ξ1,ξ2,ξ3),它使
所以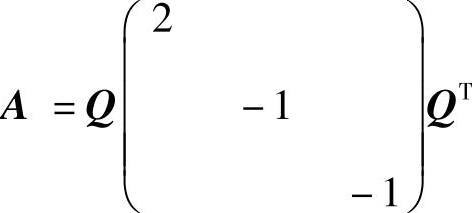
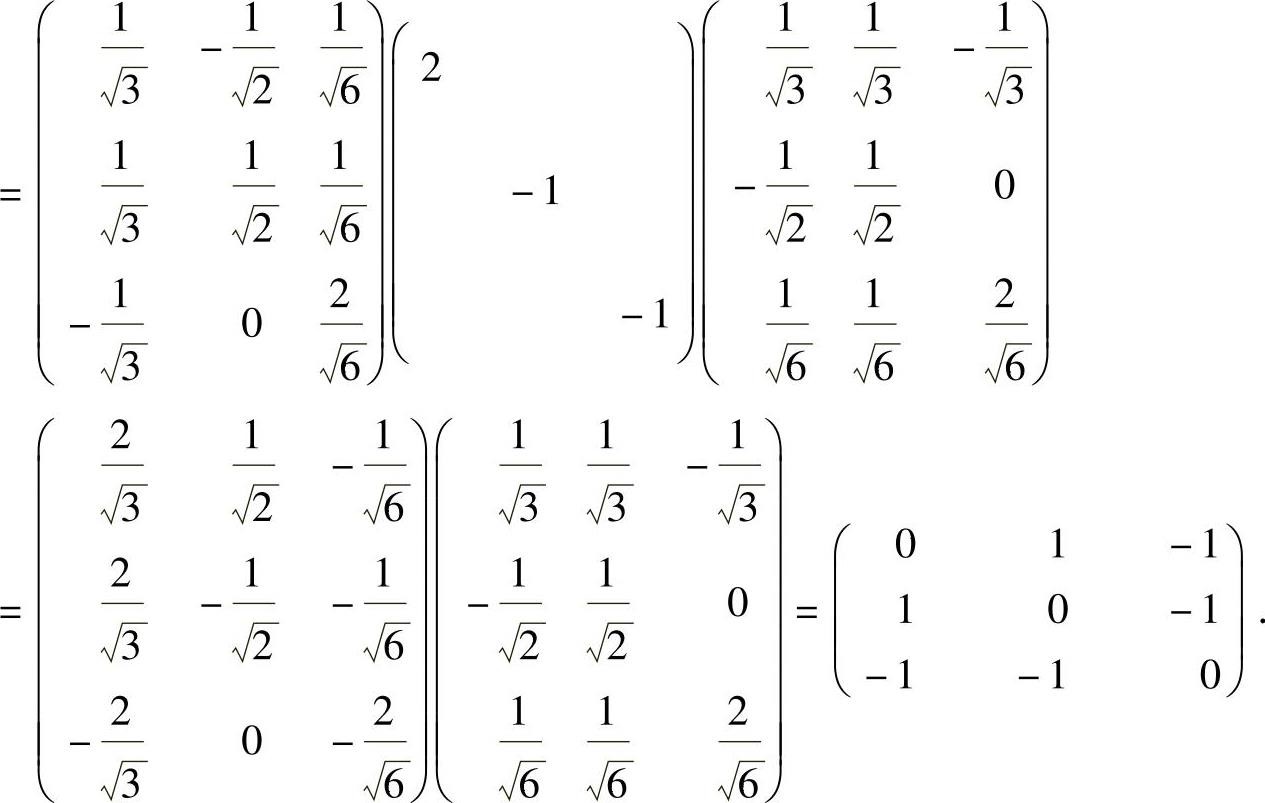
(Ⅱ)由于f(x1,x2,x3)在正交变换x=Qy下的标准形为2y21-y22-y23,
故令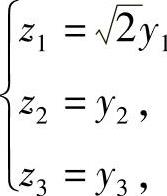 ,即
,即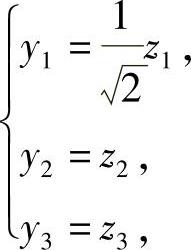 或
或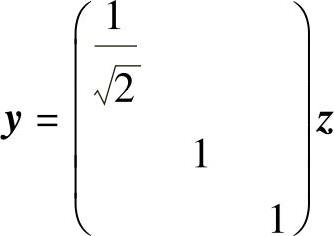 ,则
,则
2y21-y22-y23=z21-z22-z23(规范形).
从而f(x1,x2,x3)在可逆线性变换
即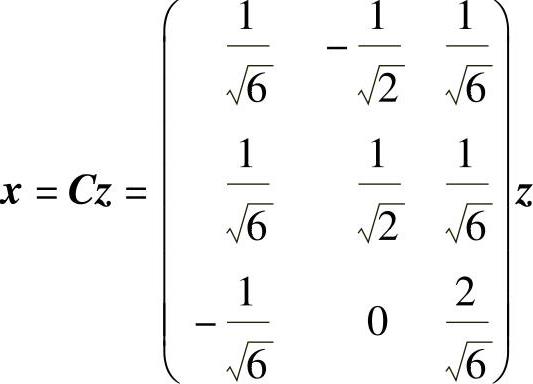
下化为规范形,即
f(x1,x2,x3)=z21-z22-z23.
附注 (Ⅰ)设A是n阶可逆矩阵,有特征值λ及对应的特征向量α,则A的伴随矩阵A∗有特征值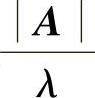 及对应的特征向量α.
及对应的特征向量α.
(Ⅱ)要熟练掌握用正交变换化二次型为标准形的方法.
(22)(Ⅰ)由于FZ(z)=P(Z≤z),其中
所以,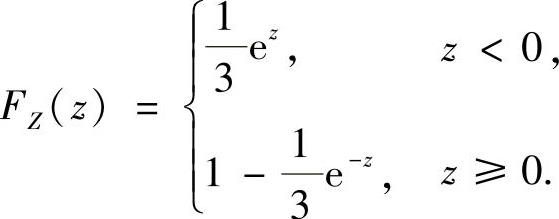
(Ⅱ)Cov(X,X2)=E(X3)-EX·E(X2),
其中,EX=1,E(X2)=D(X)+(EX)2=1+12=2,
所以,Cov(X,X2)=3E(X2)-E(X2)=2E(X2)=4.
附注 由于Z=XY是连续型随机变量与离散型随机变量之积,所以要计算它的分布函数应从定义出发,即从计算概率
P(Z≤z)=P(XY≤z)
入手.
(23)记X为独立重复射击中,直到命中时的射击次数,则k1,k2,…,kn为来自总体X的简单随机样本值.由于
P(X=k)=(1-p)k-1p(k=1,2,…),
所以,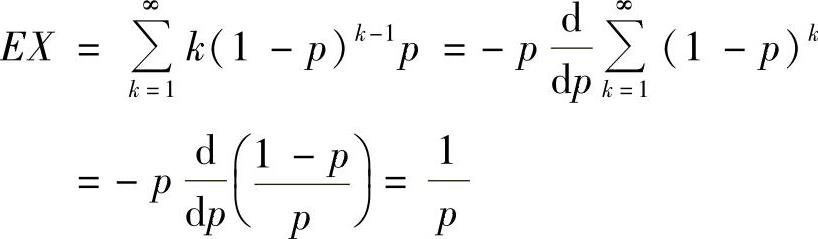
令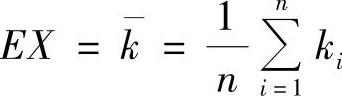 ,即
,即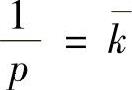 ,于是由矩估计法得p的矩估计值p
,于是由矩估计法得p的矩估计值p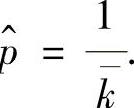
最大似然函数为
取对数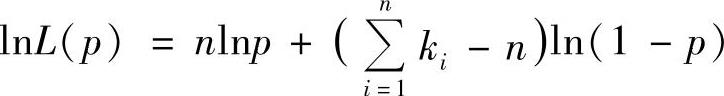 .令
.令
解此方程得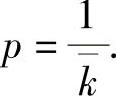 于是由最大似然估计法知p的最大似然估计值
于是由最大似然估计法知p的最大似然估计值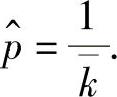
附注 应熟练掌握总体未知参数的两种点估法方法:矩估计法与最大似然估计法.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




