一、选择题
答案
(1)由于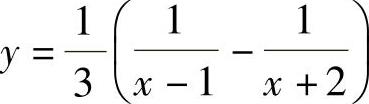 ,所以
,所以
所以选(B).
附注 要记住公式: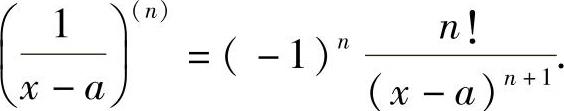
(2)由于利用对称区间上定积分的性质可得
所以 P<M<N.因此选(C).
附注 应记住对称区间上定积分的性质:设f(x)在[-a,a](a>0)上连续,则
此外,当f(x)是非奇非偶函数时有
(3)令x=et,则x2y″+xy′+y=2sinlnx成为
所以,原方程有形如y=t(acost+bsint)=(acoslnx+bsinlnx)lnx的特解.因此选(B).
附注 所给微分方程是2阶欧拉方程,令x=et可以转换成2阶常系数线性微分方程,由此即可确定应具有的特解形式.
(4)当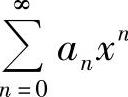 的收敛半径为1时,它在x=-1处可能条件收敛
的收敛半径为1时,它在x=-1处可能条件收敛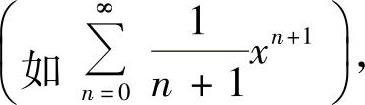 也可能不是条件收敛
也可能不是条件收敛
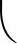 如
如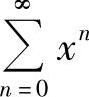 或
或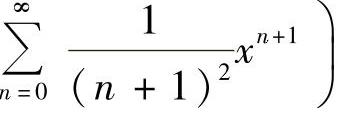 ,但当
,但当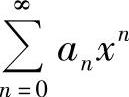 在点x=-1处条件收敛时,它的收敛半径必为1.于是收敛半径为1是
在点x=-1处条件收敛时,它的收敛半径必为1.于是收敛半径为1是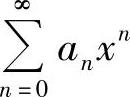 在点x=-1处条件收敛的必要而非充分条件.因此选(B).
在点x=-1处条件收敛的必要而非充分条件.因此选(B).
附注 对于幂级数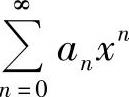 ,当其收敛半径为R(正数)时,
,当其收敛半径为R(正数)时,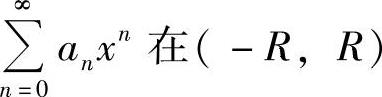 内绝对收敛,但在端点x=-R,R处可能收敛(条件收敛或绝对收敛),也可能发散,应视{an}而定.
内绝对收敛,但在端点x=-R,R处可能收敛(条件收敛或绝对收敛),也可能发散,应视{an}而定.
(5)由于B=P-1AP,所以当A有特征值λ及对应的特征向量为α时,B有特征值λ及对应的特征向量P-1α.因此由A可逆知B可逆,所以B∗有特征值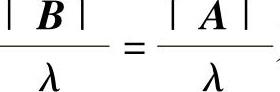 及对应的特征向量P-1α.因此选(C).
及对应的特征向量P-1α.因此选(C).
附注 应记住以下结论:
设A是n阶矩阵,有特征值λ及对应的特征向量α,则B=P-1AP(P是n阶可逆矩阵)有特征值λ和对应的特征向量P-1α;当A可逆时,A的伴随矩阵A∗有特征值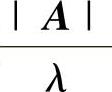 及对应的特征向量α.
及对应的特征向量α.
(6)由于当(Ⅰ)与(Ⅱ)等价时,(Ⅰ)与(Ⅱ)等秩;当A与B等价时,A与B等秩,反之也对,所以选项(A)、(C)、(D)都正确,因此选(B).
附注 当(Ⅰ)与(Ⅱ)等秩时,(Ⅰ)与(Ⅱ)未必等价.例如,α1=(1,0,0)T,α2=(0,1,0)T,β1=(1,0,0)T,β2=(0,0,1)T.显然r(α1,α2)=r(β1,β2),但是α2不能由β1,β2线性表示,即α1,α2与β1,β2不等价.
由本题可知:题中的(Ⅰ)、(Ⅱ)等价与A、B等价是有区别的,应注意这一点.
(7)记Ci={第i次取球取到的是白球}(i=1,2),则
所以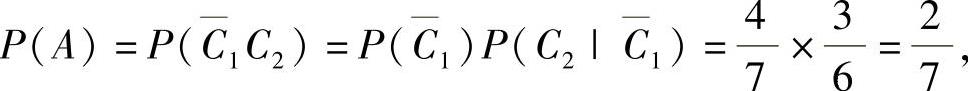
因此选(B).
附注 本题有两点值得注意:
(Ⅰ){第二次取球才取到白球}与{第二次取球取到的是白球}这两个随机事件是有区别的.
(Ⅱ)随机事件{第i次取球取到白球}(i=1,2,3)的概率是相等的,都为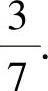
(8)由于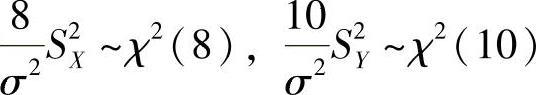 ,所以
,所以
且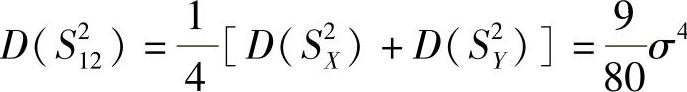 ,
,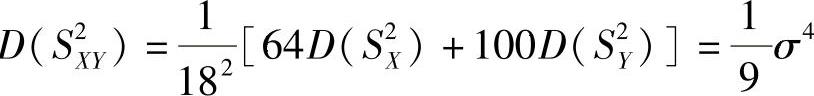 ,
,
所以,四个统计量中方差最小者为S2XY,因此选(D).
附注 记住以下结论:
设X1,X2,…,Xn是来自总体X~N(μ,σ2)的随机样本,记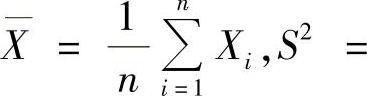
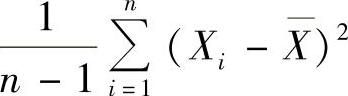 ,则
,则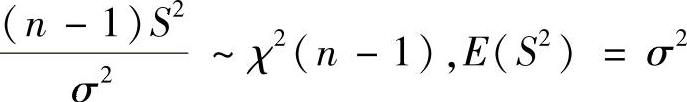 ,D
,D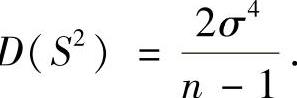
二、填空题
(9)由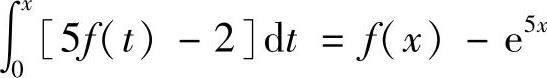 得
得
5f(x)-2=f′(x)-5e5x 以及f(0)=1,f′(0)=8,
所以有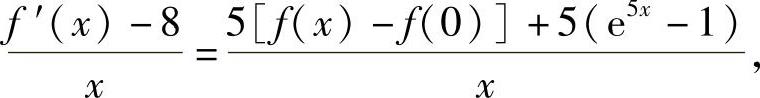
令x→0,由上式得
f″(0)=5f′(0)+5×5=65.
附注 本题也可以解答如下:由于对所给等式两边关于x求导得
5f(x)-2=f′(x)-5e5x,
上式对x求导得
5f′(x)=f″(x)-25e5x,即f″(x)=5f′(x)+25e5x.
于是利用f(0)=1,f′(0)=8得
f″(0)=5×8+25×1=65.
(10)显然x=0,y=0时,所给方程成为∫0zet2dt=0,从而z(0,0)=0.此外,所给方程两边对x求偏导数得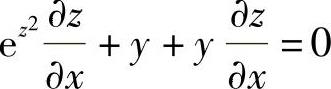 ,即
,即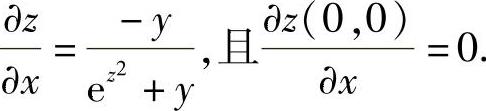
从而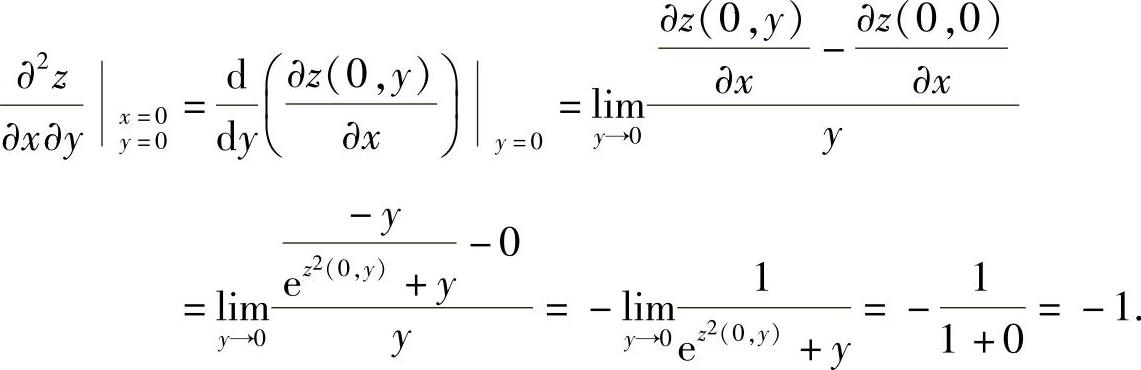
附注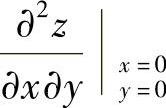 也可以由
也可以由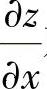 对y求偏导数算出
对y求偏导数算出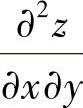 ,然后将x=y=z=0代入计算得到.但题解中由
,然后将x=y=z=0代入计算得到.但题解中由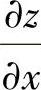 按定义计算
按定义计算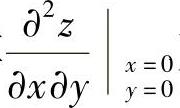 更加快捷些.
更加快捷些.
(11)设切点为M(x0,y0,z0),则S在点M处的法向量为(2x0-1,2y0,2z0),于是由切平面与π1与π2都垂直知
所以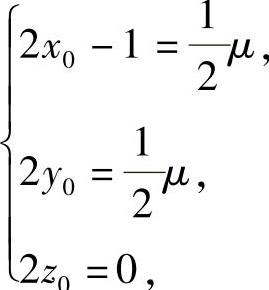 即
即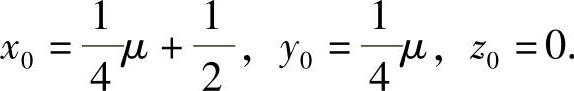
由M∈S知,x20+y20+z20=x0,即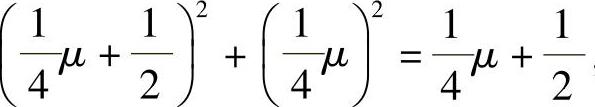 ,解此方程得
,解此方程得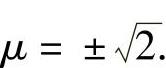
所以切点为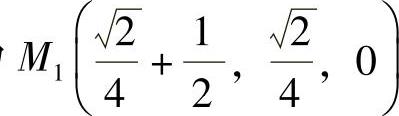 和
和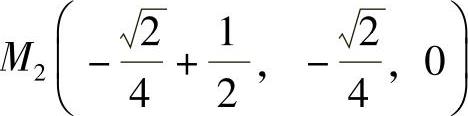 ,因此所求的切平面方程为
,因此所求的切平面方程为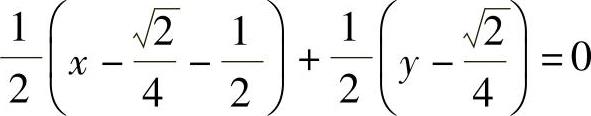 ,即
,即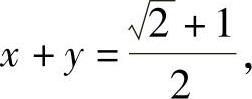
和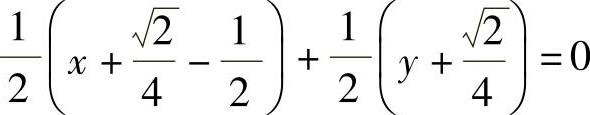 ,即
,即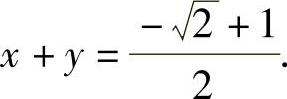
附注 计算曲面S的切平面时,如果未知切点坐标,总是根据有关条件先计算切点坐标,然后写出切平面方程.
(12)
附注 题解中有两点值得注意:
(Ⅰ)当曲线C是正向平面闭曲线时,曲线积分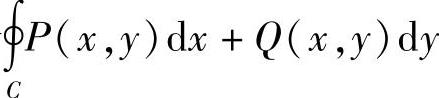 通常用格林公式计算比较快捷.
通常用格林公式计算比较快捷.
(Ⅱ)对于二重积分,应先利用积分区域的对称性化简以后再行计算,具体说,设D满足某种对称性,则二重积分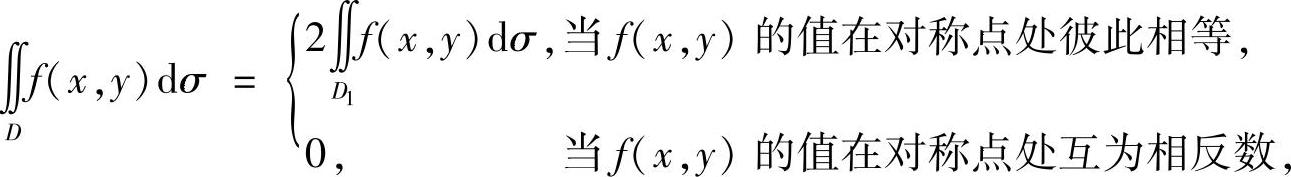 其中,D1是D按对称性划分成的两部分之一.
其中,D1是D按对称性划分成的两部分之一.
(13)显然|A|=2,此外
所以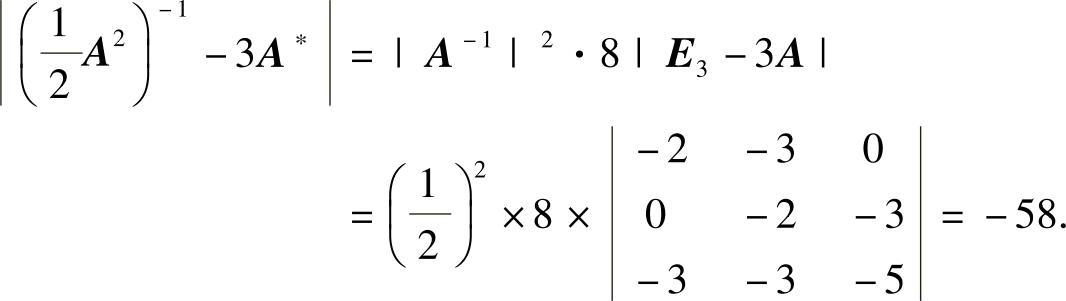
附注 计算矩阵的行列式时,以下结论是常用的:
设A,B都是n阶矩阵,则
|AB|=|A||B|,|kA|=kn|A|(k是常数),|A∗|=|A|n-1(n>1,A∗是A的伴随矩阵).
当A可逆时,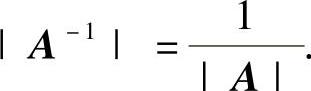
(14)由于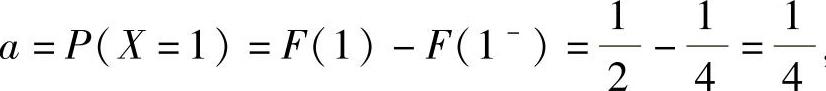 ,所以
,所以
附注 由于F(x)只有间断点x=0,1,2,所以X的分布列为
即
三、解答题
(15)D如图答8-15的阴影部分所示,所以
其中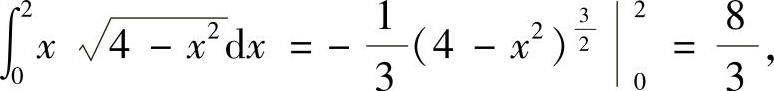
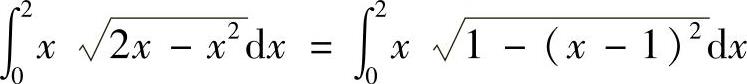
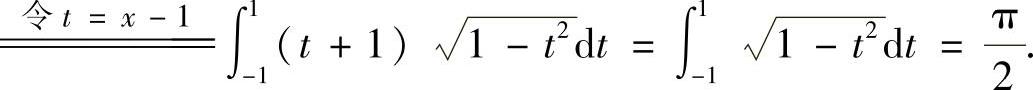
图答 8-15
所以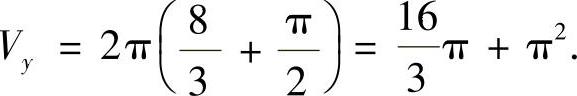
附注 应记住以下公式
设f1(x),f2(x)都是连续函数,且0≤f1(x)≤f2(x)(0≤a≤x≤b).
记D={(x,y)|0≤a≤x≤b,f1(x)≤y≤f2(x)},则D绕x轴旋转一周而成的旋转体体积
D绕y轴旋转一周而成的旋转体体积
(16)n=2时,由于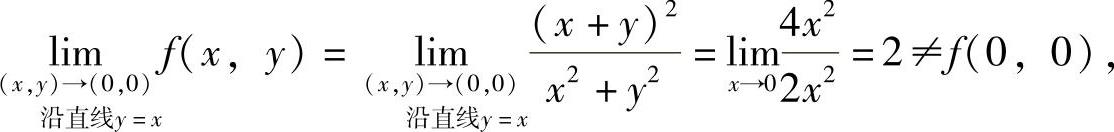
所以,此时f(x,y)在点(0,0)处不连续.(https://www.xing528.com)
n≥3时,由于当(x,y)→(0,0)时由
知,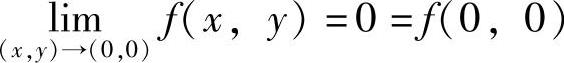 ,所以此时f(x,y)在点(0,0)处连续,因此使f(x,y)在点(0,0)处连续的最小n值为3.
,所以此时f(x,y)在点(0,0)处连续,因此使f(x,y)在点(0,0)处连续的最小n值为3.
所以,此时f(x,y)在点(0,0)处不可微.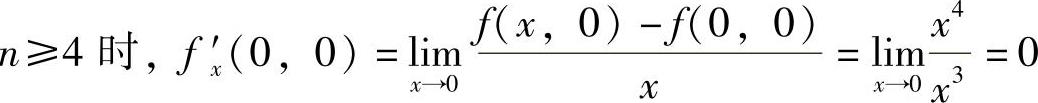 ,同样有f′y(0,0)=0.于是当(x,y)→(0,0)时由
,同样有f′y(0,0)=0.于是当(x,y)→(0,0)时由
知,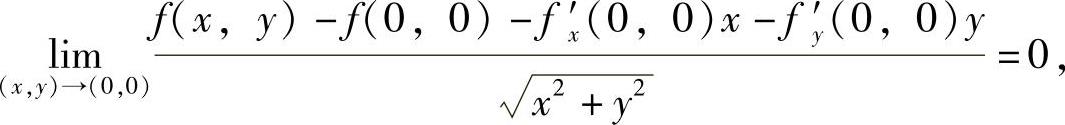
所以,此时f(x,y)在点(0,0)处可微.因此使f(x,y)在点(0,0)处可微的最小n值为4.
附注 本题的f(x,y)在点(0,0)处连续或可微都是由定义证明的.
设二元函数g(x,y)在点(x0,y0)处的某个邻域内有定义,如果
则f(x,y)在点(x0,y0)处可微.
(17)由题设知{xn}是正项数列,且对n=1,2,…有
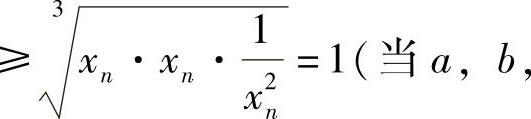 c都为非负数时,
c都为非负数时,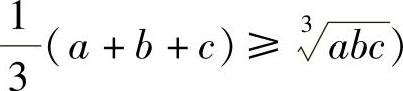
所以{xn}有下界.此时,由xn≥1(n=2,3,…)知
即{xn}单调不增.因此由数列极限存在准则Ⅱ知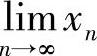 存在,记为A.对所给递推式两边令n→∞取极限得
存在,记为A.对所给递推式两边令n→∞取极限得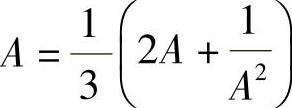 ,即A=1.
,即A=1.
由此得到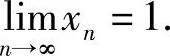
考虑极限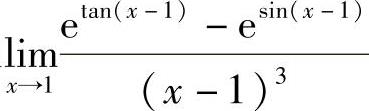 (即将欲求的极限式中的xn改为x,则当n→∞时,x→1):
(即将欲求的极限式中的xn改为x,则当n→∞时,x→1):
所以,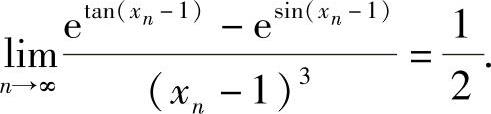
附注 数列极限有两个存在准则:
准则Ⅰ:设数列{xn},{yn}及{zn}满足
yn≤xn≤zn(n=1,2,…),
且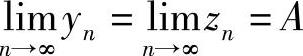 ,则
,则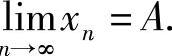
准则Ⅱ:设数列{xn}是由递推式x1,xn+1=f(xn)(n=1,2,…)确定.
如果{xn}单调不减有上界或单调不增有下界,则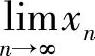 存在.
存在.
当数列{xn}由递推式确定时,通常总是利用数列极限存在准则Ⅱ,先确定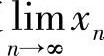 存在,然后对所给递推式两边令n→∞取极限算出极限值.
存在,然后对所给递推式两边令n→∞取极限算出极限值.
(18)记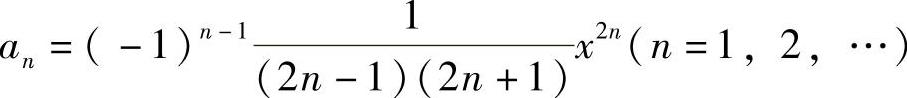 ,则
,则
且当x=-1,1时,所给幂级数都成为收敛级数
所以所给级数的收敛域为[-1,1].
对x∈[-1,0)∪(0,1]有
且当x=0时,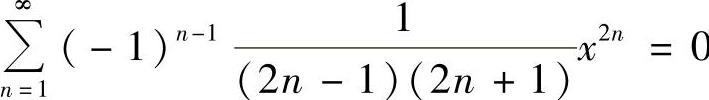 ,所以所给幂级数的和函数为
,所以所给幂级数的和函数为
附注 本题解答有两点值得注意:
(Ⅰ)所给幂级数是缺项幂级数,所以应将幂级数记为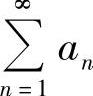 ,然后用比值法确定这个幂级数的收敛域.
,然后用比值法确定这个幂级数的收敛域.
(Ⅱ)x∈[-1,0)∪(0,1]时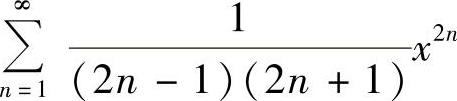 的和函数s(x)也可计算如下:
的和函数s(x)也可计算如下:
由于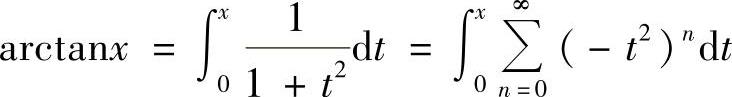
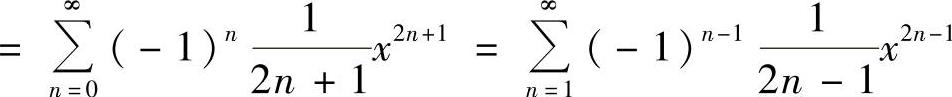 ,所以
,所以
(19)记S(不妨设其为外侧)围成的空间区域为Ω,则由高斯公式得
由于S是半空间x>0内任意有向闭曲面,所以由上式得
即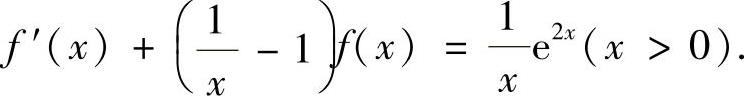
它的通解为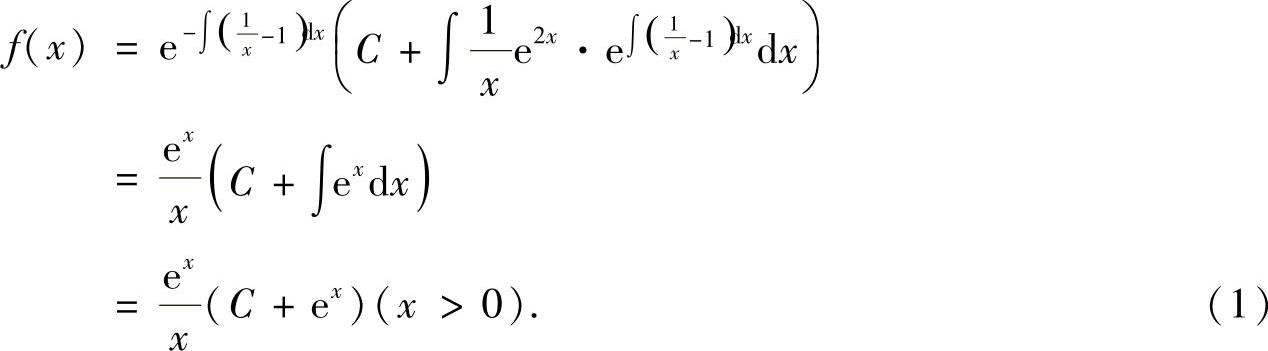
上式两边令x→0+取极限,且与题设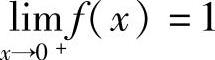 比较得
比较得
所以C=-1,将它代入式(1)得f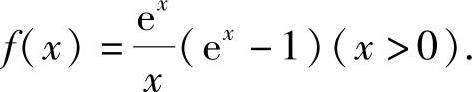
附注 闭曲面上的关于坐标的曲面积分通常用高斯公式计算比较快捷.高斯公式为:
设Σ是光滑或分块光滑有向闭曲面(外侧),它围成的空间闭区域为Ω,P(x,y,z),Q(x,y,z),R(x,y,z)都在Ω上具有连续偏导数,则
(20)由题设知(1,2,2,1)T-(1,-2,4,0)T=(0,4,-2,1)T是方程组Ax=0的解,所以有
4α2-2α3+α4=0,即α4=-4α2+2α3.
于是由A=(α1,α2,α3,α4)的秩为3知,α1,α2,α3线性无关.
此外,由题设(1,-2,4,0)T是方程组Ax=β的解得
β=α1-2α2+4α3,
于是方程组By=α1+2α2,即为
(α3,α2,α1,α1+2α2+2α3)y=α1+2α2. (1)
由于式(1)的系数矩阵的秩为3,且对应的齐次方程组有基础解系(2,2,1,-1)T.此外,式(1)有特解(0,2,1,0)T.所以方程组By=α1+2α2的通解为
y=C(2,2,1,-1)T+(0,2,1,0)T(其中,C是任意常数).
附注 要记住齐次线性方程组Ax=0(其中,A是m×n矩阵,x是n维未知列向量)的基础解系中所包含的线性无关解向量个数为n-r(A).
(21)(Ⅰ)由于
所以f(x1,x2,x2)的矩阵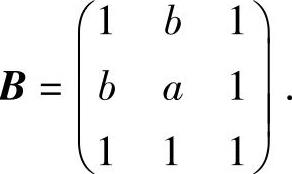
由于B有特征值为λ=0,1,4,所以有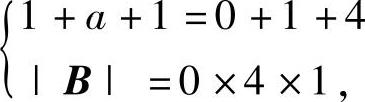 ,即a=3,b=1.
,即a=3,b=1.
(Ⅱ)由以上计算知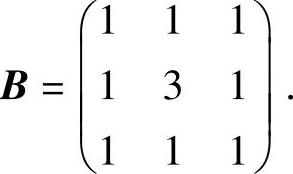
设B对应λ=0的特征向量为α=(a1,a2,a3),则α满足
由于
所以式(1)与方程组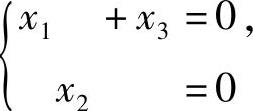 同解,可取它的基础解系为α,即α=(1,0,-1)T.
同解,可取它的基础解系为α,即α=(1,0,-1)T.
设B对应λ=1的特征向量为β=(b1,b2,b3)T,则β满足
由于
所以式(2)与方程组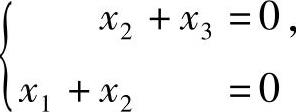 同解,可取它的基础解系为β,即β=(-1,1,-1)T.
同解,可取它的基础解系为β,即β=(-1,1,-1)T.
设B对应λ=4的特征向量为γ=(c1,c2,c3)T,则由B是实对称矩阵知γ与α,β都正交,于是有
可取它的基础解系为γ,即γ=(1,2,1)T.显然α,β,γ两两正交,现将它们单位化:
记Q=(ξ1,ξ2,ξ3)(正交矩阵),则x=Qy,即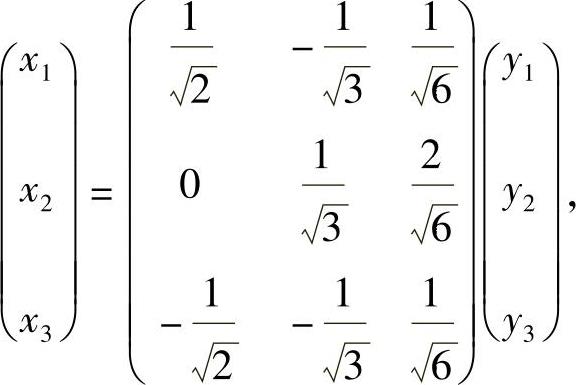
使得 f(x1,x2,x3)=y22+4y23(标准形).
附注 题中的A不是实对称矩阵,所以要用正交变换将f(x1,x2,x3)=xTAx化为标准形,必须首先将f(x1,x2,x3)改写成xTBx(其中,B是实对称矩阵).此外,要熟练掌握,用正交变换把二次型化成标准形的方法.
(22)(Ⅰ)由于当y>0时,
所以,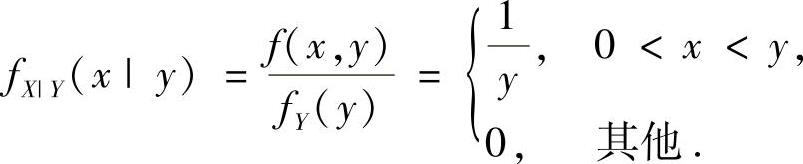
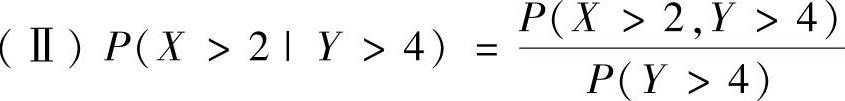 ,其中,
,其中,
附注 对于二维连续型随机变量(X,Y),必须掌握其两种条件概率P(X≥a|Y≥b)和P(X≥a|Y=b)的计算方法.
(23)(Ⅰ)由于EX=0·θ2+1·2θ(1-θ)+2·θ2+3·(1-2θ)=3-4θ.
样本值的平均值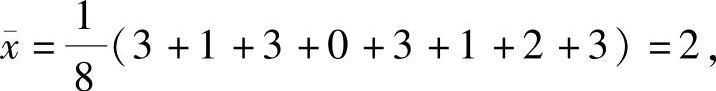
所以由矩估计法,令EX=x¯,即3-4θ=2得θ的矩估计值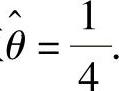
(Ⅱ)由题设知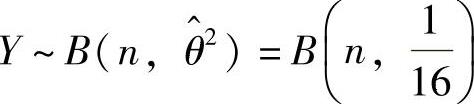 ,所以对于任意实数y,由中心极限定理(具体是棣莫弗-拉普拉斯定理)得
,所以对于任意实数y,由中心极限定理(具体是棣莫弗-拉普拉斯定理)得
因此,所求的参数为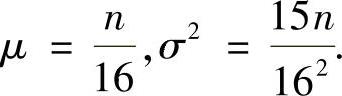
附注 计算关于随机变量X~N(μ,σ2)的概率问题时,总是引入标准化随机变量X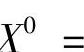
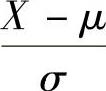 ,则X0~N(0,1)(标准正态分布),于是X的分布函数
,则X0~N(0,1)(标准正态分布),于是X的分布函数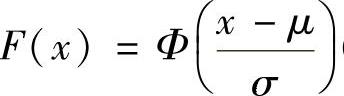 (其中,Φ(u)是标准正态分布函数),即
(其中,Φ(u)是标准正态分布函数),即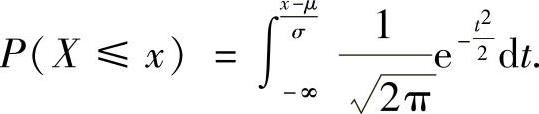
由此可知,当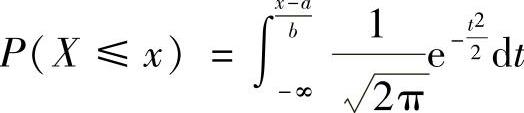 时,X~N(a,b2).本题中的参数就是如此得到的.
时,X~N(a,b2).本题中的参数就是如此得到的.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




