一、选择题
答案
(1)显然x=0,1都是方程的实根.记f(x)=2x-x2-1,则f(x)连续,且
所以由零点定理推广形式知所给方程f(x)=0在(2,+∞)上有实根,记为x0.
如果方程f(x)=0还有不同实根x1,不妨x1>x0,则由f(x)可导,且f(0)=f(1)=f(x0)=f(x1)及罗尔定理(高阶导数形式)知,存在ξ∈(0,x1),使得f‴(ξ)=0.(1)
另一方面,计算f(x)的3阶导数得f‴(ξ)=2ξ(ln2)3≠0.(2)
式(1)与式(2)矛盾知,方程2x-x2-1=0除实根0,1,x0外别无其他实根,因此选(C).
附注 (Ⅰ)零点定理的一种推广形式
设函数f(x)在[a,+∞)上连续,且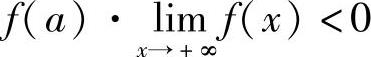 ,则存在ξ∈(a,+∞),使得f(ξ)=0.
,则存在ξ∈(a,+∞),使得f(ξ)=0.
(Ⅱ)罗尔定理的高阶导数形式
设函数f(x)在(a,b)内2阶可导,且有x1,x2,x3∈(a,b)(其中,x1<x2<x3),使得f(x1)=f(x2)=f(x3),则存在ξ∈(a,b),使得f″(ξ)=0.
设函数f(x)在(a,b)内3阶可导,且有x1,x2,x3,x4∈(a,b)(其中,x1<x2<x3<x4),使得f(x1)=f(x2)=f(x3)=f(x4),则存在ξ∈(a,b),使得f‴(ξ)=0.
(2)由于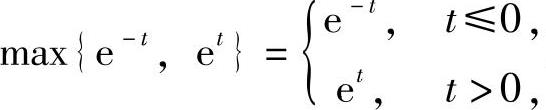 所以
所以
因此选(A).
附注 同样可以计算∫-x∞min{e-t,et}dt,具体如下:
由于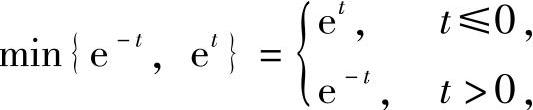 所以
所以
(3)由{an}是单调减少收敛于零的正项数列知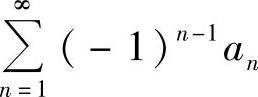 收敛.所以对它两项两项地加括号所得级数
收敛.所以对它两项两项地加括号所得级数
收敛.因此选(D).
附注 本题获解的关键是,由莱布尼茨定理确定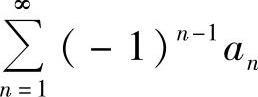 收敛.此外,应记住以下的收敛级数性质:
收敛.此外,应记住以下的收敛级数性质:
设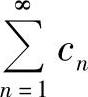 收敛,则对它任意加括号所得级数仍收敛,但反之未必正确,即级数
收敛,则对它任意加括号所得级数仍收敛,但反之未必正确,即级数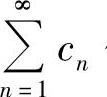 任意加括号后所得的级数收敛时,原级数未必收敛.
任意加括号后所得的级数收敛时,原级数未必收敛.
(4)由于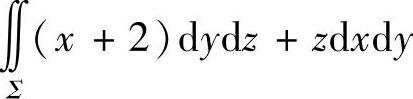
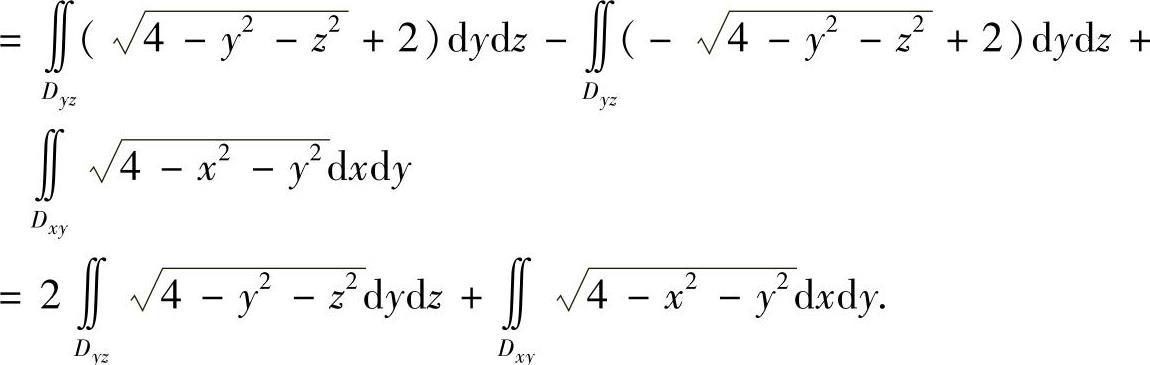
所以选(C).
附注 题中计算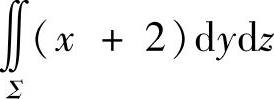 时,需用平面x=0将Σ划分成两部分:
时,需用平面x=0将Σ划分成两部分: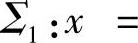
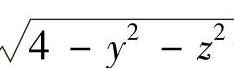 (前侧)与
(前侧)与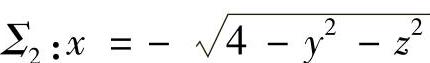 (后侧),它们在yOz平面的投影都为Dyz.
(后侧),它们在yOz平面的投影都为Dyz.
(5)由α,β,γ线性无关知α,β线性无关,从而由α,β,δ线性相关知δ可由α,β线表示,即δ可由α,β,γ线性表示.因此选(B).
附注 关于向量组的线性相关性的以下结论应记住:
(Ⅰ)设向量组(A):α1,α2,…,αm.
如果(A)线性无关,则它的任一部分组也线性无关;
如果(A)的某一部分组线性相关,则(A)线性相关.
(Ⅱ)设向量组(A):α1,α2,…,αm,β.
如果(A)线性相关,则至少存在一个向量可用其余向量线性表示;
如果(A)线性相关,但α1,α2,…,αm线性无关,则β可由α1,α2,…,αn线性表示,且表示式是唯一的.
(6)②④都是A可相似对角化的充分必要条件,因此选(C).
附注 应记住以下的结论:
设A是n阶矩阵,则“A有n个线性无关的特征向量”,或“A的每个ni重特征值λi的特征矩阵λiEn-A都满足r(λiE-A)=n-ni”,都是A可相似对角化的充分必要条件.而A有n个不同的特征值,或A是实对称矩阵,则是A可相似对角化的充分而非必要条件.
(7)对于选项(C),(X,Y)的概率密度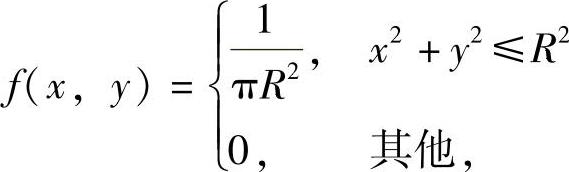 ,它的关于X与Y的边缘概率密度分别为
,它的关于X与Y的边缘概率密度分别为
显然fX(x)fY(y)=f(x,y)不是几乎处处成立的,所以X与Y不相互独立.因此选(C).
附注 应记住选项(A),(B),(D)的结论.
(8)由于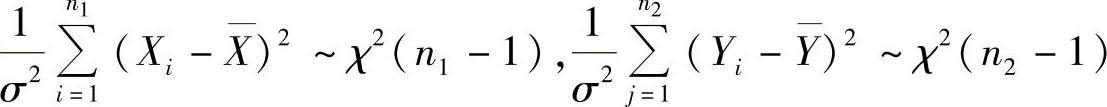 ,且
,且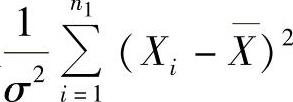
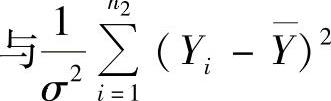 相互独立,所以由χ2分布的可加性得
相互独立,所以由χ2分布的可加性得
于是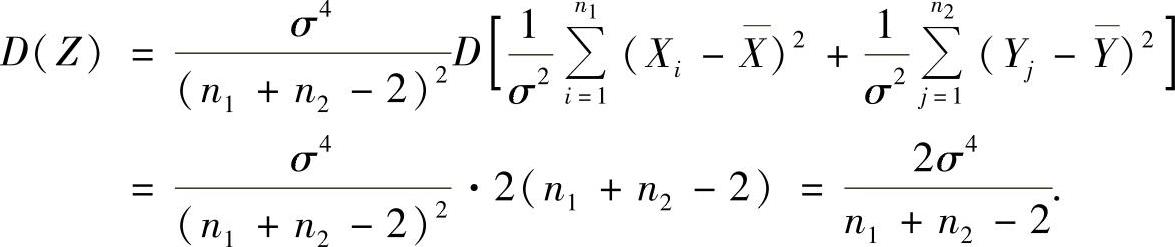
因此选(D).
附注 要记住以下的关于χ2分布的结论:
(Ⅰ)设X~χ2(n),则EX=n,DX=2n;
(Ⅱ)设X~χ2(n1),Y~χ2(n2)且它们相互独立,则X+Y~χ2(n1+n2).
二、填空题
(9)由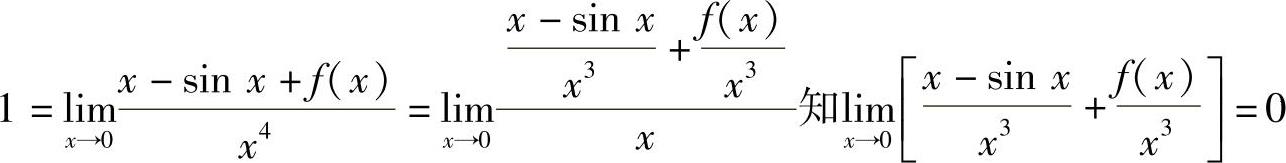 ,从而
,从而
附注 类似地可考虑:
设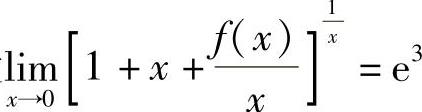 ,求
,求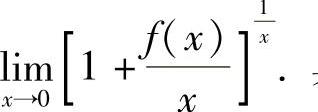 具体计算如下:
具体计算如下:
由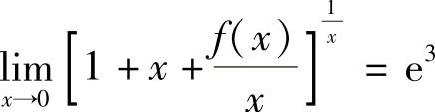 得
得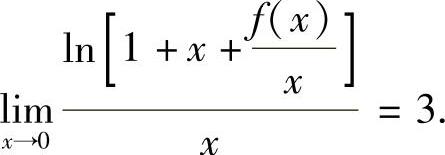 由此可得
由此可得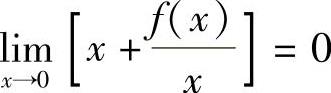 ,即
,即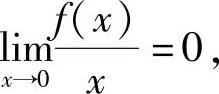 以及
以及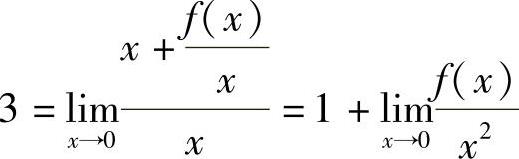 ,即
,即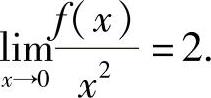
所以,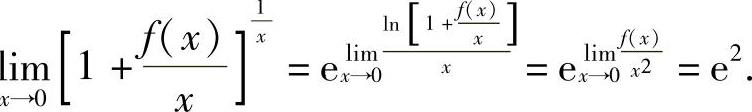
(10)由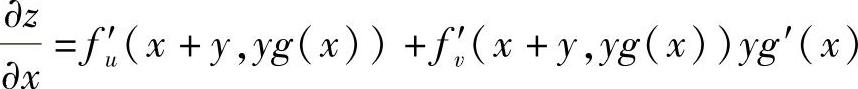 得
得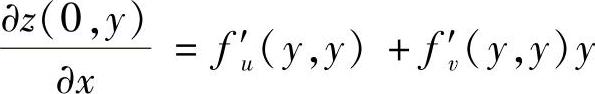 (利用g(0)=g′(0)=1)
(利用g(0)=g′(0)=1)
=f′x(y,y)+f′y(y,y)y=1+y(利用f′x(y,y)=f′y(y,y)=1),
所以,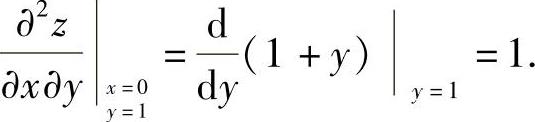
附注 由于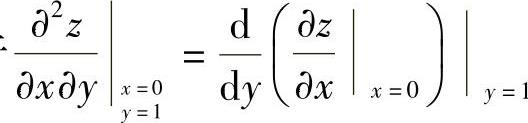 ,所以可先算出
,所以可先算出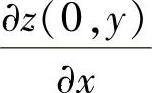 ,记为φ(y),然后计算
,记为φ(y),然后计算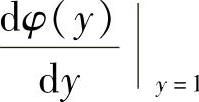 即得
即得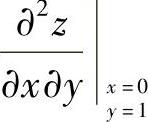 ,这样计算比先算出
,这样计算比先算出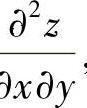 ,然后将x=0,y=1代入计算
,然后将x=0,y=1代入计算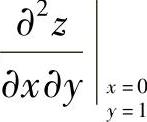 快捷.
快捷.
(11)由于曲面z=x2+y2与x2+y2+z2=2(z≥0)的交线为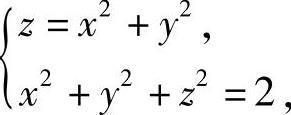 即
即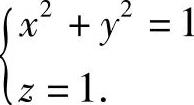 ,所以Σ在xOy平面的投影为D={(x,y)|x2+y2≤1},从而Σ的面积
,所以Σ在xOy平面的投影为D={(x,y)|x2+y2≤1},从而Σ的面积
附注 顺便计算上半球面x2+y2+z2=2(z≥0)位于曲面z=x2+y2之内部分Σ1的面积S1:
(12)将f(x)偶延拓为周期是2的周期函数f1(x),其中在[-1,1]上
所以,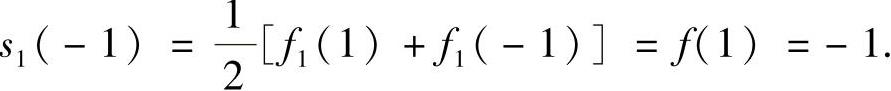
将f(x)奇延拓为周期为2的周期函数f2(x),其中在(-1,1]上
所以
附注 应记住:要计算f(x)(0≤x≤l)的余弦级数(正弦级数)时,应将f(x)作偶延拓(奇延拓).此外应掌握用狄利克雷收敛定理计算傅里叶级数的和函数的方法.
(13)由于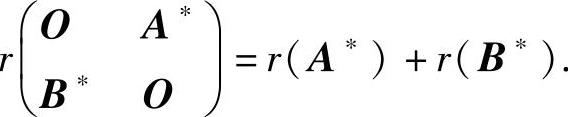 其中,A是2阶矩阵,所以当r(A)=1时,r(A∗)=1;B是4阶矩阵,所以当r(B)=2时,r(B∗)=0.
其中,A是2阶矩阵,所以当r(A)=1时,r(A∗)=1;B是4阶矩阵,所以当r(B)=2时,r(B∗)=0.
从而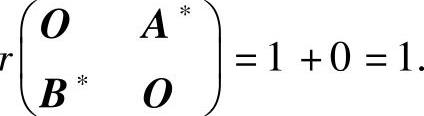
附注 应记住以下公式:
设A是n阶矩阵,A∗是A的伴随矩阵,则
(14)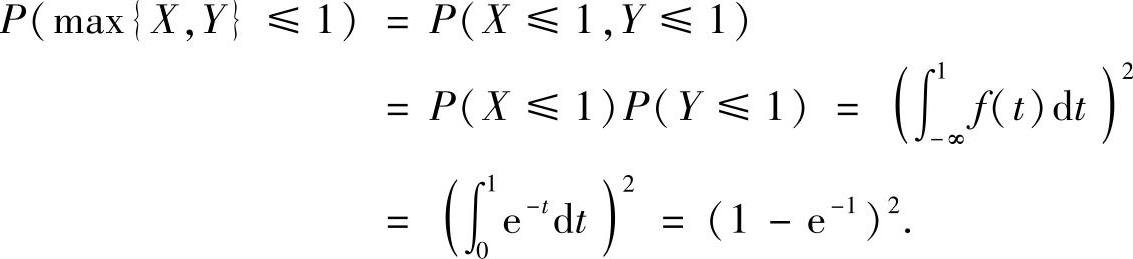
附注 应记住以下公式:
设随机变量X,Y相互独立,它们的分布函数分别为FX(x)与FY(y),则Z1=max{X,Y}的分布函数FZ1(z)=FX(z)FY(z);
Z2=min{X,Y}的分布函数FZ2(z)=1-[1-FX(z)][1-FY(z)].
三、解答题
(15)y(0)=1,此外,
由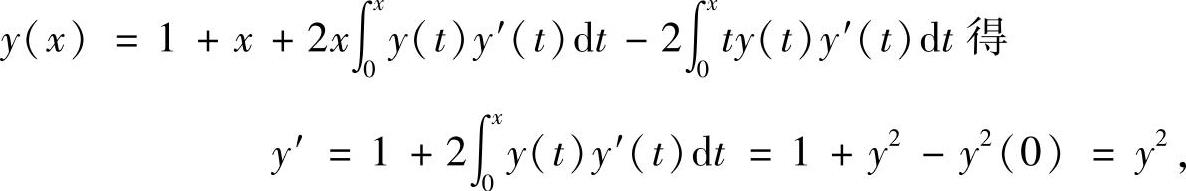
所以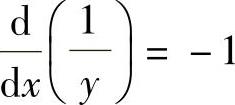 ,从而
,从而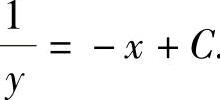 将y(0)=1代入得C=1.因此y
将y(0)=1代入得C=1.因此y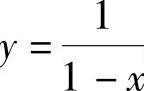 .从而
.从而
附注 对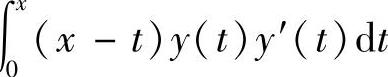 求导时,必须首先将被积函数中的x提到积分号之外,故将它改写成
求导时,必须首先将被积函数中的x提到积分号之外,故将它改写成
(16)由于f′x=2(x+1),f′y=2(y+1),f′z=-2z,所以由方程组
在Ω内部无解知,f(x,y,z)在Ω内部无可能极值点.
下面计算f(x,y,z)在Ω的表面上的最值.(https://www.xing528.com)
记F(x,y,z)=2x+2y+x2+y2-z2+λ(x2+y2+z2-1),则
F′x=2(1+x+λx),F′y=2(1+y+λy),F′z=2(-1+λ)z.
于是方程组
由式(1)与式(2)知x=y,由式(3)知z=0或λ=1.
将x=y,z=0代入式(4)得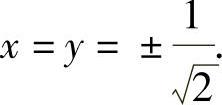 这时可能极值点为
这时可能极值点为
将x=y,λ=1代入式(1)、式(2)得x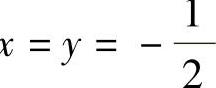 ,将它们代入式(4)得
,将它们代入式(4)得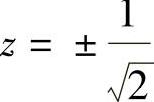 .这时可能极值点为
.这时可能极值点为
由于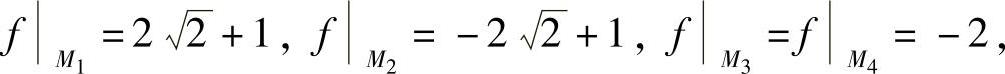 所以f(x,y,z)在Ω上的最大值为
所以f(x,y,z)在Ω上的最大值为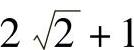 ,最小值为-2.
,最小值为-2.
附注 计算三元函数f(x,y,z)在有界闭区域Ω上的最值,通常可按以下步骤进行:
(Ⅰ)计算f(x,y,z)在Ω内部的所有可能极值点,记为M1,M2,…,Mn.
(Ⅱ)计算f(x,y,z)在Ω的边界上的最值(通常使用拉格朗日乘数法),记最大值为M,最小值为m.
(Ⅲ)比较f(M1),f(M2),…,f(Mn),M,m的大小,则最大者与最小者,分别为f(x,y,z)在Ω上的最大值与最小值.
(17)记f(x)=2sinx+tanx-3x,则
即 f(x)在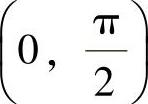 内单调增加.所以,对
内单调增加.所以,对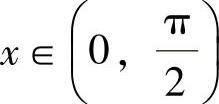 ,有
,有
附注 要证明函数不等式f(x)>g(x)(x∈(a,b))(其中,f(x)与g(x)在(a,b)内可导),总是按以下步骤进行:
(Ⅰ)作辅助函数φ(x)=f(x)-g(x);
(Ⅱ)计算φ′(x).
如果 φ′(x)>0(x∈(a,b)),且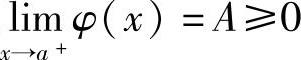 ,则有
,则有
φ(x)>0,即f(x)>g(x)(x∈(a,b)).
如果φ′(x)<0(x∈(a,b)),且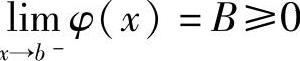 ,则有
,则有
φ(x)>0,即f(x)>g(x)(x∈(a,b)).
如果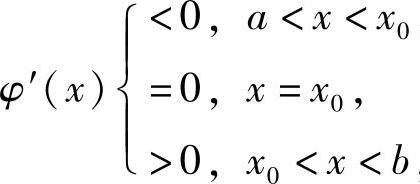 且φ(x0)=C>0,则有
且φ(x0)=C>0,则有
φ(x)>0,即f(x)>g(x)(x∈(a,b)).
(18)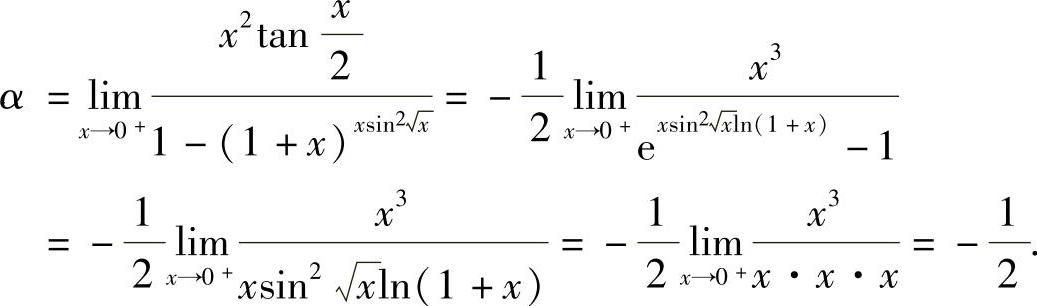
由于当x<1时有
所以,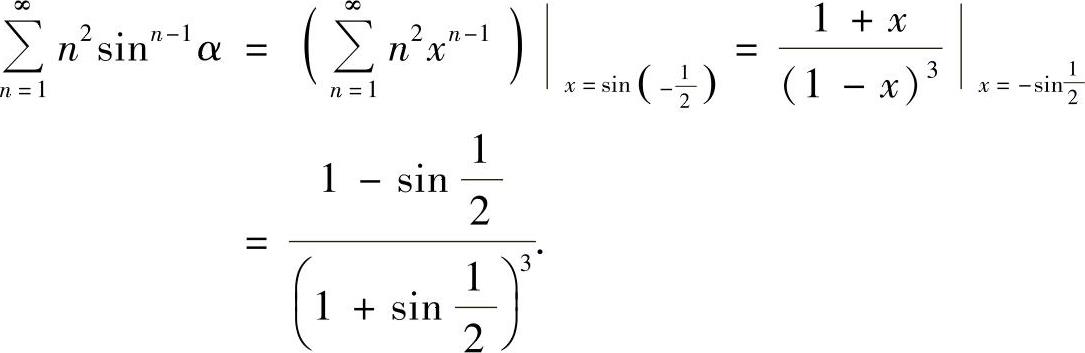
附注 利用幂级数计算级数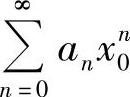 和的步骤如下
和的步骤如下
(Ⅰ)构造幂级数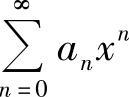 ,
,
(Ⅱ)计算上述幂级数的收敛域I与和函数s(x),
(Ⅲ)如果x0∈I,则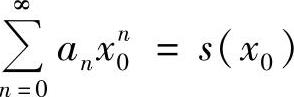 ,
,
本题就是如此计算的.
图答 7-19
(19)C如图答7-19所示的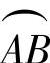 ,其中,A=(-aπ,0),B=(aπ,0).
,其中,A=(-aπ,0),B=(aπ,0).
作正向闭曲线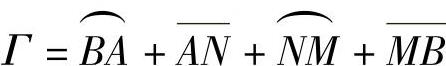 ,其中,
,其中,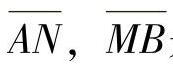 是位于x轴上的线段,
是位于x轴上的线段, 是上半圆x2+y2=ε2(y≥0),ε是充分小的正数,使得
是上半圆x2+y2=ε2(y≥0),ε是充分小的正数,使得 位于
位于 下方.记上述闭曲线围成的区域为D,则由格林公式得
下方.记上述闭曲线围成的区域为D,则由格林公式得
附注 由于C不是闭曲线,不能直接应用格林公式计算所给的曲线积分,所以要添上一段曲线C1,使之成为正向闭曲线Γ,这里对C1有以下要求:
(Ⅰ)要求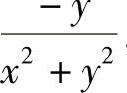 ,
,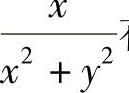 在Γ围成的闭区域上具有连续的偏导数;
在Γ围成的闭区域上具有连续的偏导数;
(Ⅱ)要求在C1上的曲线积分比较容易计算.题中所取的C1(即 )就是按此要求确定的.
)就是按此要求确定的.
(20)(Ⅰ)方程组(A)的增广矩阵
所以,线性方程(A)有无穷多解时,有a+1=0,即a=-1.
(Ⅱ)当a=-1时,方程组(A)与(B)组成的方程组为
对(C)的增广矩阵施行初等行变换:
由此可知,有公共解时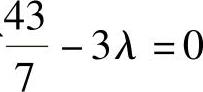 ,即
,即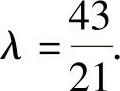 公共解为
公共解为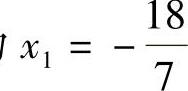 ,x2=3,
,x2=3,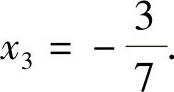
附注 设方程组A1x=b1,A2x=b2(其中A1,A2分别是m1×n与m2×n矩阵,b1,b2分别是m1维与m2维列向量,则这两个方程组有公共解的充分必要条件为方程组`
有解.
(21)(Ⅰ)由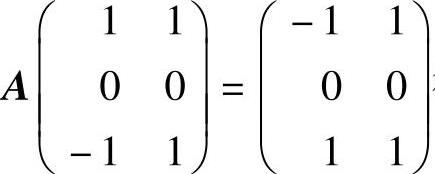 得
得
所以,矩阵A有特征值λ=-1,1.由r(A)=2知A还有特征值λ=0.显然对应λ=-1,1分别有特征向量α1=(1,0,-1)T和α2=(1,0,1)T.设对应λ=0的特征向量为α3=(x1,x2,x3)T,则由A是实对称矩阵知α3与α1,α2都正交,故有
所以可取它的基础解系为α3,即α3=(0,1,0)T.显然α1,α2,α3是正交向量组,现将它们单位化得
记Q=(ξ1,ξ2,ξ3)(正交矩阵),则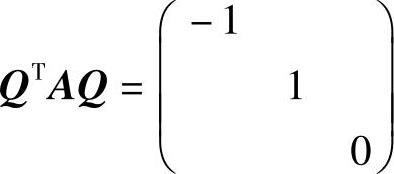 .于是
.于是
从而按伴随矩阵的定义得A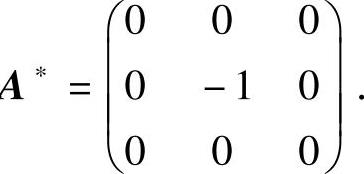
(Ⅱ)显然|Q|=-1,所以Q∗=|Q|Q-1=-QT,因此
QTA∗Q=-Q∗A∗(-QT)∗=(QTAQ)∗.于是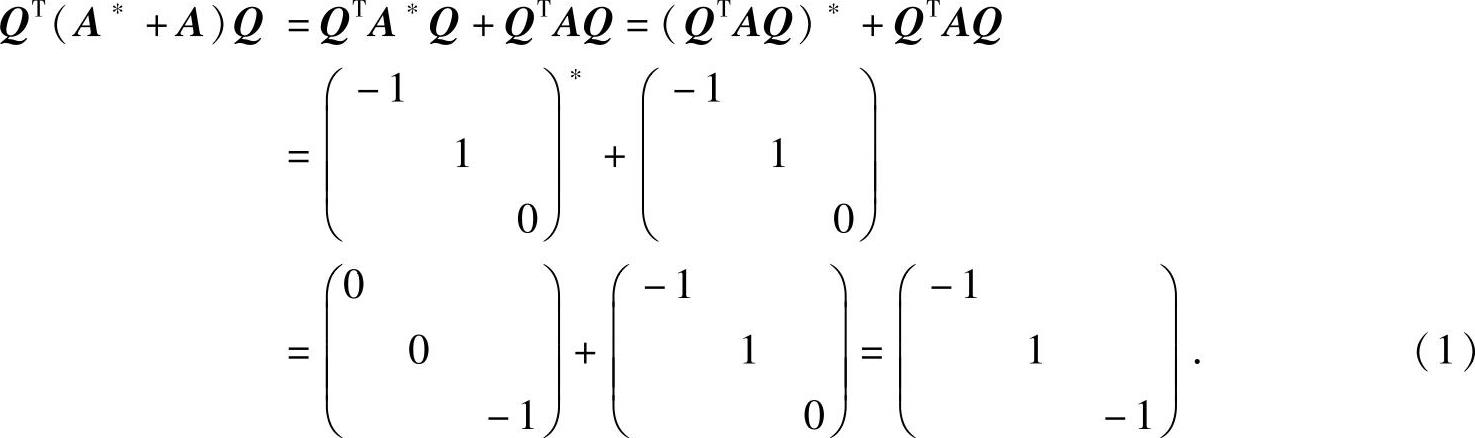
由此可知,取C=Q,则在正交变换x=Cy=Qy下,二次型f(x1,x2,x3)化为标准形y21+y22-y23.
附注 我们知道,使xTAx化为标准形的正交变换也使xTA∗x化为标准形,即xTA∗x=μ1y21+μ2y22+μ3y23,其中μ1,μ2,μ3是A∗的特征值.当|A|≠0时,μ1,μ2,μ3可由A的特征值λ1,λ2,λ3直接得到,即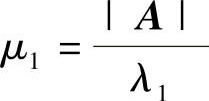 ,
,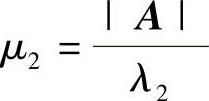 ,
,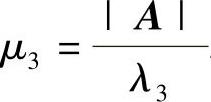 .但是现在|A|=0,故为了算出μ1,μ2,μ3,或为了将xT(A∗+A)x化为标准形,采用了题解中的方法.
.但是现在|A|=0,故为了算出μ1,μ2,μ3,或为了将xT(A∗+A)x化为标准形,采用了题解中的方法.
(22)(Ⅰ)由于(U,V)关于U的边缘概率密度为
所以,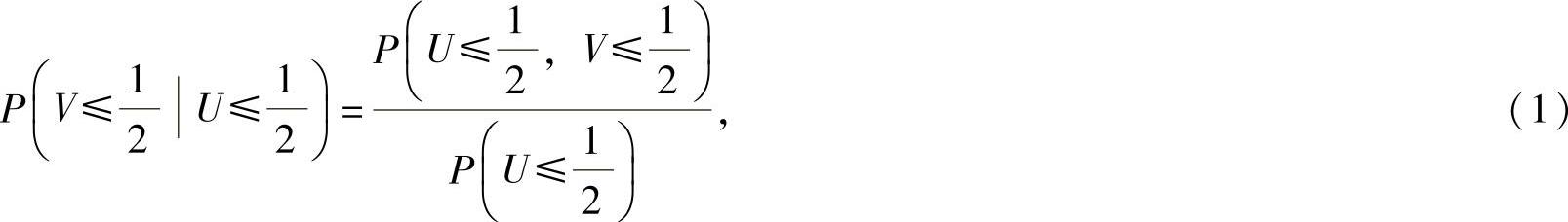
其中,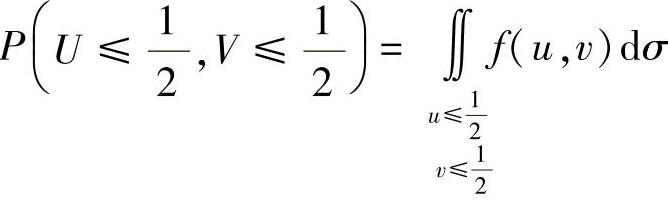
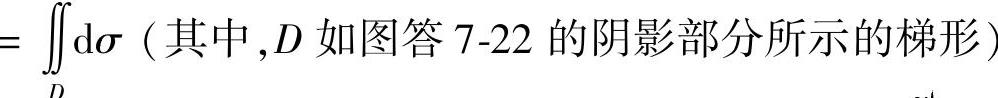
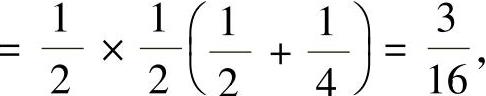
图答 7-22
因此,由式(1)得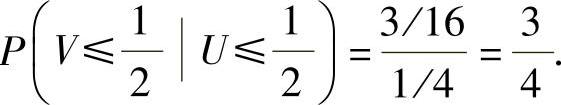
于是P(X=-1,Y=1)=P(X=1,Y=-1)=P(X=0,Y=1)=0.25.
记(X,Y)的概率分布为
则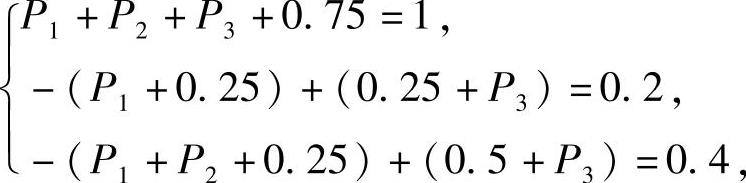 即
即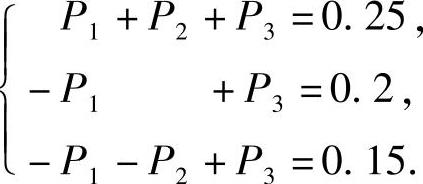
所以P1=0,P2=0.05,P3=0.2.因此(X,Y)的概率分布为
(Ⅱ)Cov(X,Y)=E(XY)-EX·EY,
其中E(XY)=(-1)×(-1)×0+(-1)×1×0.25+0×(-1)×0.05+0×1×0.25+
1×(-1)×0.25+1×1×0.2=-0.3,
所以,Cov(X,Y)=-0.3-0.2×0.4=-0.38.
附注 本题是连续型随机变量与离散型随机变量结合的综合题,需计算许多元素,因此对题目审视后应确定计算各个元素的先后顺序:
先计算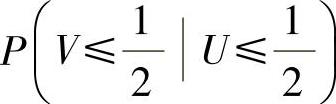 ,为此需先算出关于U的边缘概率密度fU(u);
,为此需先算出关于U的边缘概率密度fU(u);
然后确定(X,Y)的概率分布表,将已知的概率填入,对于未知的概率用P1,P2,P3等表示,并利用已知条件逐一确定这些未知的概率.
最后根据(X,Y)的概率分布算出Cov(X,Y).
(23)(Ⅰ)由于关于X的边缘概率密度为
其中,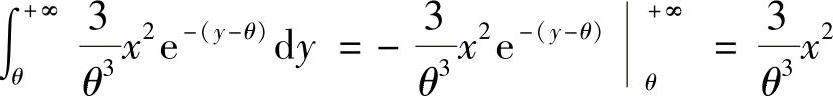 ,所以
,所以
由于E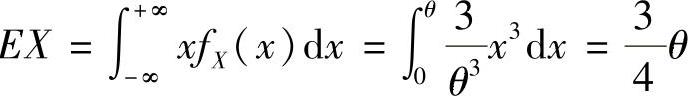 ,所以由矩估计法,令
,所以由矩估计法,令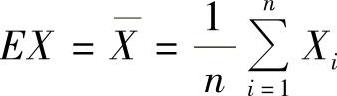 ,即
,即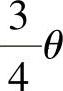
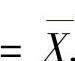 由此得到θ的矩估计量为
由此得到θ的矩估计量为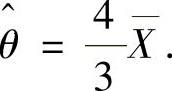
由于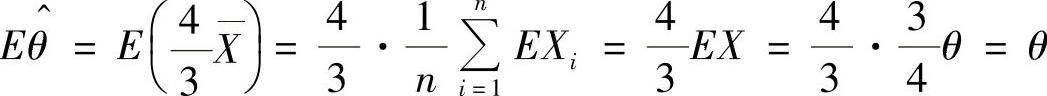 ,所以
,所以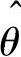 是无偏估计量.
是无偏估计量.
其中,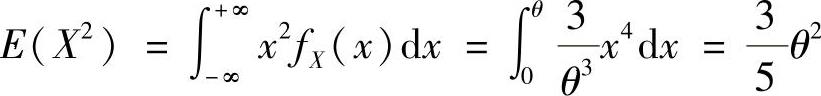 .所以
.所以
附注 要熟练掌握总体未知参数的两种点估计方法:矩估计法与最大似然估计法.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




