一、选择题
答案
(1)f(x)=x|x|·(x-2)2|x-2|,可能不可导点为x=0,2.在点x=0附近,
且由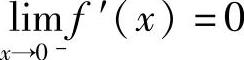 ,
,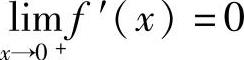 知f′(0)=0.
知f′(0)=0.
所以,x=0是f(x)的2阶不可导点.
在点x=2附近,
且由lim ,
, 知f′(2)=0.
知f′(2)=0.
所以,x=2是f(x)的2阶可导点.因此选(B).
附注 如果记住以下结论,本题将快捷获解:
(Ⅰ)(x-a)|x-a|在点x=a处2阶不可导,(x-a)2|x-a|在点x=a处2阶可导;
(Ⅱ)设f(x)=φ(x)g(x),其中φ(x)在点x=a处可导而2阶不可导,g(x)在点x=a处2阶可导且g(a)≠0,则f(x)在点x=a处2阶不可导.
(2)由于x2在[0,1]上连续,选项(A),(B),(C)右边都是x2在[0,1]上的积分和式的极限,它们都等于 ,即选项(A),(B),(C)都正确.因此选(D).
,即选项(A),(B),(C)都正确.因此选(D).
附注 也可以通过直接计算,确认选项(D)不正确:
(3)由于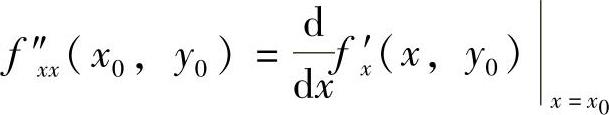 ,所以由f″xx(x,y)在点(x0,y0)处存在知f′x(x,y0)在点x0处可微.因此选(D).
,所以由f″xx(x,y)在点(x0,y0)处存在知f′x(x,y0)在点x0处可微.因此选(D).
附注 当题中所给的三个2阶偏导数在点(x0,y0)处连续时,选项(A),(B),(C)都正确,但仅假定这三个2阶偏导数在点(x0,y0)处存在时,未必能推出这三个选项都正确.
(4)由于Ω关于平面π:x+y+z=0对称,设M1(x1,y1,z1)与M2(x2,y2,z2)为对称点,则线段M1M2的中点 位于平面π上,所以
位于平面π上,所以 ,即x1+y1+z1=-(x2+y2+z2).
,即x1+y1+z1=-(x2+y2+z2).
从而tan(x1+y1+z1)=-tan(x2+y2+z2),即tan(x+y+z)在对称点处的值互为相反数,于是有
因此选(B).
附注 计算三重积分时,应先按积分区域的对称性进行化简,然后计算.对于三重积分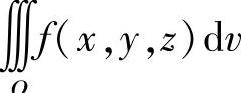 ,如果Ω具有某种对称性,且按此对称性Ω被划分成Ω1与Ω2两部分,则Ω
,如果Ω具有某种对称性,且按此对称性Ω被划分成Ω1与Ω2两部分,则Ω
当f(x,y,z)在对称点处的值互为相反数时,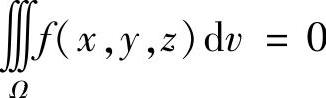 ;当f(x,y,z)在对称点处的值彼此相等时,
;当f(x,y,z)在对称点处的值彼此相等时,
(5)由于方程组Ax=0的解x0可使ATAx0=0,即x0也是方程组ATAx=0的解.反之,设ATAx=0有解ξ,则
ξTATAξ=0,即(Aξ)T(Aξ)=0.
记Aξ=(ξ1,ξ2,…,ξn)T,则由上式得ξ21+ξ22+…+ξ2n=0,即ξ1=ξ2=…=ξn=0(利用ξ1,ξ2,…,ξn都为实数).所以有Aξ=0,即ξ也是方程Ax=0的解.因此选(C).
附注 本题表明:设A是n阶实矩阵,则Ax=0与ATAx=0是同解方程组.
这一结论可推广为:
设A是m×n实矩阵,B是n×l实矩阵,则Bx=0与ABx=0是同解方程组的充分必要条件是r(AB)=r(B).
(6)由于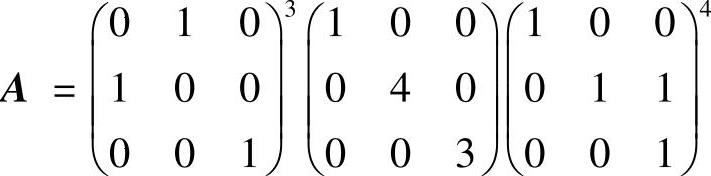
所以|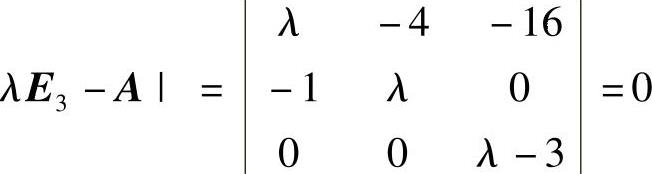 有解λ=-2,2,3.从而A的最小特征值为-2.因此选(B).
有解λ=-2,2,3.从而A的最小特征值为-2.因此选(B).
附注 题解中,由于注意到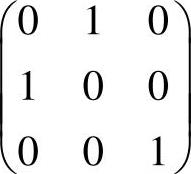 和
和 都是初等矩阵,它们的三次方与四次方分别左乘、右乘于
都是初等矩阵,它们的三次方与四次方分别左乘、右乘于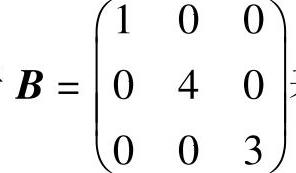 表明,对B施行三次“交换第1、2行”的初等变换后,再施行四次“将第2列加到第3列”的初等变换,所以很快获解.
表明,对B施行三次“交换第1、2行”的初等变换后,再施行四次“将第2列加到第3列”的初等变换,所以很快获解.
(7)记 ,则U的概率密度
,则U的概率密度
从而Z=X-2Y=X+U的概率密度为
因此选(B).
附注 常用的随机变量函数的概率密度计算公式:
(Ⅰ)设随机变量X的概率密度为f(x),记Y=g(X)(其中y=g(x)在f(x)≠0的区间内是单调函数,且除个别点外处处可导),则Y的概率密度为
其中I是g(x)在fX(x)≠0的区间上的值域,x=h(y)是y=g(x)在该区间的反函数.
(Ⅱ)设二维随机变量(X,Y)的概率密度为f(x,y),则随机变量Z=aX+bY+c(a,b,c都为常数)的概率密度为
当b≠0时,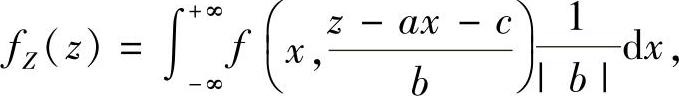
当a≠0时,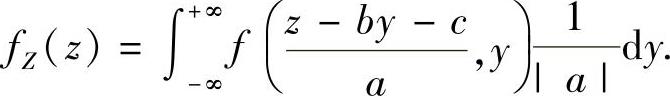
如果记住了(Ⅱ),则本题可快捷获解.
(8)由于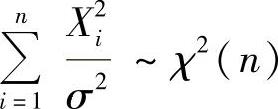 ,所以
,所以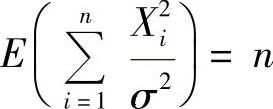 ,
, ,于是
,于是
因此选(D).
附注 应记住以下结论:
(Ⅰ)设X1,X2,…,Xn是来自总体X~N(μ,σ2)的简单随机样本,则
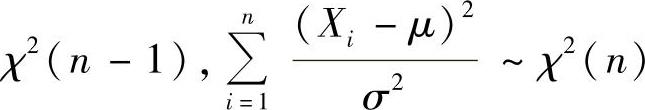 ,其中
,其中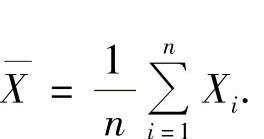
(Ⅱ)设X~χ2(n),则EX=n,DX=2n.
二、填空题
(9)由于f(x)在点x=0处连续,所以
其中,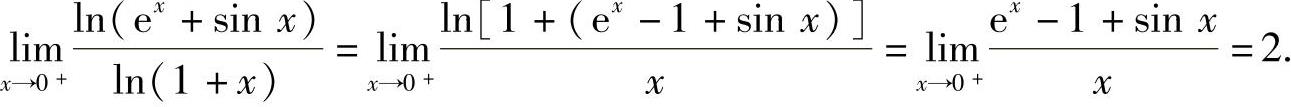 代入式(1)得a=e2.
代入式(1)得a=e2.
附注 (Ⅰ)计算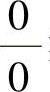 型未定式极限
型未定式极限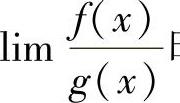 时,首先要对
时,首先要对 进行化简,其中对f(x)或g(x)作等价无穷小代替是最常用的,也是最有效的化简方法.
进行化简,其中对f(x)或g(x)作等价无穷小代替是最常用的,也是最有效的化简方法.
(Ⅱ)计算00,1∞,∞0型未定式极限lim[f(x)]g(x)时,应首先将函数指数化,即[f(x)]g(x)=eg(x)lnf(x),于是
(10)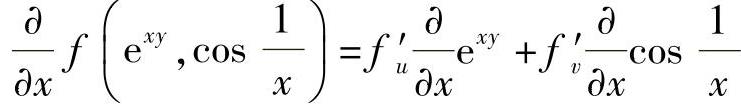
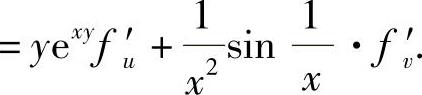
附注 计算多元复合函数的偏导数时,应先画出该函数与自变量之间的复合关系图,例如本题的关系图为
(11)由于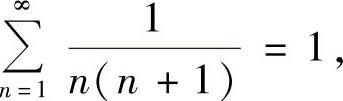
所以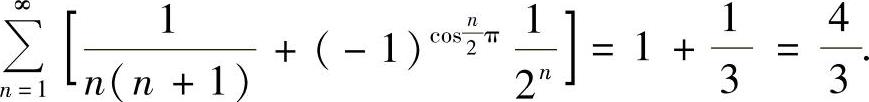
附注 应记住 .顺便计算
.顺便计算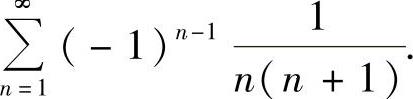
(12)由y″+py′+qy=0的通解可知,1+i是它的特征方程的根.所以y″+py′+qy=excosx的特解形式应为
xex(Acosx+Bsinx).
附注 对于2阶常系数非齐次线性微分方程
y″+py′+qy=f(x),当f(x)=eαx[Pl(x)cosβx+Qm(x)sinβx](Pl(x),Qm(x)分别是x的l次,m次多项式)时,该方程应有的特解形式为
y∗=xkeαx[R(1)n(x)cosβx+R(2)n(x)sinβx],
其中,k是按α+βi是特征方程λ2+pλ+q=0的零重根与一重根对应地取0,1,R(1)n(x),R(2)n(x)是x的n=max{l,m}次多项式.
(13)由于A∗=|A|A-1,其中
从而
附注 本题也可以利用以下公式,快捷算出A∗.
设A,B都是n阶可逆矩阵,则
(14)由于P(A)=C13p(1-p)2·p=3p2(1-p)2,则X的概率分布为
所以E(X2)=12·3p2(1-p)2=3p2(1-p)2.
附注 服从参数为λ的0-1分布的随机变量X的分布律为
由此可以算得X的数字特征,例如
EX=E(X2)=λ,D(X)=λ(1-λ)
等.
三、解答题
(15)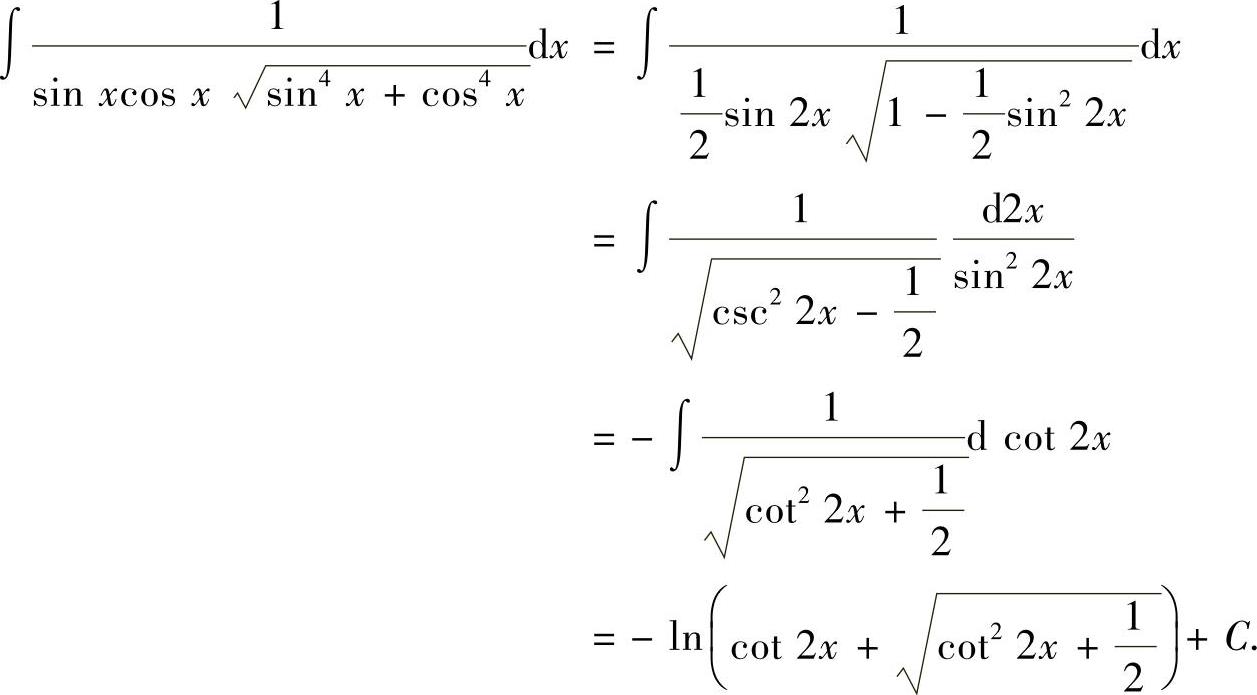
附注 可考虑类似的不定积分: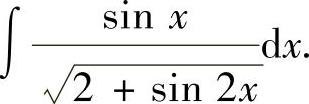 解答如下:
解答如下:
(16)由于fn(x)满足
f′n(x)-fn(x)=xn-1ex,
所以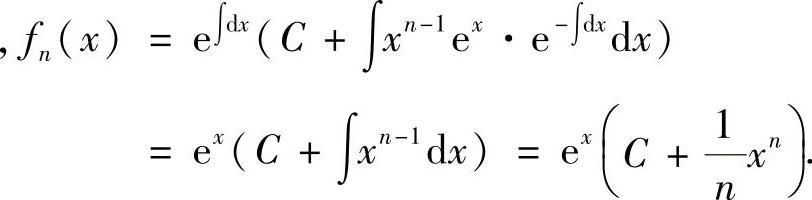
将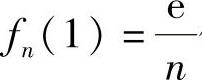 代入上式得C=0,所以
代入上式得C=0,所以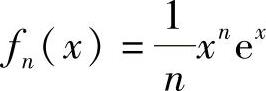 (n=1,2,…).从而(https://www.xing528.com)
(n=1,2,…).从而(https://www.xing528.com)
此外,s(0)=0.所以
附注 题解中直接利用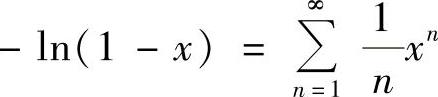 (x∈[-1,1)),比较快捷.
(x∈[-1,1)),比较快捷.
(17)由于 (其中,u=x-t),所以
(其中,u=x-t),所以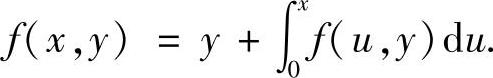 从而f(0,y)=y,且
从而f(0,y)=y,且
f′x(x,y)=f(x,y),
由此得到f(x,y)=yex.此外,由题设得
dg(x,y)=g′x(x,y)dx+g′y(x,y)dy=d(x+y),
所以g(x,y)=x+y+C0.从而由g(0,0)=0得C0=0.
g(x,y)=x+y.
由以上得到的f,g得
从而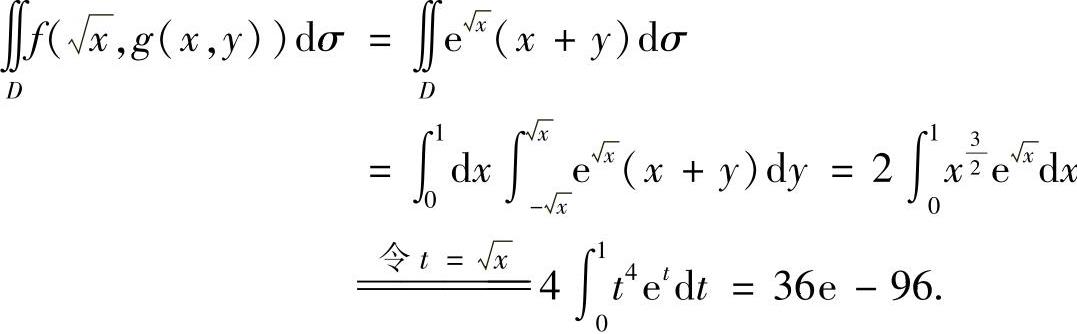
附注 题解中值得注意是:
为了对 的两边关于x求偏导数,需将被积函数中的x移走,故令u=x-t.
的两边关于x求偏导数,需将被积函数中的x移走,故令u=x-t.
(18)(Ⅰ) 如图答6-18所示.由于
如图答6-18所示.由于
图答 6-18
(Ⅱ)由于Σ: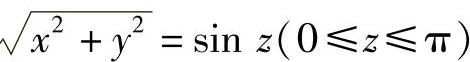 是闭曲面,所以
是闭曲面,所以
附注 题解中有两点值得注意:
(Ⅰ)由于 不是闭曲线,所以添上线段
不是闭曲线,所以添上线段 ,使得A
,使得A 成为闭曲线,然后应用格林公式计算所给的曲线积分,比较快捷.
成为闭曲线,然后应用格林公式计算所给的曲线积分,比较快捷.
(Ⅱ)由于Σ是闭曲面,且是外侧,所以对所给的曲面积分直接应用高斯公式计算,比较快捷.此外,计算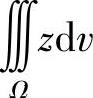 时,由于Ω是旋转曲面,且被积函数与x,y无关,所以采用先x,y,后z的方法.
时,由于Ω是旋转曲面,且被积函数与x,y无关,所以采用先x,y,后z的方法.
(19)c将[a,b]分成两个小区间[a,c]与[c,b].
由于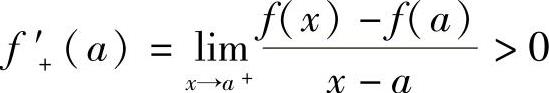 ,所以存在x1∈(a,c),使得f(x1)>f(a).由于
,所以存在x1∈(a,c),使得f(x1)>f(a).由于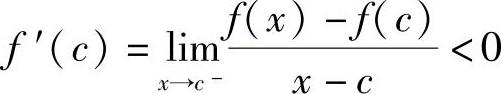 ,所以存在x2∈(x1,c),使得f(x2)>f(c).因此f(x)在[a,c]上的最大值在(a,c)内取到,于是由费马定理知,存在η1∈(a,c),使得f′(η1)=0.
,所以存在x2∈(x1,c),使得f(x2)>f(c).因此f(x)在[a,c]上的最大值在(a,c)内取到,于是由费马定理知,存在η1∈(a,c),使得f′(η1)=0.
此外,由f(c)=f(b)=0知,f(x)在[c,b]上满足罗尔定理条件,所以存在η2∈(c,b),使得f′(η2)=0.
由题设及以上证明知,f′(x)在[η1,η2]上满足罗尔定理条件,所以存在ξ∈(η1,η2)⊂(a,b),使得f″(ξ)=0.
附注 当函数f(x)在[a,b]上有连续导数时,如果f′+(a)·f′-(b)<0,则容易知道,存在ξ∈(a,b),使得f′(ξ)=0.但是,从本题的证明可知,“当f(x)在[a,b]上可导(未必有连续导数)时,如果f′+(a)·f′-(b)<0,则存在ξ∈(a,b),使得f′(ξ)=0.”记住这个结论,有助快捷解题.
(20)由于α1,α2,α3不能由β1,β2,β3线性表示,所以矩阵方程
(β1,β2,β3)X=(α1,α2,α3)
无解,从而
r(β1,β2,β3┈α1,α2,α3)>r(β1,β2,β3).
由于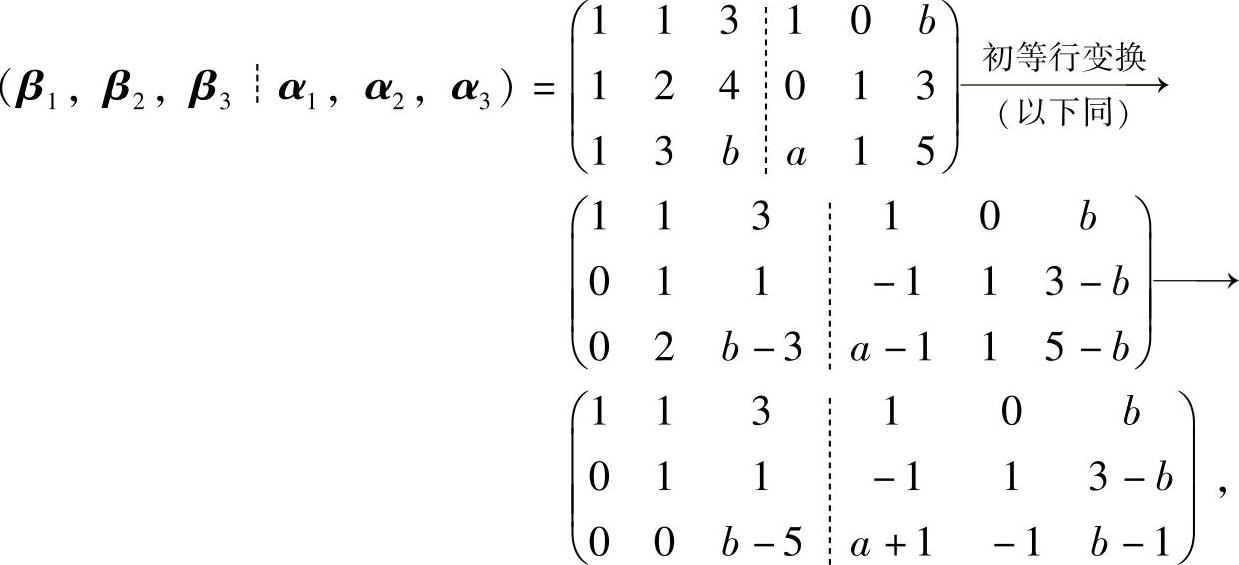
所以,b=5时,r(β1,β2,β3┈α1,α2,α3)=3>2=r(β1,β2,β3),即此时,α1,α2,α3不能由β1,β2,β3线性表示.
由于β1,β2,β3可由α1,α1+α2,α1+α2+α3线性表示,所以矩阵方程
(α1,α1+α2,α1+α2+α3)Y=(β1,β2,β3)有解,从而
r(α1,α1+α2,α1+α2+α3 β1,β2,β3)=r(α1,α1+α2,α1+α2+α3).将b=5代入得
β1,β2,β3)=r(α1,α1+α2,α1+α2+α3).将b=5代入得
所以,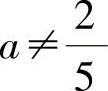 时,r(α1,α1+α2,α1+α2+α3┈β1,β2,β3)=r(α1,α1+α2,α1+α2+α3)(=3),即此时,β1,β2,β3可由α1,α1+α2,α1+α2+α3线性表示.于是,所求的
时,r(α1,α1+α2,α1+α2+α3┈β1,β2,β3)=r(α1,α1+α2,α1+α2+α3)(=3),即此时,β1,β2,β3可由α1,α1+α2,α1+α2+α3线性表示.于是,所求的 ,b=5.
,b=5.
附注 题解中有两点值得注意:
(Ⅰ)矩阵方程AX=B有解的充分必要条件是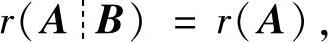 而无解的充分必要条件是
而无解的充分必要条件是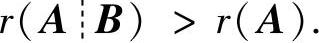
(Ⅱ)设有两个n维向量组(A):α1,α2,…,αr,(B):β1,β2,…,βs,则
(A)可由(B)线性表示,且表示式是唯一的充分必要条件是矩阵方程
(β1,β2,…,βs)X=(α1,α2,…,αr)(其中,X是未知矩阵)有唯一解;
(A)可由(B)线性表示,但表示式不唯一的充分必要条件是矩阵方程
(β1,β2,…,βs)X=(α1,α2,…,αr)有无穷多解;
(A)不可由(B)线性表示的充分必要条件是矩阵方程
(β1,β2,…,βs)X=(α1,α2,…,αr)
无解.
(21)由f(x1,x2,x3)在正交变换x=Qy下的标准形为y21+y22-y23知A有特征值λ1=λ2=1,λ3=-1,且对应λ3=-1的特征向量为α 设λ1=λ2=1对应的特征向量为α=(a1,a2,a3)T,则由A是实对称矩阵知,α与α3正交,即
设λ1=λ2=1对应的特征向量为α=(a1,a2,a3)T,则由A是实对称矩阵知,α与α3正交,即
a1+a3=0.
它的基础解系为α1=(0,1,0)T及α2=(-1,0,1)T,它们即为A的对应λ1=λ2=1的特征向量.α1,α2,α3是正交向量组,现将它们单位化:
它们是A的分别对应特征值为1,1,-1的特征向量.
由此可知A∗的特征值为
它们对应的特征向量分别为ξ1,ξ2,ξ3,记Q=(ξ1,ξ2,ξ3)(正交矩阵),则由A∗是实对称矩阵得
从而
附注 题解中有两点值得注意:
(Ⅰ)设A是n阶可逆矩阵,有特征值λ及对应的特征向量ξ,则A∗有特征值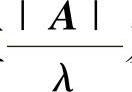 及对应的特征向量ξ.
及对应的特征向量ξ.
(Ⅱ)设A是可逆实对称矩阵,正交矩阵Q可使它正交相似对角化,则Q也可使A∗正交相似对角化.
(22)(Ⅰ)关于X的边缘概率密度
记Z的分布函数为F(z),则F(z)=P(Z≤z).
当z≤0时,P(Z≤z)=P(X2≤z)=0,
当0<z<1时,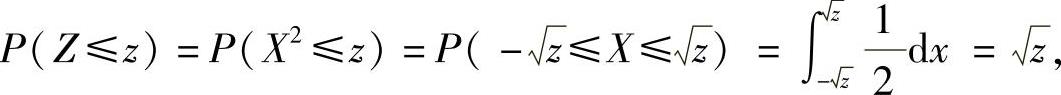
当z≥1时,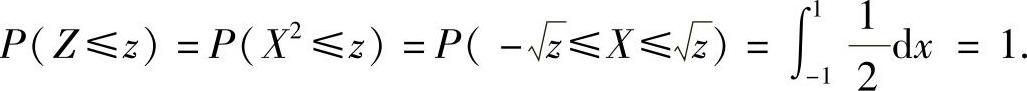
所以,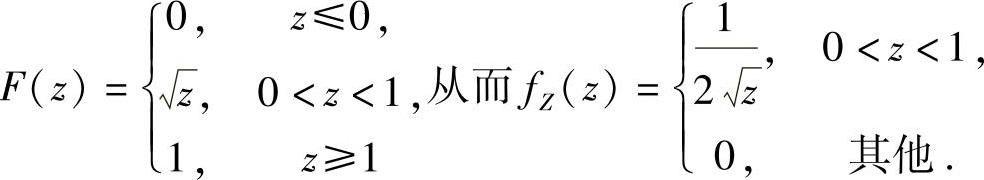
(Ⅱ)EW=E[(X-Y)2]=E(X2)+E(Y2)-2E(XY),
其中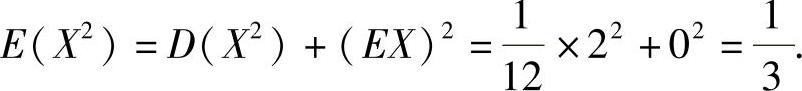 同样可得
同样可得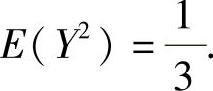 此外,
此外,
所以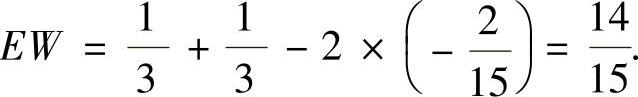
附注 E[(X-Y)2]也可按定义计算:
(23)(Ⅰ)由于N1~B(n,1-θ),N2~B(n,θ-θ2),N3~B(n,θ2),所以
EN1=n(1-θ),EN2=n(θ-θ2),EN3=nθ2.
因此,ET=E(a1N1+a2N2+a3N3)=a1EN1+a2EN2+a3EN3
=a1n(1-θ)+a2n(θ-θ2)+a3nθ2
=a1n+(-a1n+a2n)θ+(-a2n+a3n)θ2.
欲使T是θ的无偏估计量,必须ET=θ,即
a1n+(-a1n+a2n)θ+(-a2n+a3n)θ2=θ.
比较θ同次幂的系数得
(Ⅱ)由于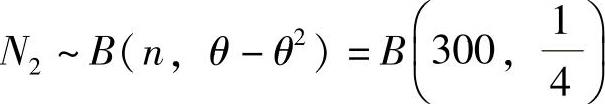 ,所以EN2=75,
,所以EN2=75,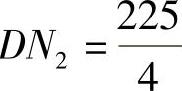 ,因此由中心极限定理(具体的是棣莫弗-拉普拉斯中心极限定理)知
,因此由中心极限定理(具体的是棣莫弗-拉普拉斯中心极限定理)知
附注 本题的关键,是从总体X的概率分布,推出Ni(i=1,2,3)的各自分布,即N1~B(n,1-θ),N2~B(n,θ-θ2),N3~B(n,θ2).
顺便计算T是θ的无偏估计量时的DT.
由于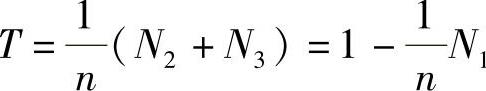 ,所以
,所以
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




