一、选择题
答案
(1)由于
所以,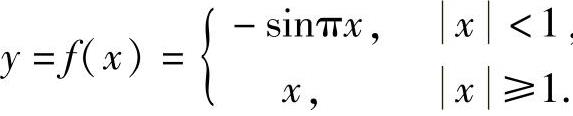 ,的图形如图答5-1所示,由图可知,f(x)的极大值为
,的图形如图答5-1所示,由图可知,f(x)的极大值为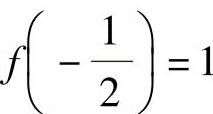 ,极小值为
,极小值为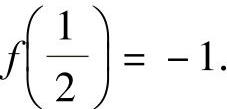 因此选(A).
因此选(A).
附注 画图得到正确选项,是解选择题常用的方法之一.
(2)选项(A)与(B)必有一个是不正确的.现按题设可得y=f(x)在点x0的邻域内的图形,如图答5-2所示,由图可知,f(x)在点x0不可导,因此选(B).
图答 5-1
图答 5-2
这与f(x)在点x0左侧邻近单调增加(即f(x)<f(x0))矛盾.由此证得f(x)在点x0处不可导.
显然证明是不易的,但在求解选择题时,是不必寻求这样复杂的证明,有时画出简图即可得到符合题意的选项.
(3)对于选项(D),由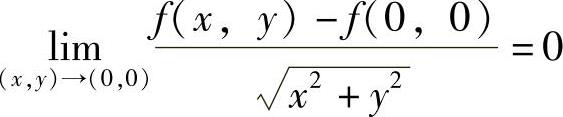 得
得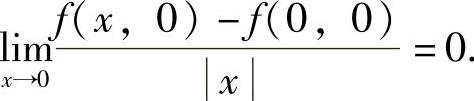 所以有
所以有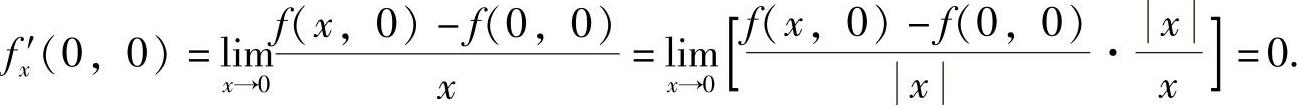 同样可得f′y(0,0)=0.于是由
同样可得f′y(0,0)=0.于是由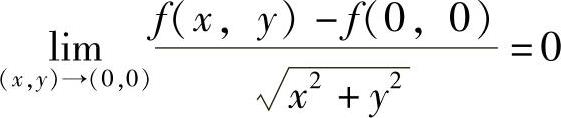 得
得
所以由二元函数可微的定义知,f(x,y)在点(0,0)处可微,因此选(D).
附注 显然,选项(A),(B)不是f(x,y)在点(0,0)处可微的充分条件.选项(C)也不是充分条件.例如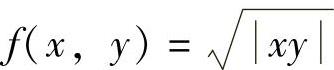 ,由
,由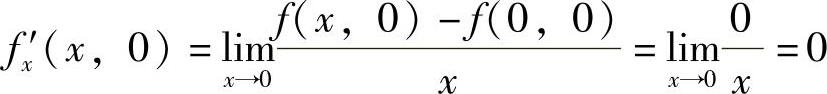 ,特别f′x(0,0)=0知,
,特别f′x(0,0)=0知, ,同样有
,同样有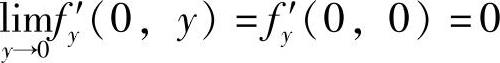 .但是由
.但是由
知,f(x,y)在点(0,0)处不可微.
(4)显然选项(A),(B)的微分方程不可能有特解y1,y2和y3.
由于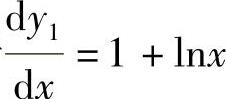 ,
,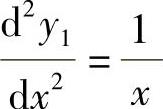 ,所以
,所以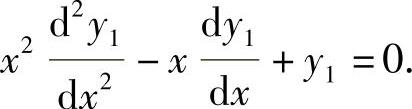
由于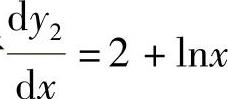 ,
,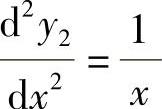 ,所以
,所以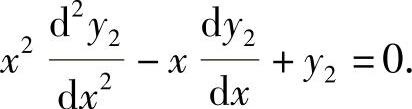
由于y3=3y1-y2,所以它必满足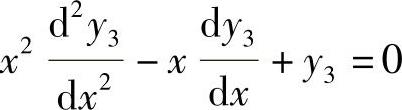 .因此选(C)
.因此选(C)
附注 (C)是正确的选项,也可如下证明:
令x=et,则y1=tet,y2=tet+et,y3=2tet-et,选项(C)中的微分方程(欧拉方程)成为
由于(1)的特征方程λ2-2λ+1=0有根λ=1(二重),所以选项(C)的方程有特解y1,y2,y3.
(5)由于选项(C)与(D)有且仅有一个是正确的,因此只要考虑这两个选项即可.由r(B)=r(A)≤n<n+1知,By=0有非零解.因此选(C).
附注 设A是m×n矩阵,则
r(A)=n是齐次线性方程组Ax=0只有零解的充分必要条件;
r(A)<n是齐次线性方程组Ax=0有非零解的充分必要条件.
(6)A有特征值-1,1,2.由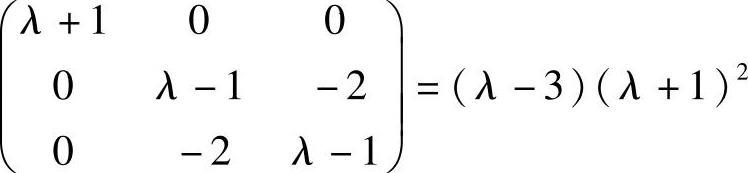 知,选项(A)的矩阵
知,选项(A)的矩阵 有特征值λ=3,-1(二重),它与A有不同的特征值,故不与A相似,从而不能选(A).
有特征值λ=3,-1(二重),它与A有不同的特征值,故不与A相似,从而不能选(A).
对于选项(B)的矩阵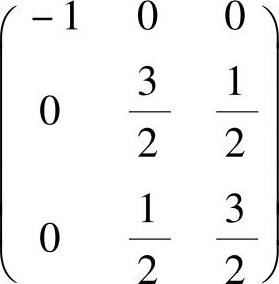 ,由
,由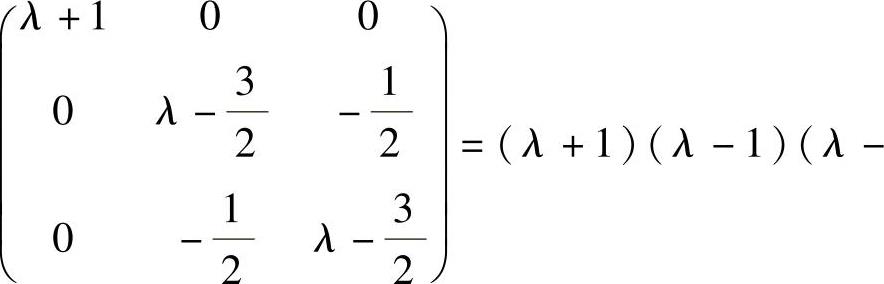
3)知,它有特征值-1,1,2,即与A有相同的特征值,所以这个实对称矩阵与A相似且合同.因此选(B).
附注 (Ⅰ)设A与B都是n阶矩阵,则A与B相似的充分必要条件有以下两类:
(i)存在n阶可逆矩阵P,使得P-1AP=B;
(ii)A与B有相同的特征多项式,或者A与B有相同的特征值(ni重以ni个计算).
(Ⅱ)设A与B都是n阶实对称矩阵,则A与B合同的充分必要条件有以下三类:
(i)存在n阶可逆矩阵C,使得CTAC=B;
(ii)二次型xTAx与xTBx(其中x=(x1,x2,…,xn)T)有相同的规范形,或者二次型xTAx与xTBx有相同的正惯性指数,也有相同的负惯性指数;
(iii)A与B有相同的特征值(ni重的以ni个计算).
(7)记Y的分布函数为FY(y),则
所以,Y的分布函数FY(y)只有一个间断点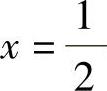 .因此选(B).
.因此选(B).
附注 由于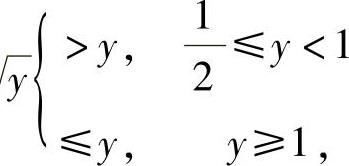 ,所以
,所以
(8)记U=X1+X2+X5+X6,V=X3+X4-X7-X8,则U~N(0,4σ2),V~N(0,4σ2),所以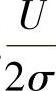 ,
,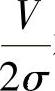 相互独立,且都服从N(0,1),由此得到
相互独立,且都服从N(0,1),由此得到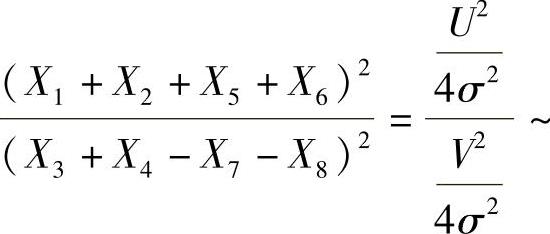
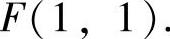 因此选(C).
因此选(C).
附注 F(n1,n2)分布定义如下:
设X~χ2(n1),Y~χ2(n2),且X与Y相互独立,则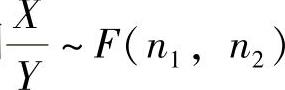 .
.
二、填空题
(9)所给方程两边对x求导得
即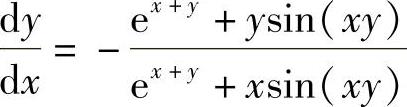 ,且
,且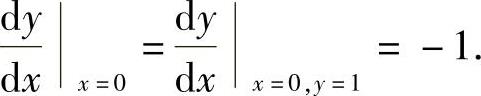
于是,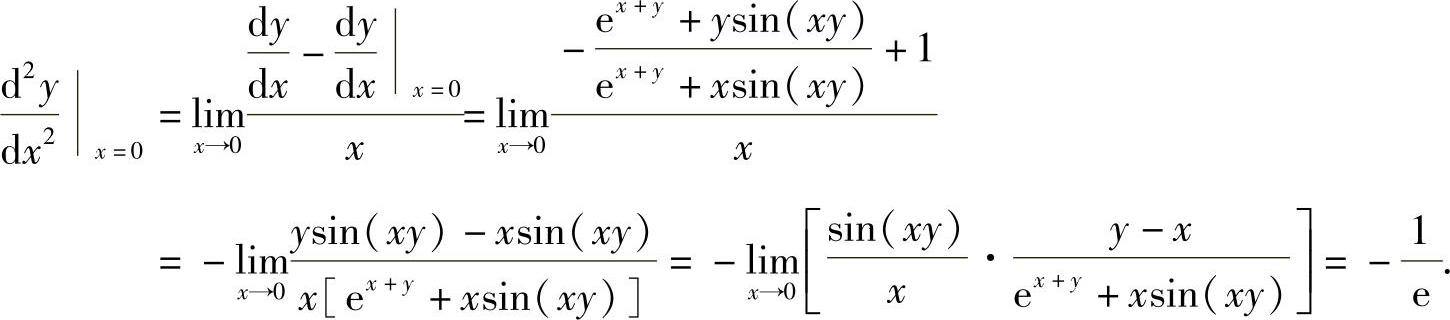
附注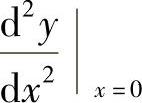 也可以由
也可以由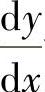 计算出
计算出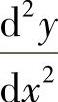 ,然后将x=0,y=1,
,然后将x=0,y=1,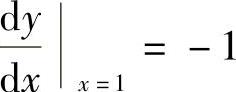 代入得到,但这样计算比较繁复,没有题解中采用的方法简捷.
代入得到,但这样计算比较繁复,没有题解中采用的方法简捷.
(10)
附注 由于ecosxsinx是奇函数,所以题解中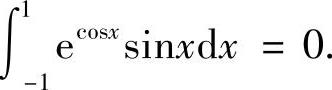
(11)由于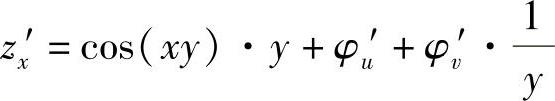 ,所以
,所以
附注 要熟练掌握二元复合函数的1、2阶偏导数的计算.
(12)所给微分方程
y″+2y′+y=2e-x+x (1)
对应的齐次微分方程y″+2y′+y=0的通解为
Y=(C1+C2x)e-x.
此外,式(1)有特解
y∗=Ax2e-x+B+Cx.
将它代入式(1)得
(2Ae-x-4Axe-x+A2x2e-x)+2(2Axe-x-Ax2e-x+C)+(Ax2e-x+B+Cx)=2e-x+x.由此得到A=1,B=-2,C=1,所以
y∗=x2e-x-2+x.
因此式(1)的通解为
y=Y+y∗=(C1+C2x)e-x+x2e-x-2+x.
附注 由于式(1)的右边为2e-x与x两项之和,其中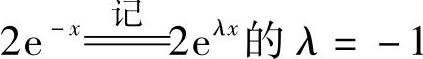 是齐次方程y″+2y′+y=0的特征方程λ2+2λ+1=0的二重根,所以y″+2y′+y=2e-x有形如Ax2e-x的特解.此外,y″+2y′+y=x有形如B+Cx的特解.从而式(1)有形如y∗=Ax2e-x+B+Cx的特解.
是齐次方程y″+2y′+y=0的特征方程λ2+2λ+1=0的二重根,所以y″+2y′+y=2e-x有形如Ax2e-x的特解.此外,y″+2y′+y=x有形如B+Cx的特解.从而式(1)有形如y∗=Ax2e-x+B+Cx的特解.
(13)由于r(A)=r(AB)≤r(B),即r(A)≤r(B). (1)
此外,由r(A)=n及r(A)+r(B)-n≤r(AB)≤r(A)得r(B)≤r(A). (2)
所以由式(1)、式(2)得r(B)=r(A)=n.从而r(B∗)=n.
附注 题解中利用了关于矩阵秩的以下结论:
(Ⅰ)设A是m×n矩阵,B是n×l矩阵,则
r(A)+r(B)-n≤r(AB)≤min{r(A),r(B)}.
(Ⅱ)设A是n阶矩阵,则
(14)由题设知,X,Y相互独立,从而X与Y2相互独立,且X的概率密度为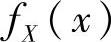
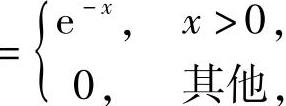 y的概率密度为
y的概率密度为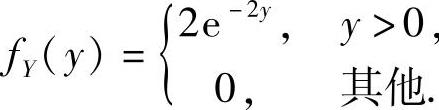 所以D(X+Y2)=DX+D(Y2),其中
所以D(X+Y2)=DX+D(Y2),其中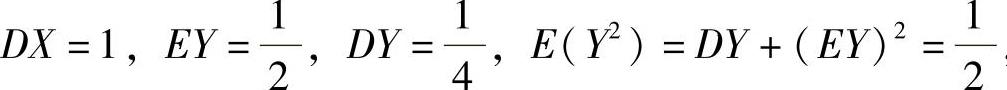 ,并且
,并且
因此,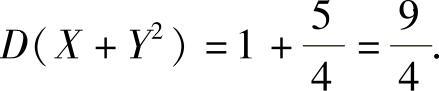
附注 记住:服从参数为λ(λ>0)的指数分布的随机变量X的概率密度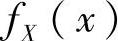
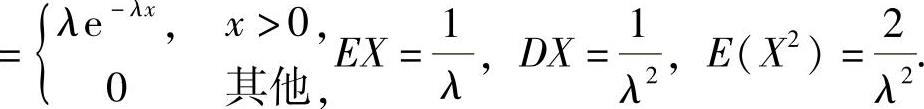
三、解答题
(15)由于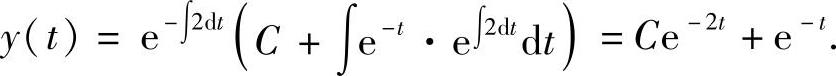 将y(0)=0代入上式得C=-1.所以y(t)=-e-2t+e-t(t≥0).
将y(0)=0代入上式得C=-1.所以y(t)=-e-2t+e-t(t≥0).
当t<0时,f′(t)=(2t2+sint)′=4t+cost,
当t>0时,f′(t)=y′(t)=(-e-2t+e-t)′=2e-2t-e-t.
由于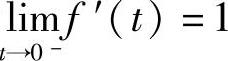 ,
,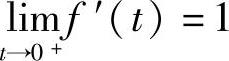 ,所以f′(0)=1.因此
,所以f′(0)=1.因此
由此可得,t<0时,f″(t)=4-sint;t>0时,f″(t)=-4e-2t+e-t.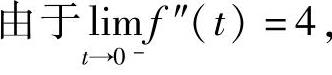
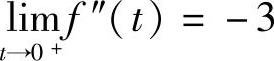 ,所以f″(0)不存在,因此
,所以f″(0)不存在,因此
附注 f′(0)=1与f″(0)不存在也可证明如下:(https://www.xing528.com)
由于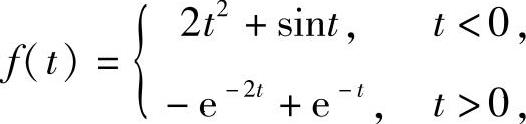 所以
所以
从而f′(0)=1.
由于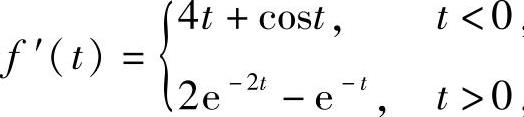 ,所以
,所以
从而f″(0)不存在.
(16)令u=x-t,则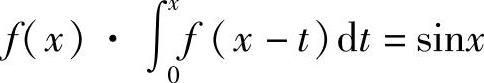 成为
成为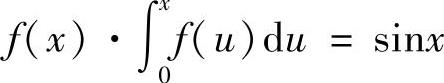 ,即
,即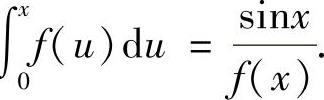
上式两边对x求导得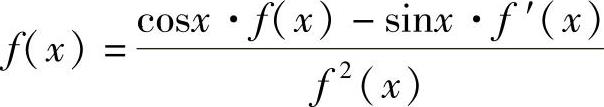 ,即
,即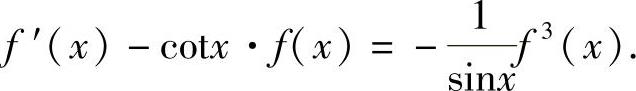 令
令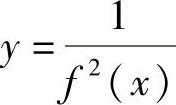 ,得
,得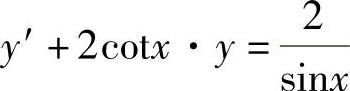 ,所以
,所以
将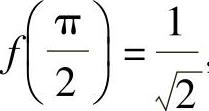 ,即
,即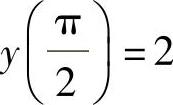 代入上式得C=2,所以,在
代入上式得C=2,所以,在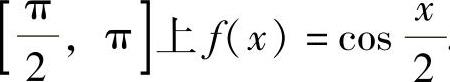 .因此f(x)在
.因此f(x)在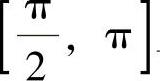 上的平均值为
上的平均值为
附注 y′+p(x)y=q(x)yn(n≠0,1)称为伯努利方程,它可通过变量代换z=y1-n转换成线性方程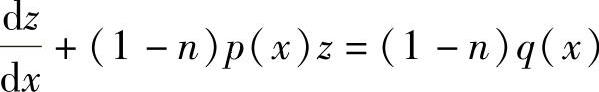 后求解.
后求解.
(17)u(x,2x)=x两边对x求导得u′x(x,2x)+2u′y(x,2x)=1.
再对x求导得[ux″x(x,2x)+2u″xy(x,2x)]+2[u″yx(x,2x)+2u″yy(x,2x)]=0,
利用u″xx=u″yy,u″xy=u″yx化简后得
5u″xx(x,2x)+4u″xy(x,2x)=0. (1)
u′x(x,2x)=x2两边对x求导得
u″xx(x,2x)+2u″xy(x,2x)=2x. (2)
由式(1),式(2)得u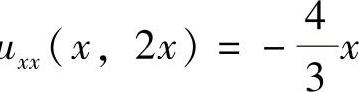 ,
,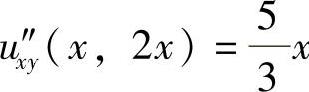 .于是D如图答5-17阴影部分所示,所以D的面积为
.于是D如图答5-17阴影部分所示,所以D的面积为
附注 本题获解的关键是利用题设从u(x,2x)=x,u′x(x,2x)=x2中算出u″xx(x,2x)与u″xy(x,2x)的表达式,这一点可以如题解中那样,将以上两式对x求导即可.
图答 5-17
(18)所给不等式可改写成
(f′(x)-3f(x))′-2(f′(x)-3f(x))>0. (1)
式(1)两边同乘以e-2x得
e-2x(f′(x)-3f(x))′-e-2x·2(f′(x)-3f(x))>0,
即[e-2x(f′(x)-3f(x))]′>0.
所以,对x>0有
e-2x(f′(x)-3f(x))>[e-2x(f′(x)-3f(x))]|x=0=-3,
即e-2x(f′(x)-3f(x))+3>0. (2)
式(2)两边同乘以e-x得
[e-3xf′(x)-3e-3xf(x)]+3e-x>0,
即(e-3xf(x)-3e-x)′>0.
所以,对x>0有
e-3xf(x)-3e-x>(e-3xf(x)-3e-x)x=0=-2,
即f(x)>3e2x-2e3x(x>0).
附注 题解中,值得注意的是:式(1)两边同乘以e-2x,使其左边成为一个函数的导数;同样,在式(2)两边同乘以e-x,使其左边也成为一个函数的导数.
(19)
其中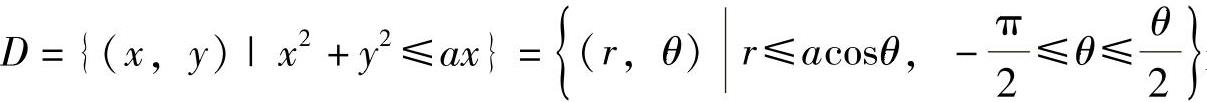 是Σ在xOy平面上的投影,且
是Σ在xOy平面上的投影,且
所以
附注 设曲面Σ:z=z(x,y),且f(x,y,z)是连续函数,则
其中,Dxy是Σ在xOy平面上的投影.
(20)由于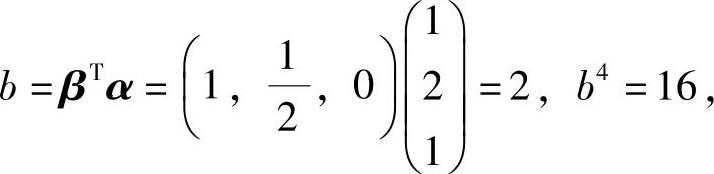
所以,所给的方程组成为
(8A-16E3)x=γ,即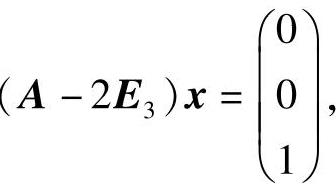
或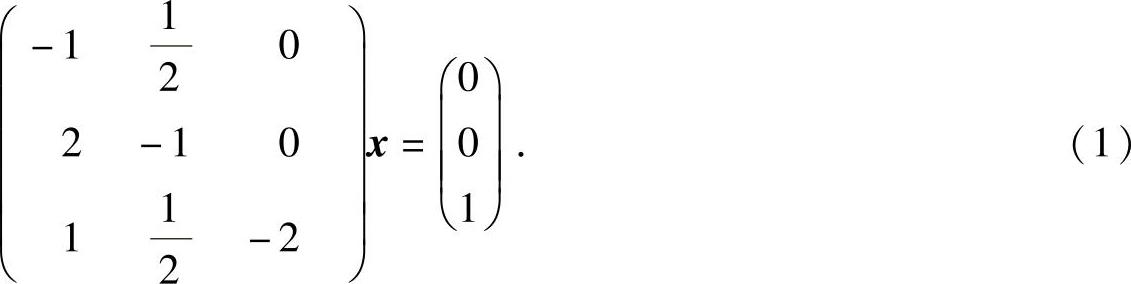
由于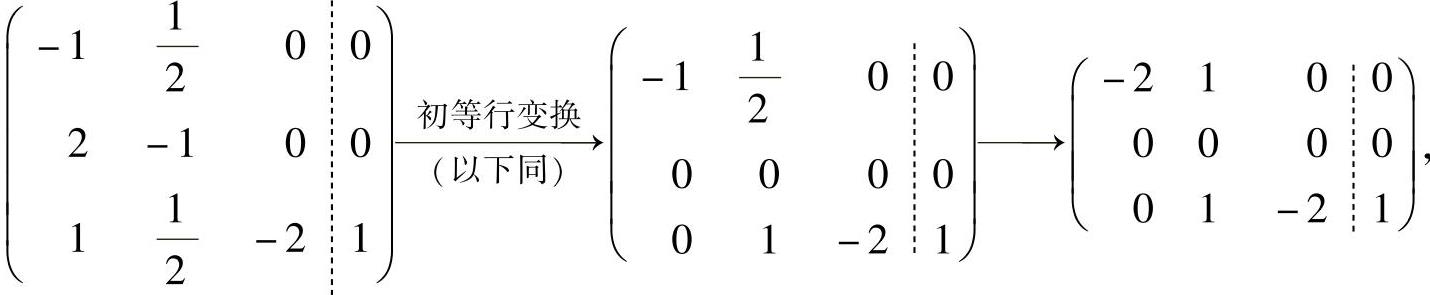
所以,式(1)与方程组 同解.式(2)的导出组的通解为C(1,2,1)T,此外式(2)有特解
同解.式(2)的导出组的通解为C(1,2,1)T,此外式(2)有特解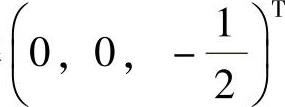 ,所以,式(2),即所给方程组的通解
,所以,式(2),即所给方程组的通解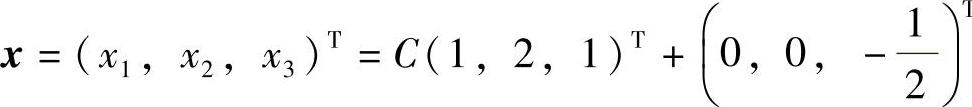 (其中,C是任意常数).
(其中,C是任意常数).
附注 设α,β都是n维列向量,则αTβ是一个常数,记为c;αβT是n阶矩阵,记为A,则r(A)≤1,且对正整数k,有
(21)由于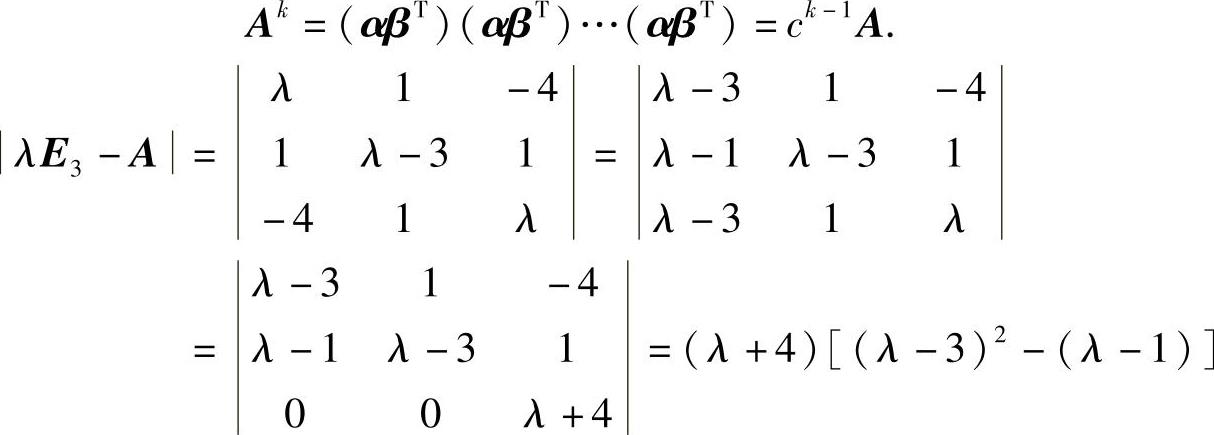
=(λ-2)(λ-5)(λ+4),
所以A有特征值λ=2,5,-4.
设对应λ=2的特征向量为a=(a1,a2,a3)T,则a满足
由于
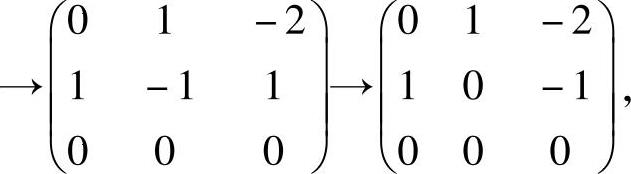
所以,式(1)与方程组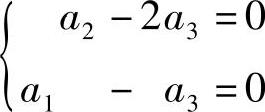 ,同解,故可取a为它的基础解系,即a=(1,2,1)T.设对应λ=5的特征向量为b=(b1,b2,b3)T,则b满足
,同解,故可取a为它的基础解系,即a=(1,2,1)T.设对应λ=5的特征向量为b=(b1,b2,b3)T,则b满足
由于 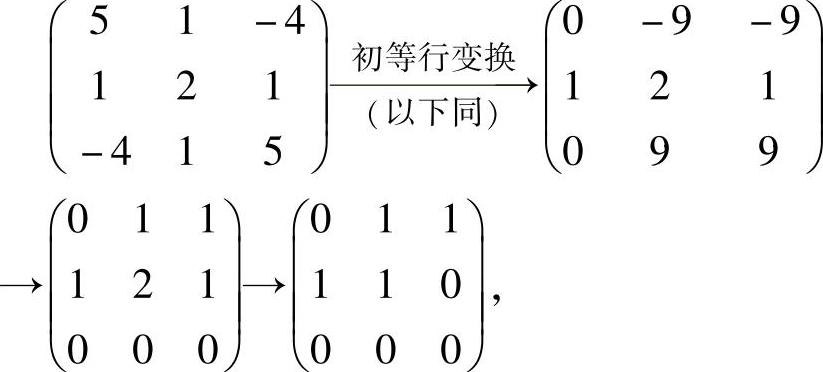
所以式(2)与方程组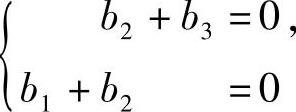 同解,故可取b为它的基础解系,即b=(1,-1,1)T.
同解,故可取b为它的基础解系,即b=(1,-1,1)T.
设对应λ=-4的特征向量为c=(c1,c2,c3)T,则由A是实对称矩阵知,c与a,b都正交,所以有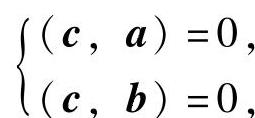 即
即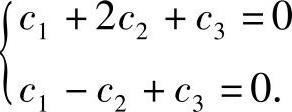 ,由于它与
,由于它与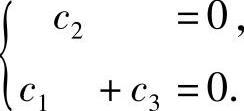
同解,故可取c为它的基础解系,即c=(1,0,-1)T.
显然a,b,c是正交向量组,现将它们单位化:
记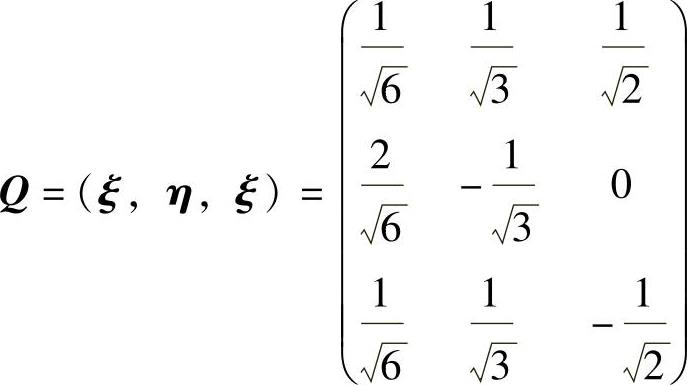 (正交矩阵),则
(正交矩阵),则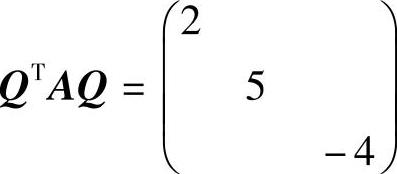 ,于是在
,于是在
正交变换x=Qy下,f(x1,x2,x3)=2y21+5y22-4y23(标准形).
由QTA∗Q=QTAA-1Q=-40Q-1A-1Q(A=2×5×(-4)=-40)
=-40(Q-1AQ)-1=-40(QTAQ)-1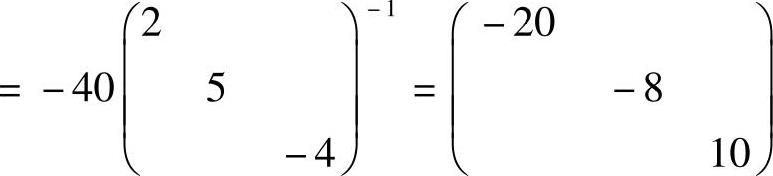 知,在正交变换x=Qy下,
知,在正交变换x=Qy下,
f2(x1,x2,x3)=xTA∗x=yT(QTA∗Q)y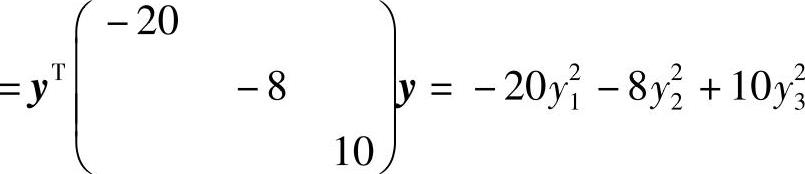 (标准形).
(标准形).
附注 由题解可知,如果A是n阶可逆实对称矩阵,则当正交变换x=Qy将二次型f1(x1,x2,…,xn)=xTAx(其中x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T)化为标准形λ1y21+λ2y22+…+λny2n(其λ1,λ2,…,λn是A的特征值)时,必将二次型f2(x1,x2,…,xn)=xTA∗x化为标准形μ1y21+μ2y22+…+μny2n(其中μ1,μ2,…,μn是A∗的特征值).记住这个结论,是有用的.
(22)(Ⅰ)记Y的分布函数为FY(y),则
FY(y)=P(Y≤y)=P(X2≤y).
当y≤0时,P(X2≤y)=0;
当0<y≤1时,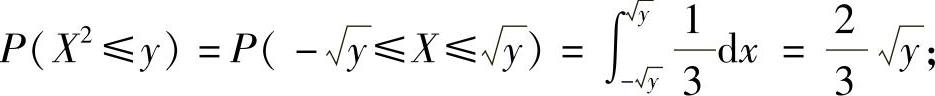
当1<y≤4时,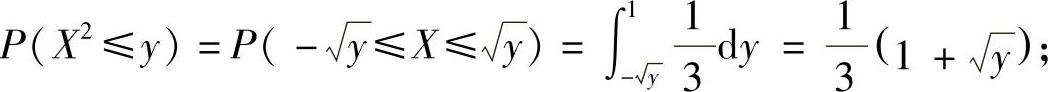
当y>4时,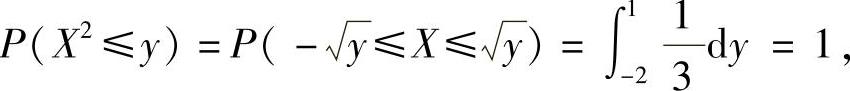
所以,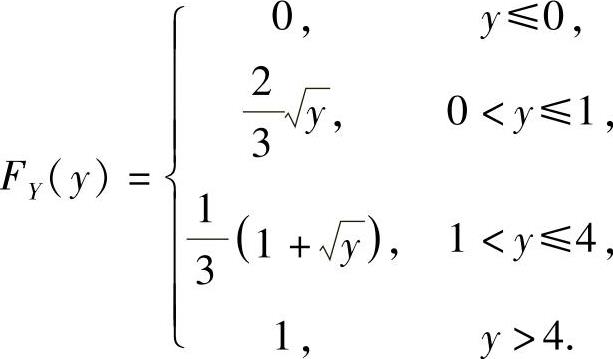 由此得到
由此得到
(Ⅱ)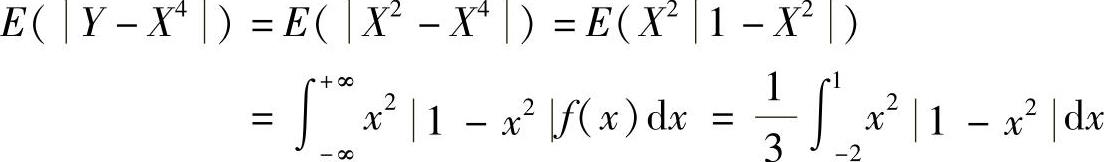
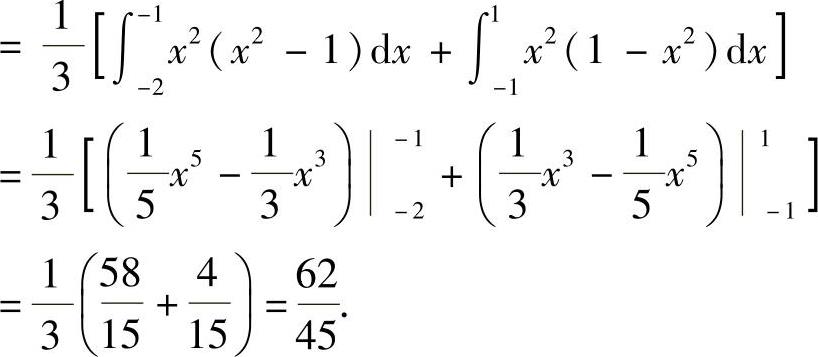
附注 φ(y)也可以按以下方法计算:
由于y=x2在f(x)≠0的区间[-2,0)与(0,1]上都是单调的,且y=x2在(-2,0)内的反函数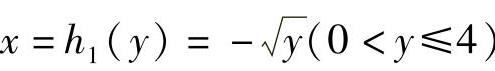 ,在(0,1)内的反函数
,在(0,1)内的反函数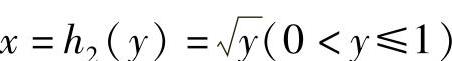 ,所以
,所以
(23)设所给的随机简单样本的观察值为x1,x2,…,xn.为了计算θ的最大似然估计量,可认为x1,x2,…,xn全为正的.故似然函数为
即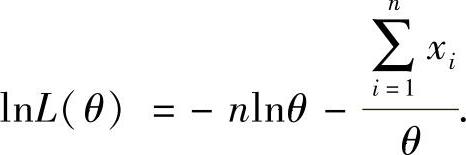 于是由
于是由
得θ的最大似然估计值为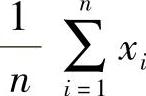 ,从而θ的最大似然估计量为
,从而θ的最大似然估计量为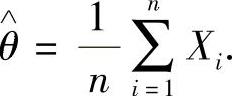 由于EX=θ,DX=θ2,所以由
由于EX=θ,DX=θ2,所以由
由此可知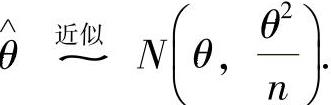
附注 设Y是随机变量,如果对于任意实数y有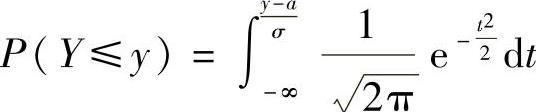 ,则Y~N(a,σ2);如果对任意实数y有
,则Y~N(a,σ2);如果对任意实数y有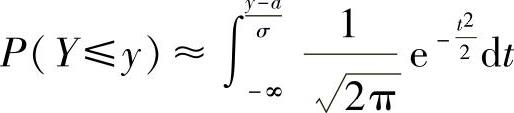 ,则
,则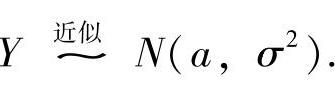
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




