一、选择题
答案
(1)由(x0,f(x0))是曲线y=f(x)的拐点知,(x0,-f(x0))是曲线y=-f(x)的拐点.因此选(B).
附注 实际上,(-x0,f(x0))是曲线y=f(-x)的拐点,(-x0,-f(x0))是曲线y=-f(-x)的拐点.
(2)在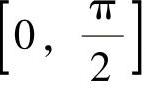 上,sin(sinx)≤sinx(仅在点x=0处取等号),cos(sinx)≥cosx(仅在点x=0处取等号),所以
上,sin(sinx)≤sinx(仅在点x=0处取等号),cos(sinx)≥cosx(仅在点x=0处取等号),所以
故有I1<I3.因此选(B)
附注 选项(A)是不正确的,这是由于
即I1=I2.
(3)当(x,y)≠(0,0)时,
并且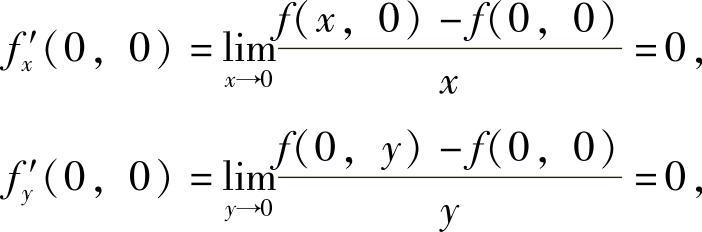
所以,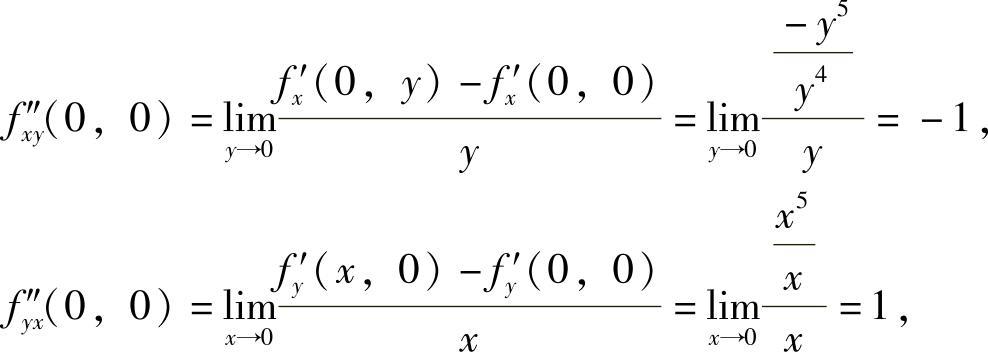 故f″xy(0,0)<f″yx(0,0).因此选(C).
故f″xy(0,0)<f″yx(0,0).因此选(C).
附注 在已算出f′x(x,y)时,可按以下方法快捷算出f′y(x,y):
当φ(y,x)=-φ(x,y)时,φ′y(x,y)=-φ′x(y,x).
因此本题有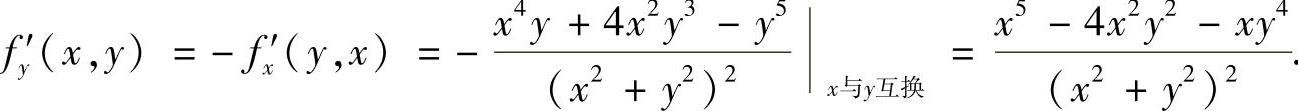
(4)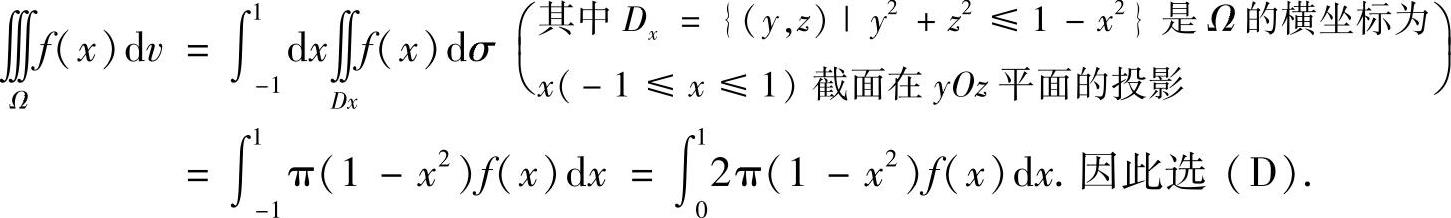
附注 由于Ω的横坐标为x的截面为圆,所以对所给的三重积分采用“先二后一”方法进行计算.
(5)由于
所以,t=2时,|(α1,α2,α3,α4)|=0,即α1,α2,α3,α4线性相关;t=3时,|(α1,α2,α3,α4)|≠0,即α1,α2,α3,α4线性无关.由此可知,结论①④正确,因此选(C).
附注 确定n个n维列向量α1,α2,…,αn的线性相关性的好方法是计算行列式D=|(α1,α2,…,αn)|.如果D=0,则α1,α2,…,αn线性相关;如果D≠0,则α1,α2,…,αn线性无关.
(6)由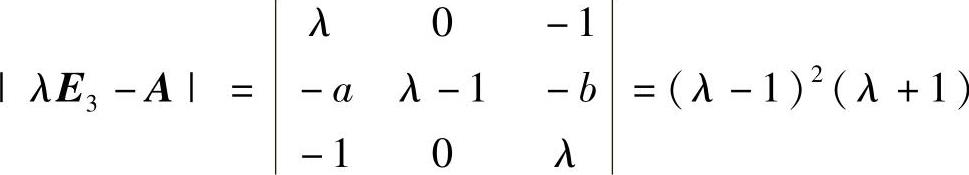 知,A的特征值为λ=1(二重),λ=-1.
知,A的特征值为λ=1(二重),λ=-1.
由于A可相似对角化,所以r(1·E3-A)=3-2=1,即
用-b-1代替b,A就成为B,所以由B可相似对角化得
-a=-b-1.(2)
由式(1),式(2)得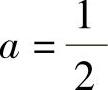 ,
,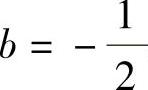 .因此选(A).
.因此选(A).
附注 设A是n阶矩阵,则A可相似对角化的充分必要条有较多种,其中常用的有:
设A有特征值λ1,λ2,…,λs,它们的重数分别为n1,n2,…,ns(n1+n2+…+ns=n),则A可相似对角化充分必要条件为
r(λiEn-A)=n-ni(i=1,2,…,s)
(7)由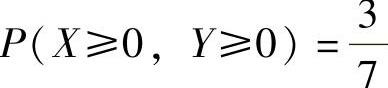 ,
,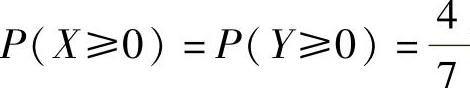 得
得
所以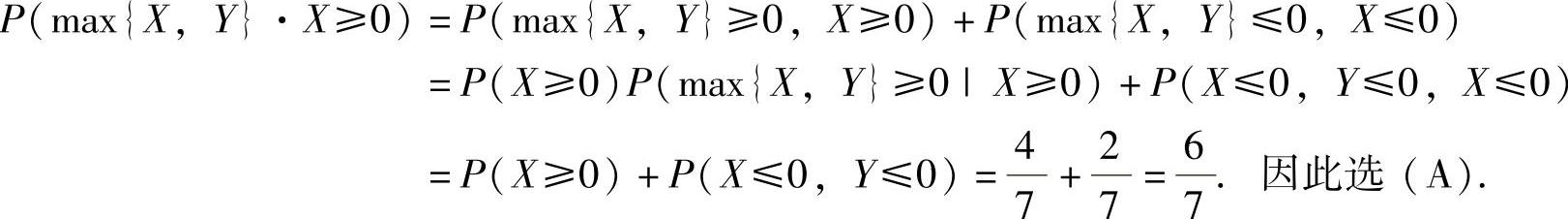
附注 题解中有两点值得注意
(Ⅰ)由于X,Y是连续型随机变量,所以P(X≤0,Y≤0)=P(X<0,Y<0).
(Ⅱ)由于X≥0时,必有max{X,Y}≥0,所以P(max{X,Y}≥0|X≥0)=1.
(8)由题设知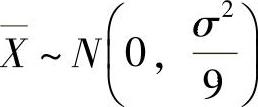 ,所以
,所以
由于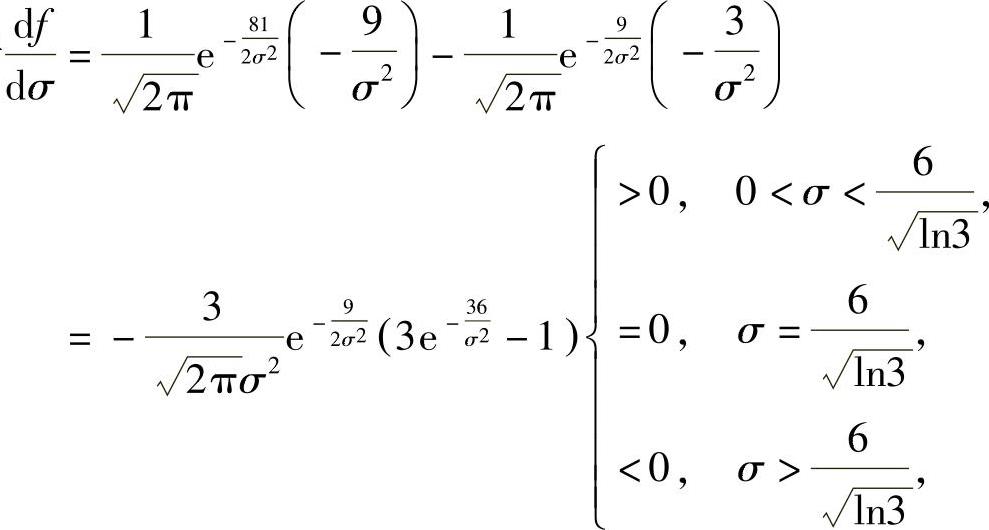
所以,使得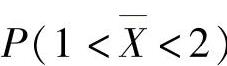 为最大的
为最大的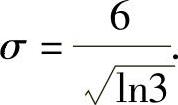 因此选(C).
因此选(C).
附注 应记住以下结论:
设X1,X2,…,Xn是来自总体X的简单随机样本,记μ=EX,σ2=DX,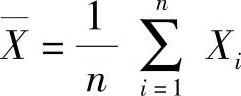 (样本均值),
(样本均值),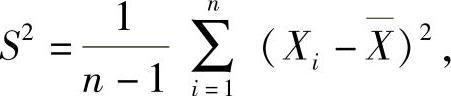
于是,当X~N(μ,σ2)时,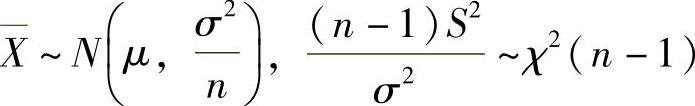 ,并且
,并且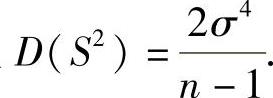
二、填空题
(9)由于(sinx3)3是奇函数,所以它在点x=0处的4阶导数为0.
由于(lncosx)′=-tanx,(lncosx)″=(-tanx)′=-sec2x,(lncosx)(3)=(-sec2x)′=-2sec2xtanx,
所以,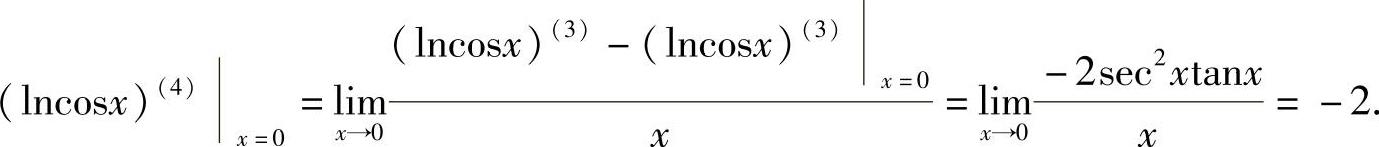
从而,f(4)(0)=0+(-2)=-2.
附注 设f(x)在点x=0处任意阶可导,则
当f(x)是奇函数时,f(2k)(0)=0(k=0,1,2,…);
当f(x)是偶函数时,f(2k+1)(0)=0(k=0,1,2,…).
(10)令x=et,则t=lnx,于是有
将它们代入所给微分方程得
式(1)的齐次方程的通解为Y=C1+C2e2t.式(1)有特解y∗=t(A+Bt),将它代入式(1)得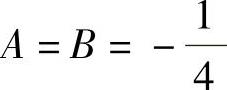 ,即
,即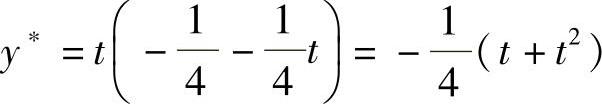 ,所以式(1)的通解为
,所以式(1)的通解为
从而所求的通解为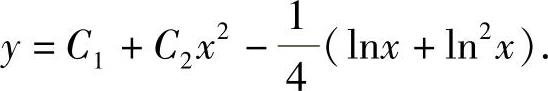
附注 x2y″+axy′+by′=f(x)是2阶欧拉方程,令x=et可转化成2阶常系数线性微分方程
(11)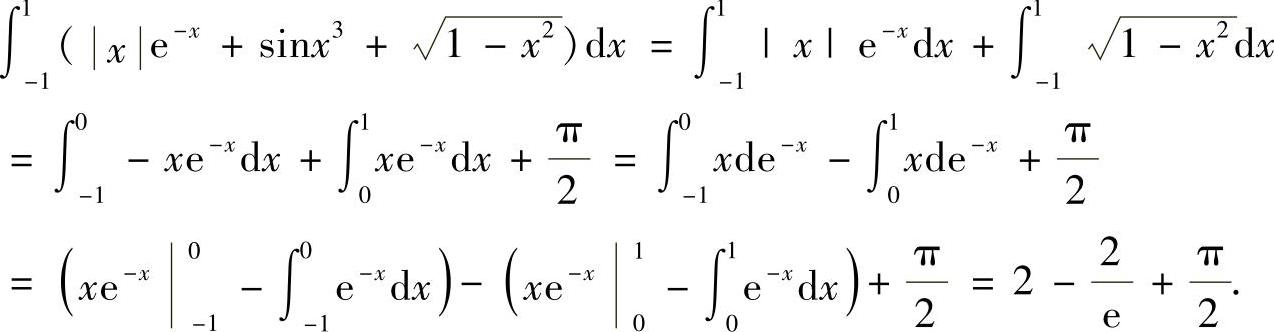
附注 利用定积分几何意义,有
(12)由于C关于x轴对称,在对称点处xy互为相反数,所以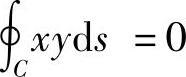 .此外,C的极坐标方程为
.此外,C的极坐标方程为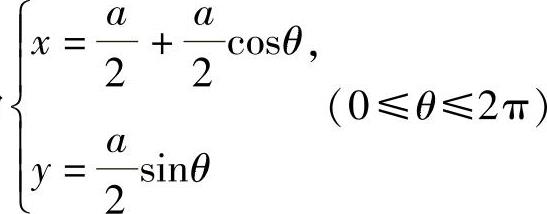 .因此
.因此
于是,由题得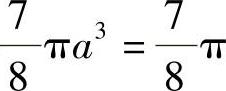 ,从而a=1.
,从而a=1.
附注 利用曲线C的对称性,可以化简关于弧长的曲线积分的计算:
设f(x,y)连续,曲线C具有某种对称性,则
其中C1是C按其所具有的对称性被划分成的两部分之一.
(13)由题设得
记P=(α1,α2,α3),则由α1,α2,α3线性无关知P可逆,且式(1)可以表示为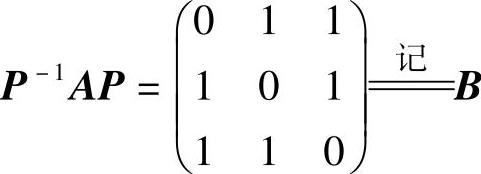 ,所以A~B.从而A与B有相同的特征值.
,所以A~B.从而A与B有相同的特征值.
由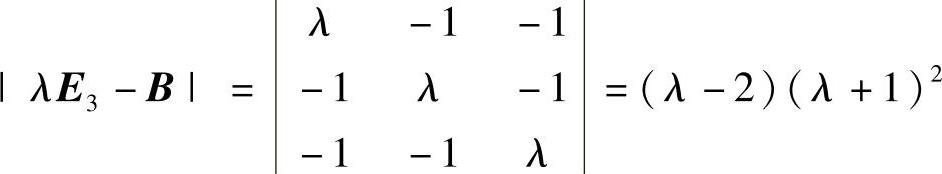 知,B的最大特征值为2,从而A的最大特征值为2.
知,B的最大特征值为2,从而A的最大特征值为2.
附注 设A与B都是n阶矩阵,如果它们相似,则
(Ⅰ)A=B.
(Ⅱ)r(A)=r(B),从而A与B等价.
(Ⅲ)A,B有相同的特征值.
(Ⅳ)A∗~B∗.
(Ⅴ)当A可逆时,B也可逆,且A-1~B-1.
(14)记X={乙箱中的次品数},
Y={从乙箱中取出的次品数},
则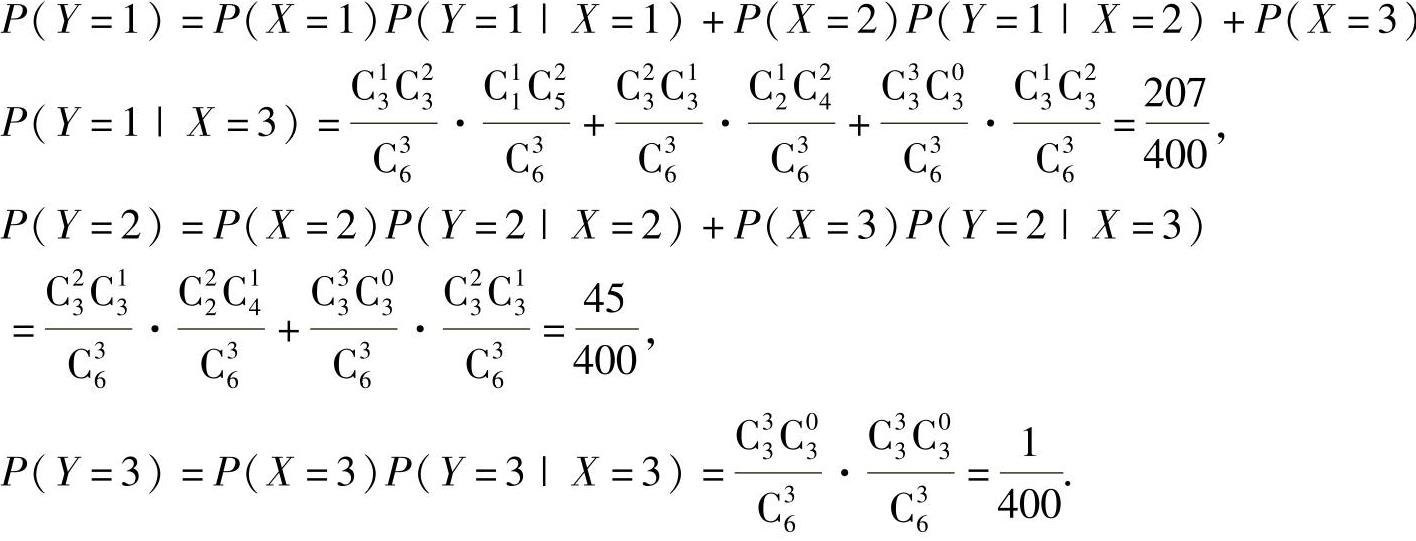
所以,所求的平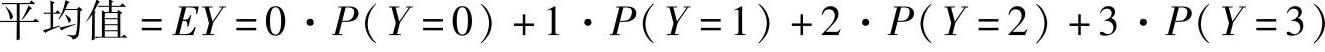
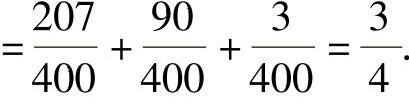
附注 由于Y可能取的值为0,1,2,3,所以
EY=0·P(Y=0)+1·P(Y=1)+2·P(Y=2)+3·P(Y=3).但是,在具体计算时,P(Y=0)是不必算出的.(https://www.xing528.com)
三、解答题
(15)由f(x)在点x=1处左连续知,
附注 题解中有两点值得注意:
(Ⅰ)作变量代换,将x→1-转换成t→0+.
(Ⅱ)对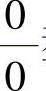 型未定式极限
型未定式极限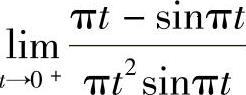 在应用洛必达法则前,先用等价无穷小代替,将未定式极限简化为
在应用洛必达法则前,先用等价无穷小代替,将未定式极限简化为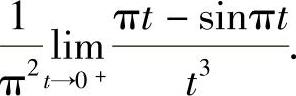
(16)记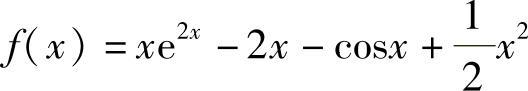 ,则f(x)在[0,1]上连续,且
,则f(x)在[0,1]上连续,且
f′(x)=e2x+2xe2x-2+sinx+x,
f″(x)=4e2x+4xe2x+cosx+1>0 (x∈(0,1)),
所以由f′(0)f′(1)=(-1)×(3e2-1+sin1)<0知,存在唯一的x0∈(0,1),使得
于是f(x)<f(0)=-1<0(x∈[0,x0]),即方程f(x)=0在[0,x0]上无实根.由于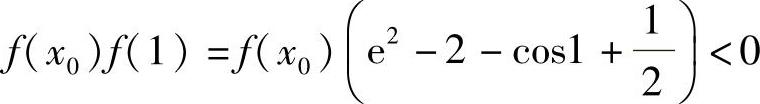 ,且f(x)在(x0,1)内单调增加,所以方程f(x)=0在(x0,1)内有且仅有一个实根.
,且f(x)在(x0,1)内单调增加,所以方程f(x)=0在(x0,1)内有且仅有一个实根.
综上所述,方程f(x)=0在(0,1)内有且仅有一个实根.
附注 由于f′(x)在(0,1)内是变号的,所以不能由f(0)f(1)<0确定方程f(x)=0在(0,1)内有且仅有一个实根.因此需进一步分析,即考虑f″(x).本题就是按此思路求解的.
(17)由φ(x)单调知,它的反函数φ-1(x)存在,于是由φ(x)可导得
从而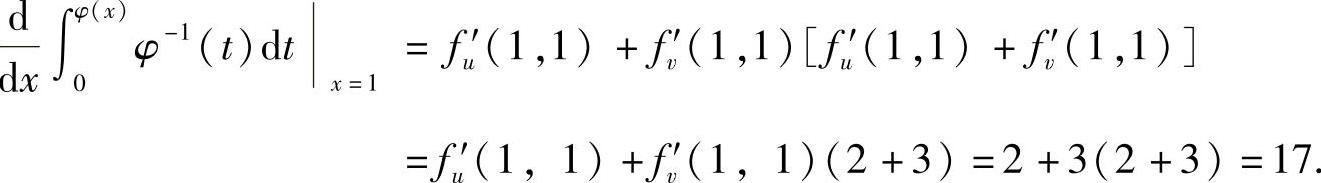
附注 题解中应注意的是:φ-1(φ(x))=x.
(18)由于
所以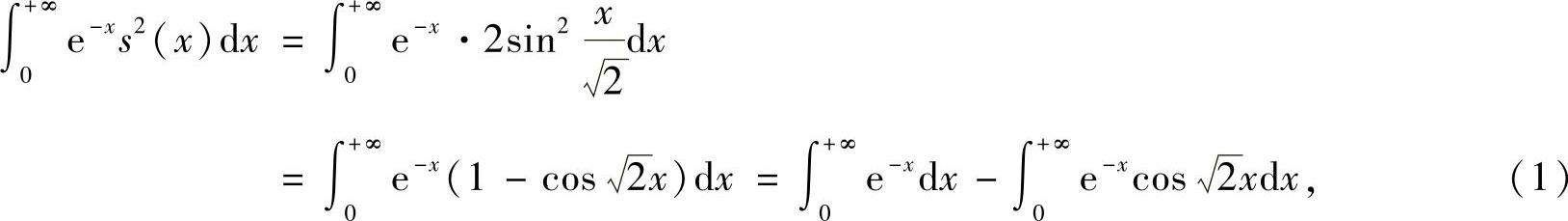 其中,
其中,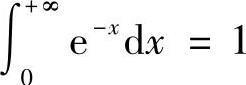 ,此外由
,此外由
得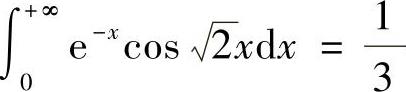 .将以上计算代入式(1)得
.将以上计算代入式(1)得
附注 应记住sinx,cosx的麦克劳林展开式:
本题就是按此公式快捷算得所给幂级数的和函数s(x).
(19)所给微分方程
对应的齐次微分方程的通解为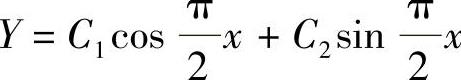 ,此外,式(1)有特解y∗=x,所以式(1)的通解为
,此外,式(1)有特解y∗=x,所以式(1)的通解为
且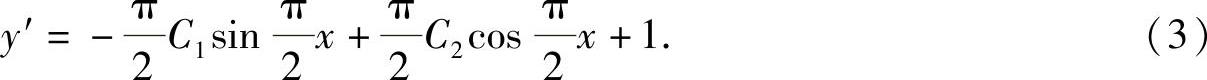
将y(0)=1,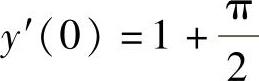 代入式(2),式(3)得C1=C2=1,所以
代入式(2),式(3)得C1=C2=1,所以
下面计算y(x)(-1≤x≤1)的傅里叶级数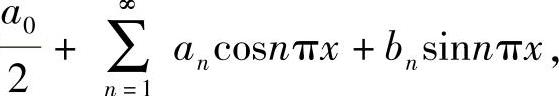
对于n=1,2,…
所以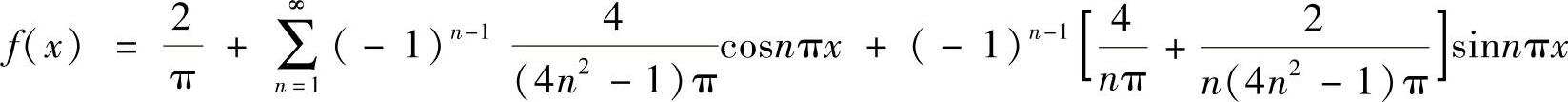 (-1≤x≤1).
(-1≤x≤1).
附注 要熟练掌握函数f(x)(-l≤x≤l)的傅里叶系数的计算.
(20)由A有零特征值知
要使矩阵方程AX=B有解,必须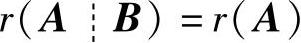 .于是由
.于是由
知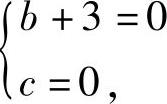 ,即b=-3,c=0.设
,即b=-3,c=0.设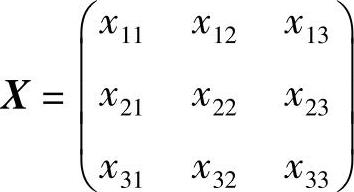 ,并将a=1,b=-3,c=0代入,则矩阵方程AX=B与
,并将a=1,b=-3,c=0代入,则矩阵方程AX=B与
同解,而式(1)即为以下三个线性方程组
显然,式(2)的通解为C1(2,1,-1)T+(2,-1,0)T=(2C1+2,C1-1,-C1)T,
式(3)的通解为C2(2,1,-1)T+(2,0,0)T=(2C2+2,C2,-C2)T,
式(4)的通解为C3(2,1,-1)T+(3,2,0)T=(2C3+3,C3+2,-C3)T,
所以,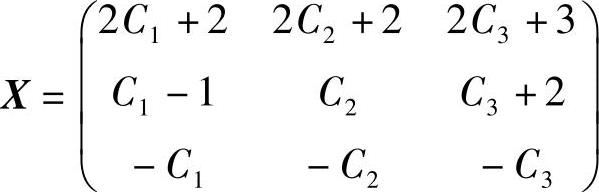 (其中,C1,C2,C3是任意常数).
(其中,C1,C2,C3是任意常数).
附注 矩阵方程AX=B的解法见模拟试题(二)(20)的解答.
(21)(Ⅰ)由于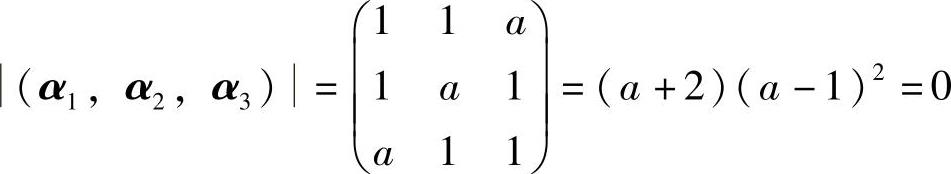 的解为a=1,-2.当a=1时,由
的解为a=1,-2.当a=1时,由
知,β不能由α1,α2,α3线性表示.
当a=-2时,
β=(C+1)α1+Cα2+Cα3 (其中C是任意常数).
(Ⅱ)由于a=-2时,
=λ(λ-3)(λ+3),
所以A有特征值λ=0,3,-3.
设对应λ=0的特征向量为a=(a1,a2,a3)T,则a满足
由于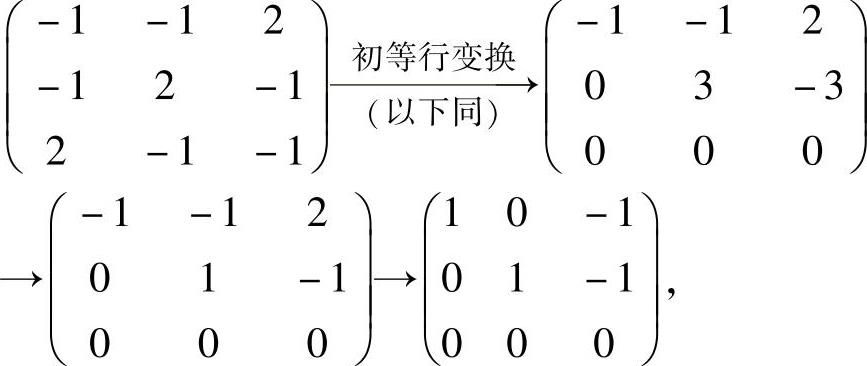
所以式(1)与方程组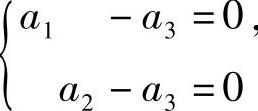
同解,故a可取它的基础解系,即a=(1,1,1)T.
设对应λ=3的特征向量为b=(b1,b2,b3)T,则b满足
由于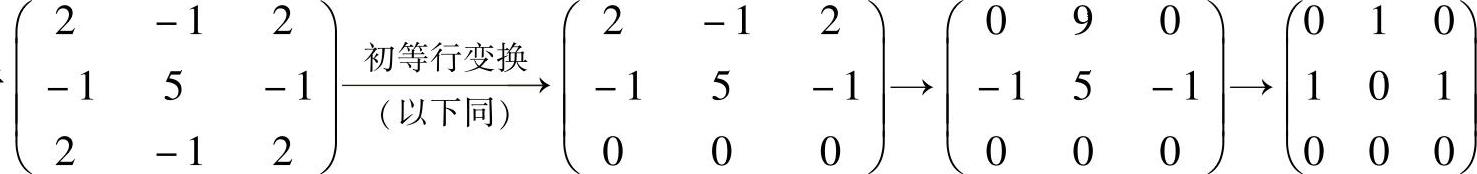 ,所以式
,所以式
(2)与方程组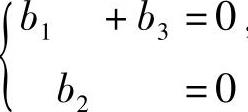
,
同解,故b可取它的基础解系,即b=(1,0,-1)T.设对应λ=-3的特征向量为c=(c1,c2,c3)T,则由A是实对称矩阵知,c与a,b都正交,所以有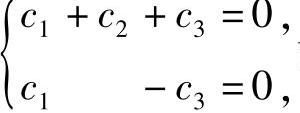 故c可取它的基础解系,即c=(1,-2,1)1.
故c可取它的基础解系,即c=(1,-2,1)1.
a,b,c是正交向量组,现将它们单位化得
记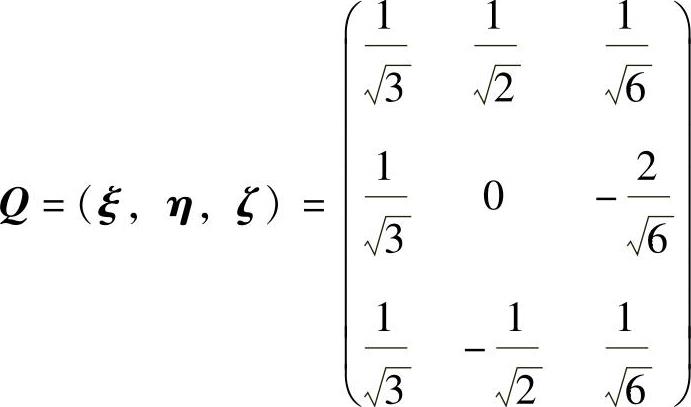 (正交矩阵),则正交变换x=Qy将f(x1,x2,x3)化为标准形3y22-3y23.
(正交矩阵),则正交变换x=Qy将f(x1,x2,x3)化为标准形3y22-3y23.
附注 由于当|(α1,α2,α3)|≠0,即α1,α2,α3线性无关时,β必可由α1,α2,α3唯一线性表示.因此题解从|(α1,α2,α3)|=0入手.
(22)由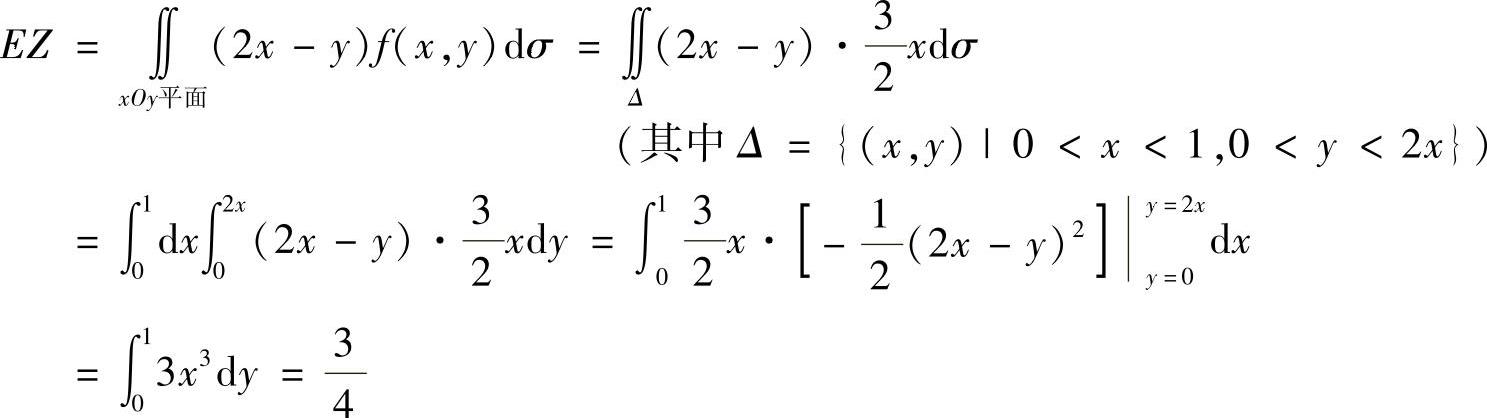
得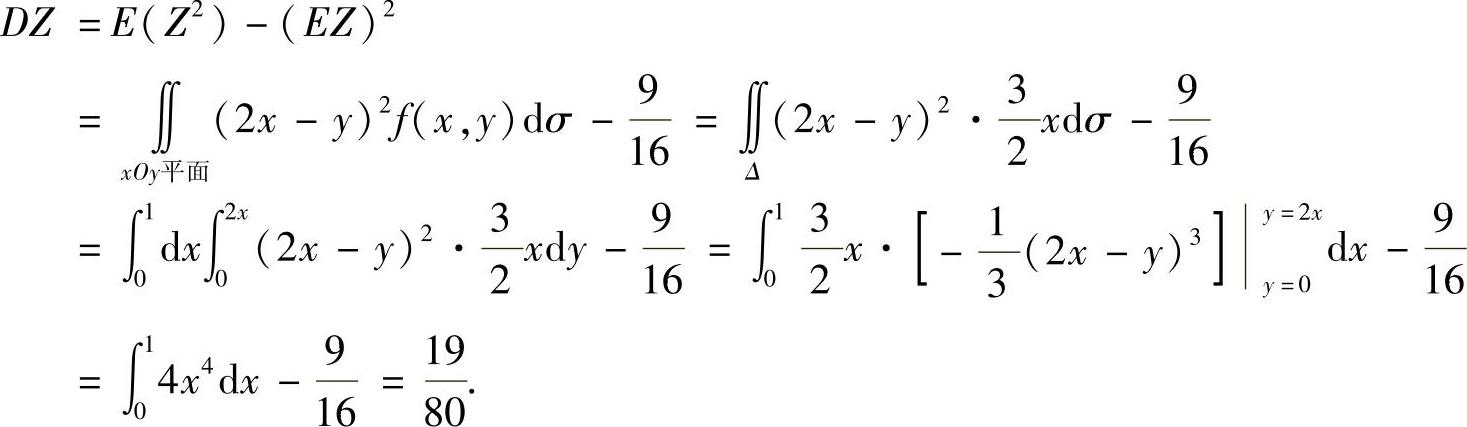
由Z=2X-Y得
其中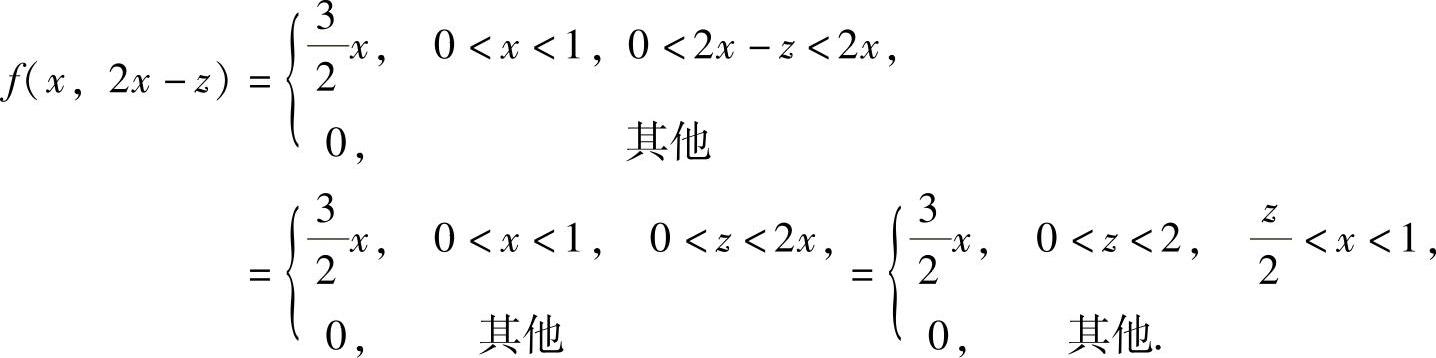
因此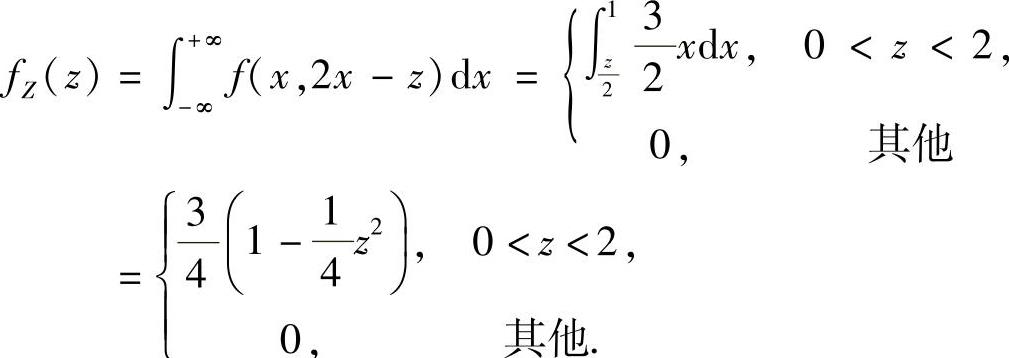
附注 记住以下公式:
设二维随机变量(X,Y)的概率密度为f(x,y),则随机变量Z=aX+bY+c(a,b,c是常数)的概率密度可按以下公式计算:
当a≠0时,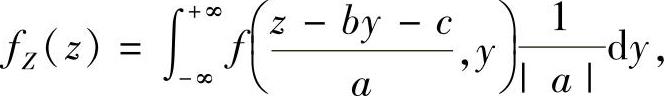
当b≠0时,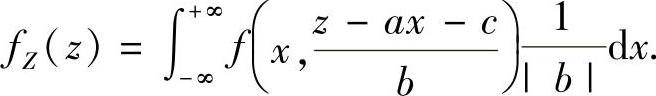
(23)设Z的分布函数为FZ(z),则
所以,Z的概率密度为
即Z~N(0,σ2).于是由矩估计法,令
因此σ2的矩估计量为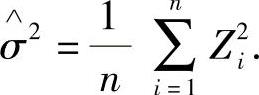
附注 记住以下结论是有用的.
设X1,X2,…,Xn是总体X的简单随机样本,则当X~N(μ,σ2)时,μ的矩估计量为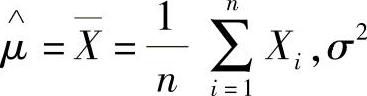 的矩估计量为
的矩估计量为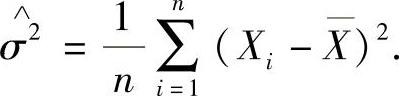 当X~N(0,σ2)时,σ2的矩估计量为
当X~N(0,σ2)时,σ2的矩估计量为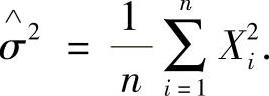
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




