一、选择题
答案
(1)在(-π,0)内f(x)仅有间断点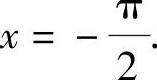 由于
由于
所以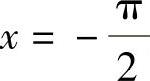 是f(x)的可去间断点.
是f(x)的可去间断点.
在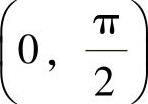 内f(x)无间断点.此外,由于
内f(x)无间断点.此外,由于
所以x=0不是f(x)的可去间断点.
由此可知,f(x)的可去间断点数为1.因此选(B).
附注 寻找分段函数的间断点,除各个分段区间内的间断点外,还应通过考虑函数在分段点处的连续性,确定它是否为间断点.
(2)a=-2,-1时,f(x)在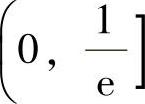 上无定义,所以选项(A),(B)应排除.当a=0时,
上无定义,所以选项(A),(B)应排除.当a=0时,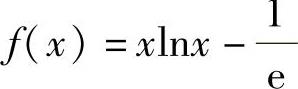 ,且在(0,+∞)上,由
,且在(0,+∞)上,由
知,f(x)的单调减少区间仅为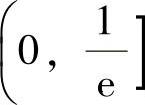 .因此选(C).
.因此选(C).
附注 本题是对选项逐一检验,直到得到正确的选项为止.这是求解单项选择题的常用方法之一.
(3)当x<0时,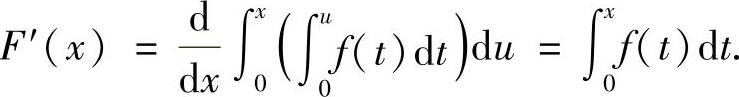
当x>0时,由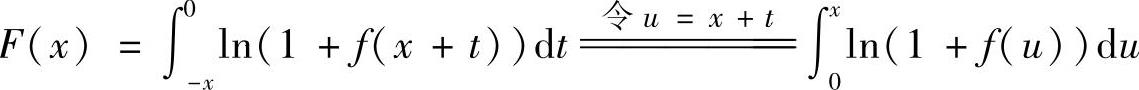
得 F′(x)=ln(1+f(x)).此外,由
知F′(0)=0.所以由
得F″(0)=0.因此选(D).
附注 题解中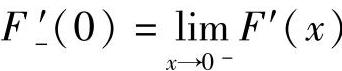 与
与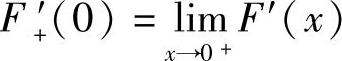 是根据以下结论:
是根据以下结论:
设函数φ(x)在点x=0处连续,在(-δ,0)(δ>0)内可导,且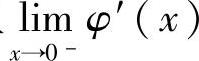 存在,则
存在,则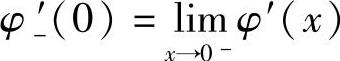 ;
;
设函数ψ(x)在点x=0处连续,在(0,δ)(δ>0)内可导,且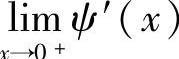 存在,则
存在,则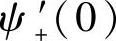
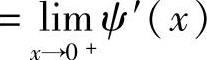 .
.
第二个结论是2009年考研真题,第一个结论的证明与第二个相似.因此上述这些结论都可作为定理用于解题.
(4)由于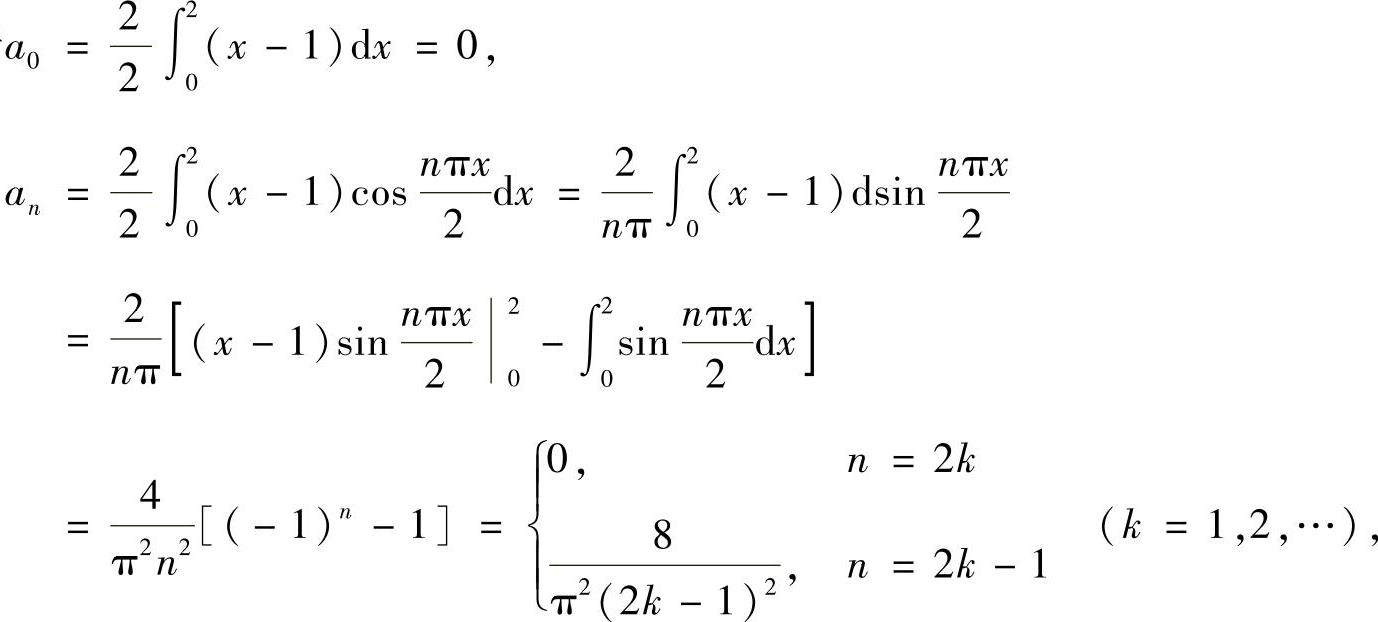
所以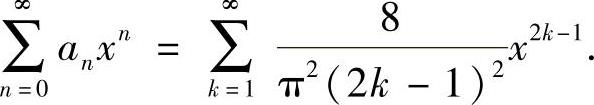
记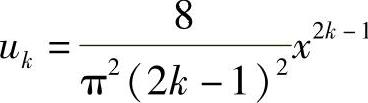 ,则
,则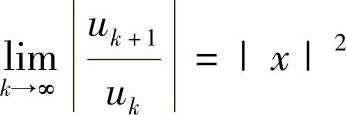 .所以当|x|<1时
.所以当|x|<1时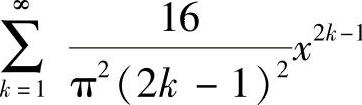 收敛;当|x|>1时,
收敛;当|x|>1时,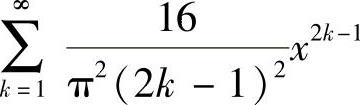 发散.此外,当x=-1,1时,
发散.此外,当x=-1,1时,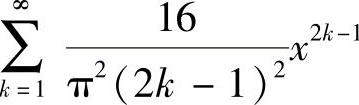 分别成为-
分别成为-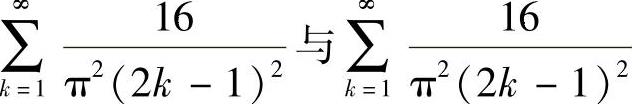 ,它们都是收敛级数.于是
,它们都是收敛级数.于是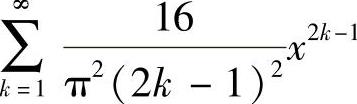 的收敛域为[-1,1],从而
的收敛域为[-1,1],从而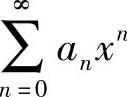 的收敛域为[-1,1],因此选(D).
的收敛域为[-1,1],因此选(D).
附注 缺项幂级数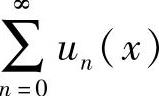 的收敛域可按以下步骤计算:
的收敛域可按以下步骤计算:
第一步计算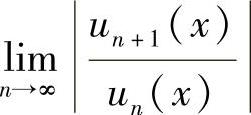 ,设其为A(x);
,设其为A(x);
第二步解不等式A(x)<1,设其解为-a<x<a;
第三步考虑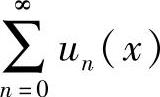 在点x=-a,a处的收敛性,则
在点x=-a,a处的收敛性,则 的收敛域为(-a,a)与收敛的端点的并集.
的收敛域为(-a,a)与收敛的端点的并集.
(5)由(A∗)T=(AT)∗=(-A)∗=(-1)n-1A∗知,n为奇数时,有(A∗)T=A∗.即A∗是对称矩阵.反之,当A∗是对称矩阵,即(A∗)T=A∗时,由以上计算得(-1)n-1=1,即n为奇数.
所以A∗为对称矩阵是n为奇数的充分必要条件,因此选(C).
附注 对于n(n≥2)阶矩阵A,A∗=O的充分必要条件是r(A)<n-1.因此A∗≠O的充分必要条件是r(A)=n或n-1.
(6)由于A~B,所以存在3阶可逆矩阵P,使得
P-1AP=B.
于是,r(A-2E3)=r(P-1(A-2E3)P)=r(B-2E3).由于
所以r(A-2E3)=r(B-2E3)=3.
所以,r(A-E3)=r(B-E3)=2.
从而r(A-2E3)+r(A-E3)=5.因此选(D).
附注 本题也可按以下方法计算:
其中 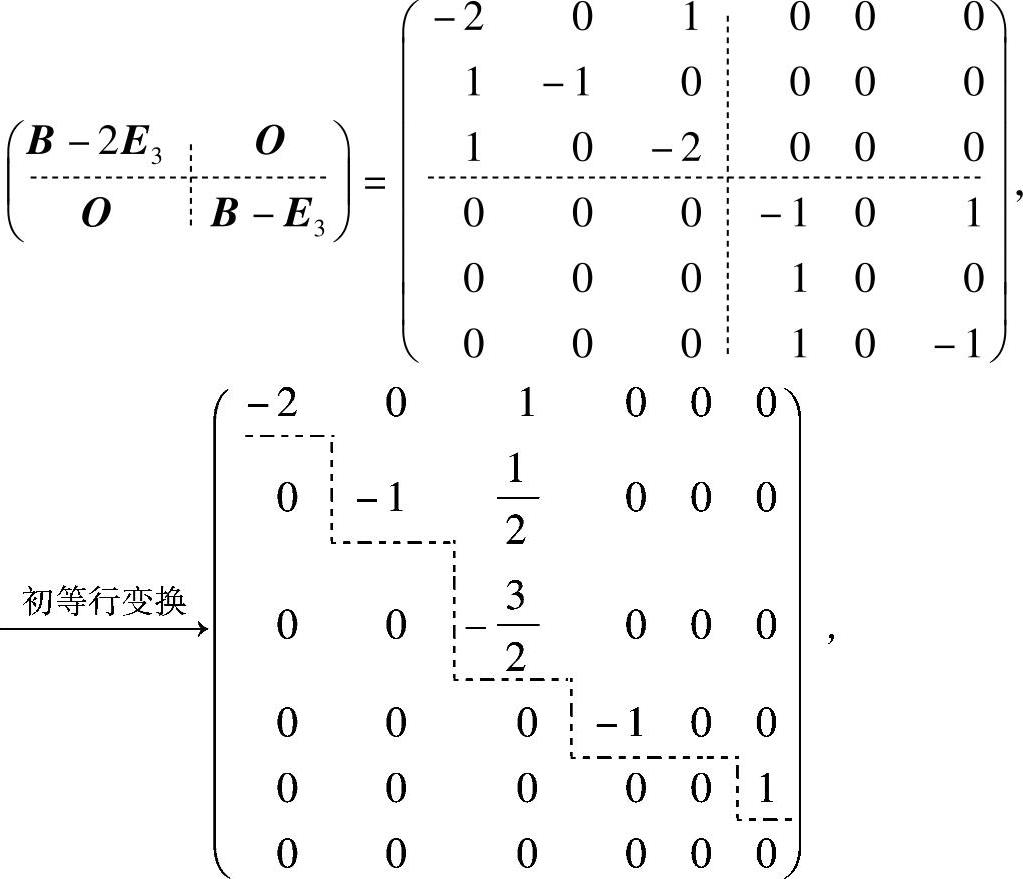
所以,r(A-2E3)+r(A-E3)=5.
(7)由关于X的边缘分布函数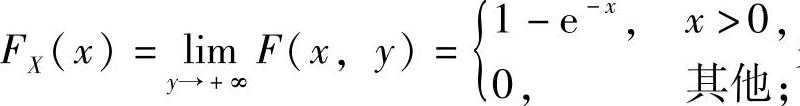 关于Y的边缘分布函数
关于Y的边缘分布函数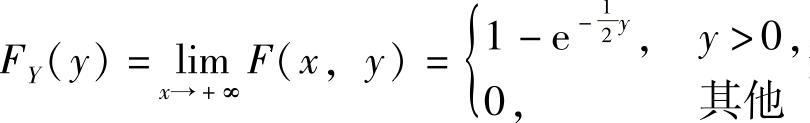 知F(x,y)=FX(x)FY(y)(-∞<x<+∞,-∞<y<+∞),所以X与Y相互独立,从而
知F(x,y)=FX(x)FY(y)(-∞<x<+∞,-∞<y<+∞),所以X与Y相互独立,从而
由此可知选项(C)不正确.因此选(C).
附注 题解中,实际上已给出选项(A),(D)都正确.选项(B)也是正确的,这是因为关于Y的边缘概率密度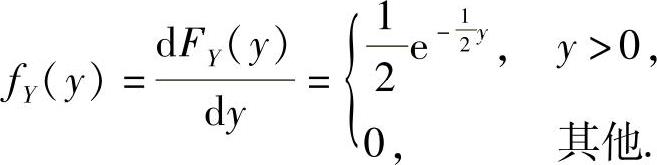 所以EY=2.
所以EY=2.
(8)由题设知,X1,X2,X3,X4相互独立,且
E(X1-2X2)=0,D(X1-2X2)=D(X1)+4D(X2)=20,
E(3X3-4X4)=0,D(3X3-4X4)=9D(X3)+16D(X4)=100.
于是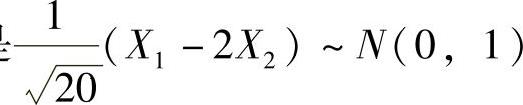 ,
,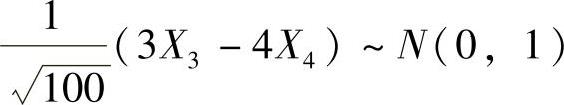 ,且它们相互独立,所以,
,且它们相互独立,所以,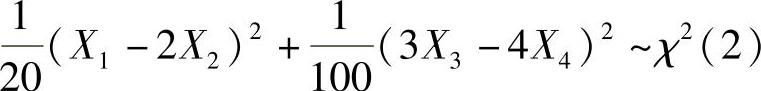 .从而D(Z)=4.因此选(A).
.从而D(Z)=4.因此选(A).
附注 设X1,X2,…,Xn是来自总体X~N(μ,σ2)的简单随机样本,则
其中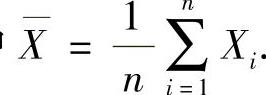
二、填空题
(9)由于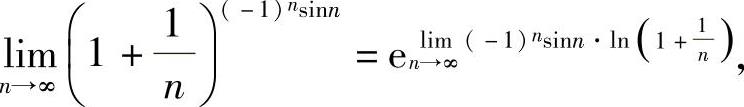
其中,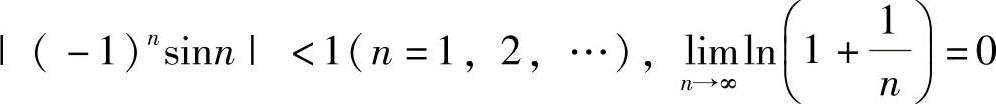 ,所以
,所以
附注 设α(x)是有界函数,β(x)是某个极限过程中的无穷小,则在这个极限过程中有
limα(x)β(x)=0.
(10)由于x∈[-1,1]时,ψ(x)=(x-1)2,显然x∈[-1,0)时,ψ(x)>1;x∈[0,1]时,ψ(x)≤1,所以
于是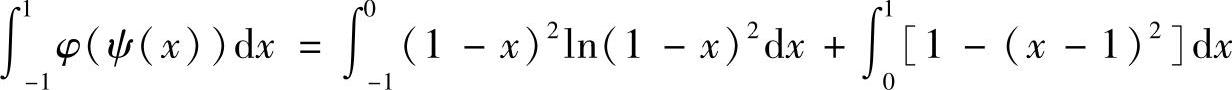 ,其中
,其中
所以,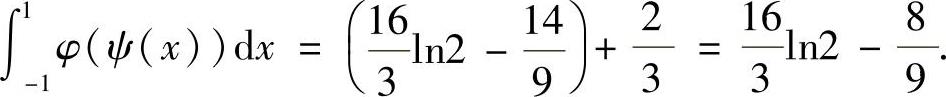
附注 平时应练习分段函数的复合运算.
(11)由题设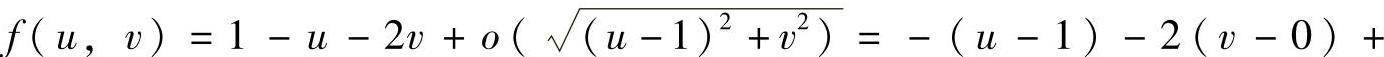
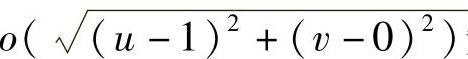 知
知
f(1,0)=0,f′u(1,0)=-1,f′v(1,0)=-2.
记u=ey,v=x+y,则g(x,y)=f(u,v),且
g′x(x,y)=f′v(u,v),g′y(x,y)=f′u(u,v)ey+f′v(u,v).所以dg(x,y)(0,0)=g′x(0,0)dx+g′y(0,0)dy=f′v(1,0)dx+[f′u(1,0)+f′v(1,0)]dy=-2dx-3dy.
附注 本题获解的关键是由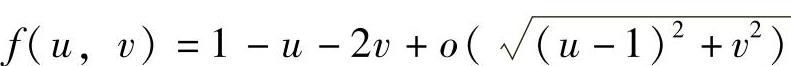 得到f′u(1,0)=-1,f′v(1,0)=-2.
得到f′u(1,0)=-1,f′v(1,0)=-2.
(12)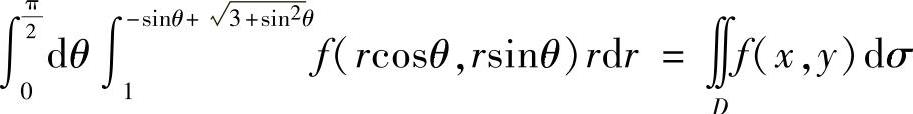 ,其中
,其中
D是由曲线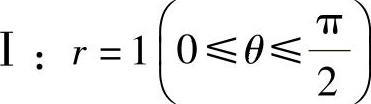 ,Ⅱ:
,Ⅱ: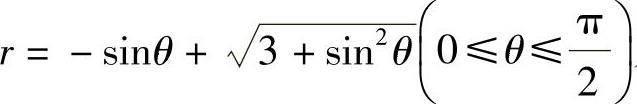 及Ⅲ:θ=0围成.
及Ⅲ:θ=0围成.
显然Ⅰ的方程为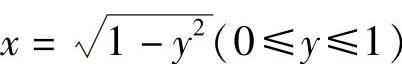 .由于Ⅱ的方程可改写成
.由于Ⅱ的方程可改写成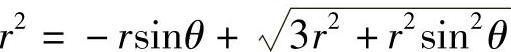 ,即x
,即x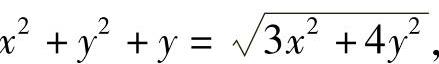 或者,
或者,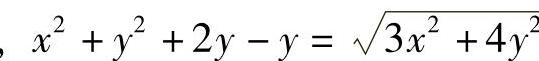 ,两边平方后得
,两边平方后得
(x2+y2+2y)2-(2y+3)(x2+y2+2y)+3·2y=0,
即(x2+y2)(x2+y2+2y-3)=0.由此得到Ⅱ的方程为x2+y2+2y=3,即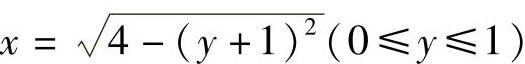 .Ⅲ的方程为y=0.于是D如图答3-12阴影部分所示,所以有
.Ⅲ的方程为y=0.于是D如图答3-12阴影部分所示,所以有
上式右边即为所求的先x后y的二次积分.
图答 3-12
附注 对某个二次积分I,要改变它的积分次序或积分坐标系,总是先写出与I相对应的二重积分,然后再将这个二重积分转化为所要求的二次积分.
(13)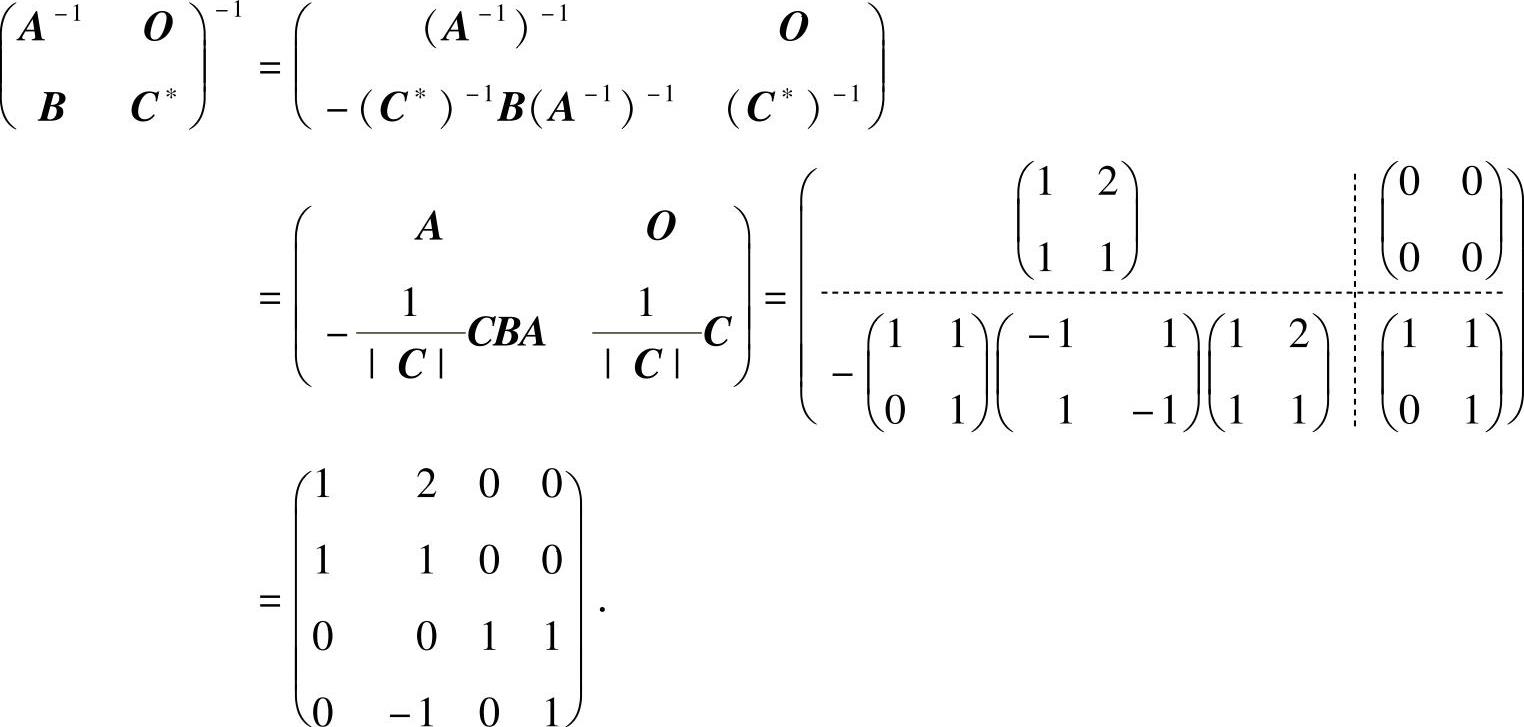
附注 这里利用了分块矩阵的求逆公式:
设A,D都是可逆矩阵,则
同样有,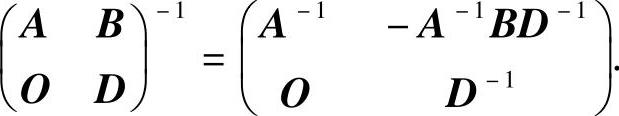
(14)由题设知P(A)=P(B),于是由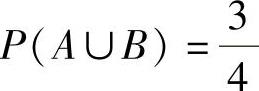 得
得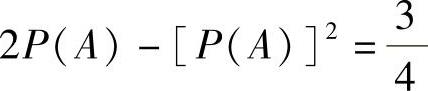 ,即
,即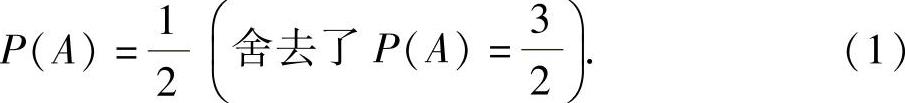 由此可知0<a<2(这是因为,如果a≤0,则P(A)=1,这与
由此可知0<a<2(这是因为,如果a≤0,则P(A)=1,这与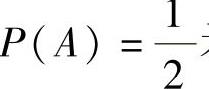 矛盾;如果a≥2,则P(A)=0,这也与
矛盾;如果a≥2,则P(A)=0,这也与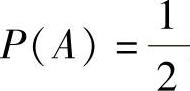 矛盾).于是由式(1)得
矛盾).于是由式(1)得
附注 根据题设推出P(A)=P(B)以及0<a<2是本题获解的关键.
三、解答题
(15)所给微分方程y″+a2y=sinx+2cos2x(1)对应的齐次方程的通解为
Y=C1cosax+C2sinax(C1,C2是任意常数).
当a=1时,式(1)有特解
y∗=x(A1sinx+B1cosx)+(A2sin2x+B2cos2x).(https://www.xing528.com)
将它代入a=1时的式(1)得
2A1cosx-2B1sinx-3A2sin2x-3B2cos2x=sinx+2cos2x.
由此得到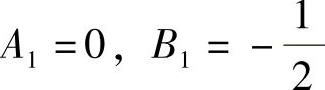 ,A2=0,
,A2=0,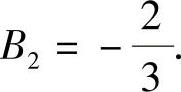 故
故
因此,当a=1时,式(1)的通解为
当a=2时,式(1)有特解
y∗=A1sinx+B1cosx+x(A2cos2x+B2sin2x).
代入a=2时的式(1)得
3A1sinx+3B1cosx-4A2sin2x+4B2cos2x=sinx+2cos2x.
由此得到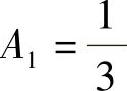 ,B1=0,A2=0,
,B1=0,A2=0,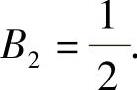 故
故
因此,当a=2时,式(1)的通解为
附注 设有2阶线性微分方程
y″+ay′+by=eαx(a1cosβx+b1sinβx)(∗)
(其中a,b,a1,b1,α,β都是常数),则式(∗)有特解
y∗=xkeαx(Acosβx+Bsinβx),
其中 常数A,B可由y∗代入式(∗)确定.
常数A,B可由y∗代入式(∗)确定.
(16)由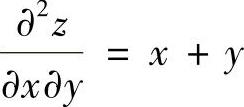 得
得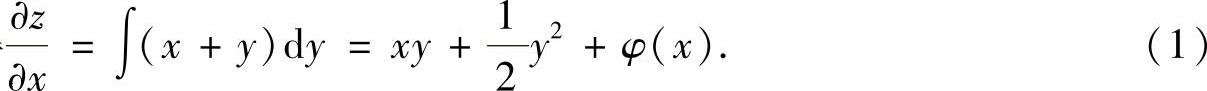
z(x,0)=x两边对x求偏导数得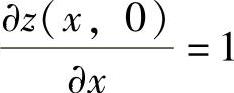 ,将它与由式(1)得到的
,将它与由式(1)得到的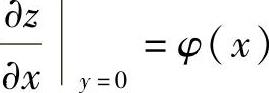 比较得φ(x)=1,所以
比较得φ(x)=1,所以
由此得到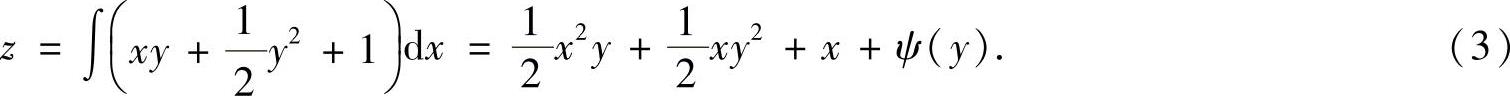
式(3)中令x=0,则由z(0,y)=y2得ψ(y)=y2.代入式(3)得
由式(2)得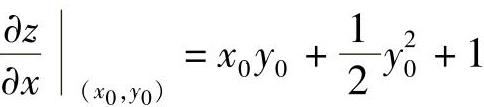 ,由式(4)得
,由式(4)得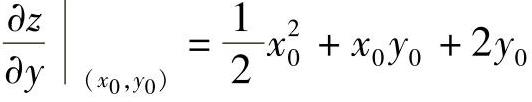 .于是由曲面S:z=z(x,y)(x>0)的在点(x0,y0,z0)处的切平面与π平行得
.于是由曲面S:z=z(x,y)(x>0)的在点(x0,y0,z0)处的切平面与π平行得
解此方程组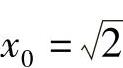 ,y0=0代入式(4)得
,y0=0代入式(4)得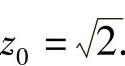 因此所求的点
因此所求的点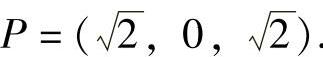
附注 题解中应注意的是:
由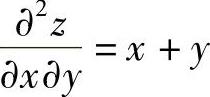 得
得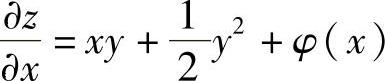 ,而不是
,而不是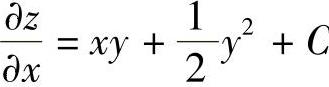 .同样,由
.同样,由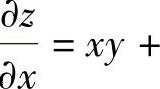
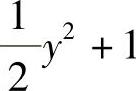 得
得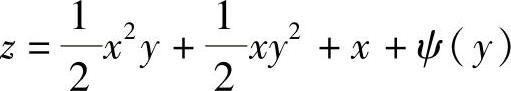 ,而不是
,而不是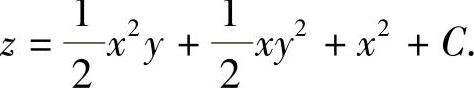 上述的C都为任意常数.
上述的C都为任意常数.
(17)由于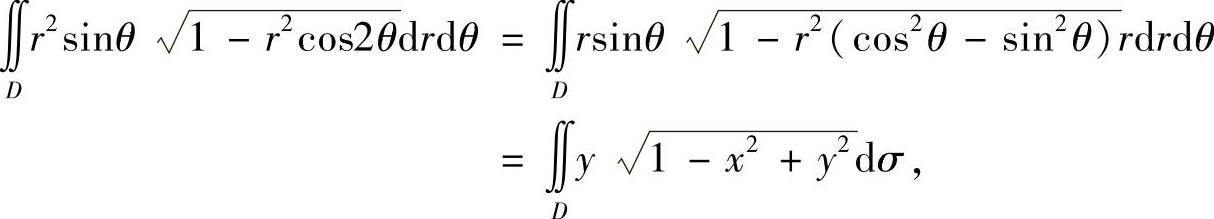
所以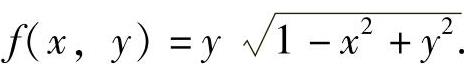 此外
此外
如图答3-17阴影部分所示.由于
图答 3-17
所以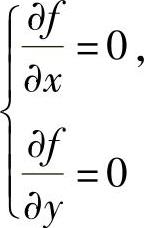 在D的内部无解,即f(x,y)在D的内部无可能极值点.
在D的内部无解,即f(x,y)在D的内部无可能极值点.
D有边界Ⅰ:y=0(0≤x≤1),Ⅱ:x=1(0≤y≤1)以及Ⅲ:y=x(0≤x≤1).
在Ⅰ上,f(x,y)≡0(0≤x≤1),所以它的最大值与最小值都为0.
在Ⅱ上,f(x,y)=y2(0≤y≤1),所以它的最大值为1,最小值为0.
在Ⅲ上,f(x,y)=x(0≤x≤1),所以它的最大值为1,最小值为0.
因此f(x,y)在D的边界上,即在D上的最大值为1,最小值为0.
附注 题解时应注意的是,f(x,y)在极坐标系中的表达式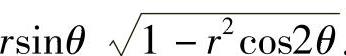 ,而不是
,而不是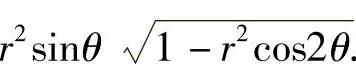
(18)Ω的侧面方程为x2+y2-(z-1)2=1,所以
其中Dz={(x,y)|x2+y2≤1+(z-1)2}是Ω的水平截面(其立坐标z)在xOy平面的投影.
所以
附注 Ω的水平截面是圆,所以对三重积分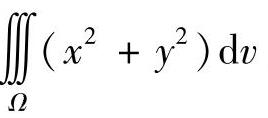 用“先二后一”的方法计算.
用“先二后一”的方法计算.
(19)记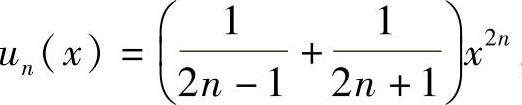 ,则
,则
所以,所给幂级数在|x|<1时收敛,|x|>1时发散,此外,在x=-1,1时,所给幂级数都成为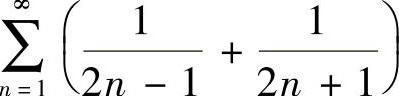 ,它是发散级数.
,它是发散级数.
因此,所给幂级数的收敛域为(-1,1).
由于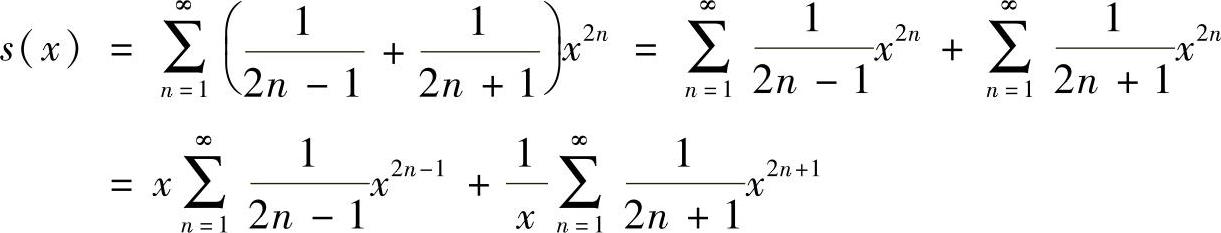
且s(0)=0,所以,
附注 本题利用以下公式,快捷地算得幂级数的和函数:
(20)(Ⅰ)由(A)与(B)等价知,r(β1,β2,β3)=r(α1,α2,α3).由于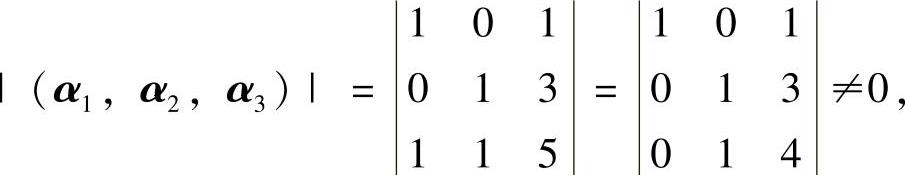 即r(α1,α2,α3)=3,所以r(β1,β2,β3)=3,即
即r(α1,α2,α3)=3,所以r(β1,β2,β3)=3,即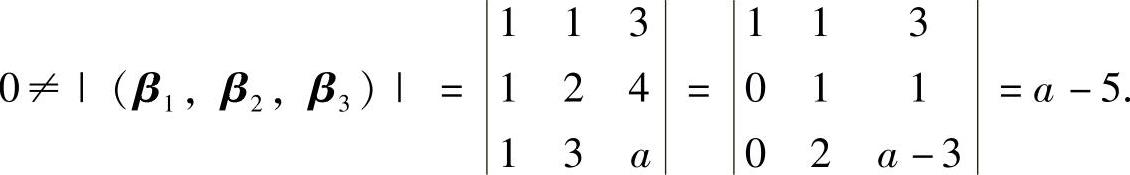 由此得到a≠5.
由此得到a≠5.
(Ⅱ)当a≠5时,由
知,(A)由(B)的线性表示式为
附注 将初等行变换后的矩阵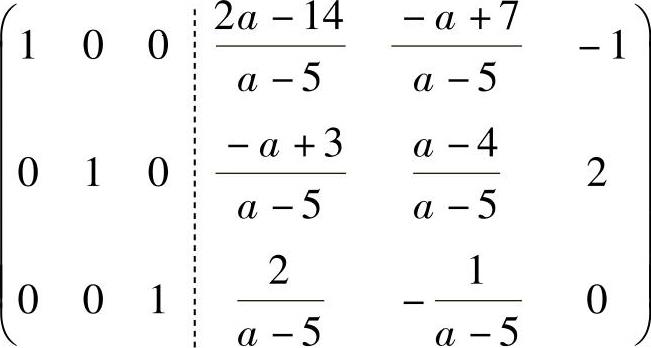 的列向量由左至右顺序记为β′1,β′2,β′3;α′1,α′2,α′3,容易看到
的列向量由左至右顺序记为β′1,β′2,β′3;α′1,α′2,α′3,容易看到
由于“初等行变换不改变列向量之间的线性表示关系”(记住这一结论),因此由式(2)直接得到式(1),即(A)由(B)线性表示式.
(A)由(B)的线性表示式也可以用以下方法计算:
记 e1=(1,0,0)T,e2=(0,1,0)T,e3=(0,0,1)T,则由
得
于是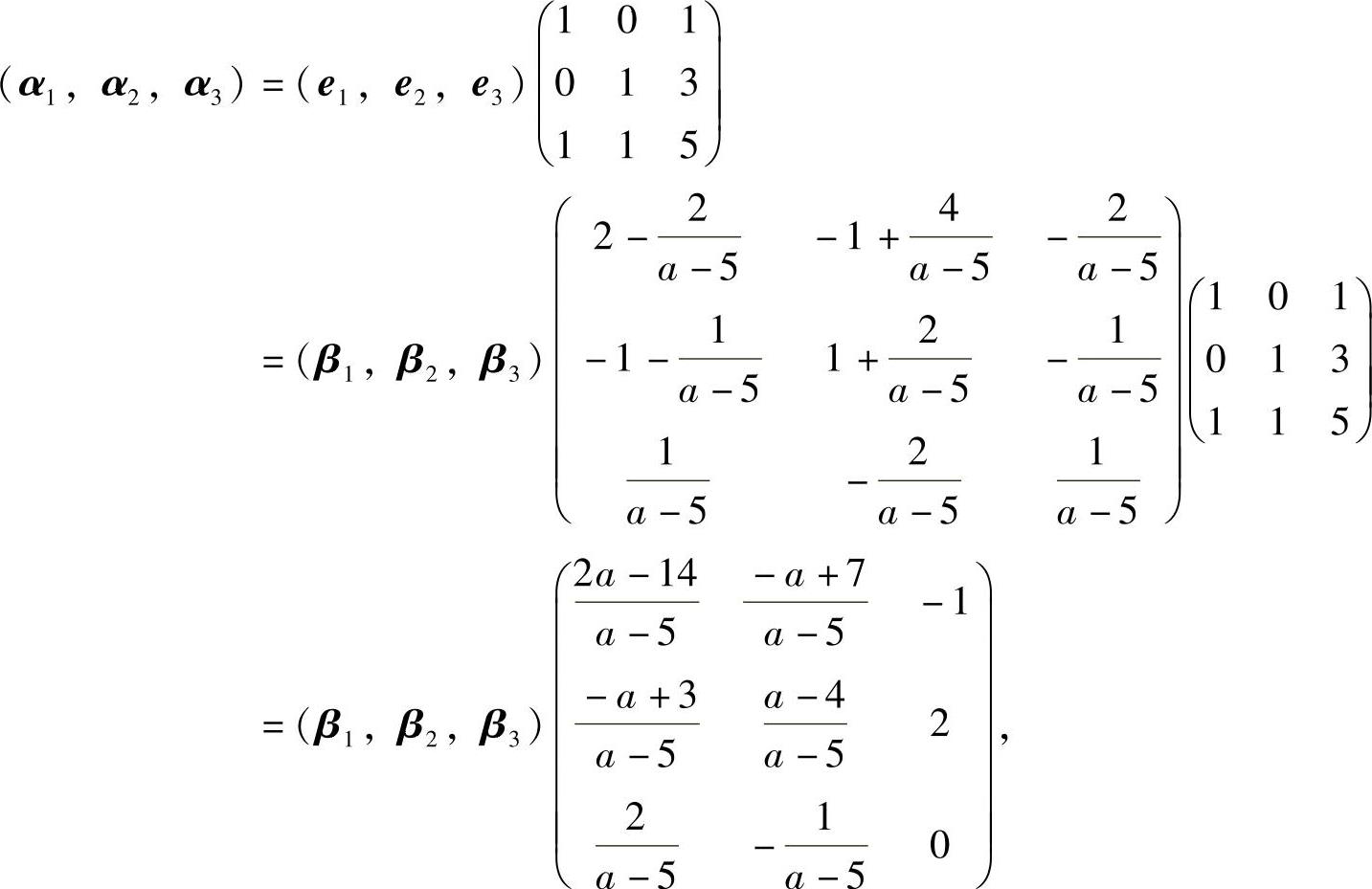
它即为式(1).
(21)(Ⅰ)由于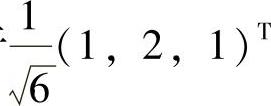 是A的一个特征向量,记它对应的特征值为λ,则有
是A的一个特征向量,记它对应的特征值为λ,则有
解此方程组得λ=2,a=-1.
将a=-1代入A,得A的特征方程
它的根除λ1=λ=2外,还有λ2=5,λ3=-4,所以,f(x1,x2,x3)的标准形为2y21+5y22-4y23.
由于A∗是实对称矩阵,所以它能化为对角矩阵Λ.由于A∗的特征值为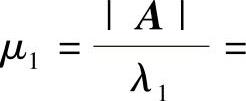
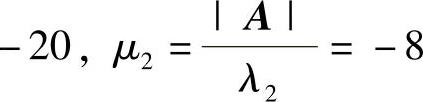 ,
,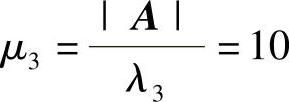 ,所以
,所以
由题设知,A的对应λ1=2的特征向量为ξ1=(1,2,1)T.设对应λ2=5的特征向量为ξ2=(u1,u2,u3)T,则
由于 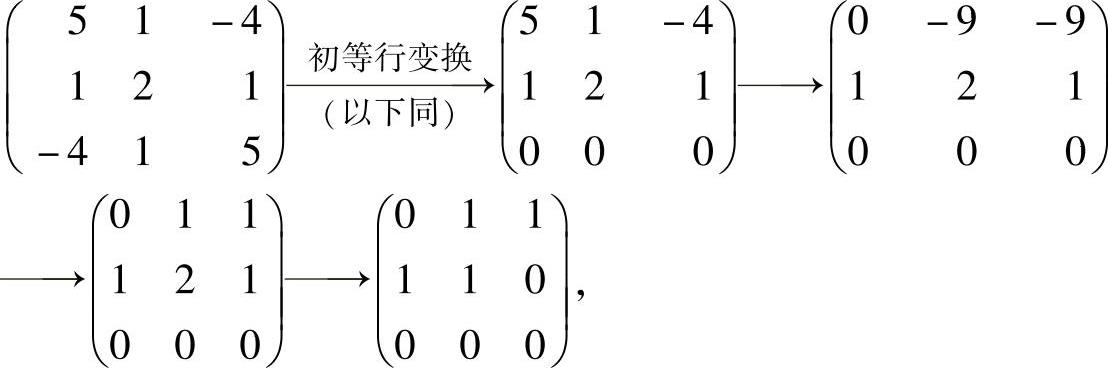
所以,式(1)与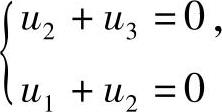 同解,它的基础解系为(1,-1,1)T,故取ξ2=(1,-1,1)T.设对应λ3=-4的特征向量为ξ3=(v1,v2,v3)T,则由A是实对称矩阵知,
同解,它的基础解系为(1,-1,1)T,故取ξ2=(1,-1,1)T.设对应λ3=-4的特征向量为ξ3=(v1,v2,v3)T,则由A是实对称矩阵知,
它的基础解系为(1,0,-1)T,故取ξ3=(1,0,-1)T.显然,ξ1,ξ2,ξ3是正交向量组.现将其单位化得
记P=(ξ01,ξ02,ξ03),则P即为所求的正交矩阵.
附注 设A是可逆实对称矩阵,且有特征值λ及与之对应的特征向量ξ,则A∗有特征值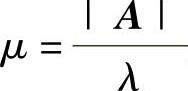 及对应的特征向量ξ.所以当PTAP为对角矩阵时,PTA∗P也是对角矩阵,且对角线上的元素都是A∗的特征值.
及对应的特征向量ξ.所以当PTAP为对角矩阵时,PTA∗P也是对角矩阵,且对角线上的元素都是A∗的特征值.
(22)由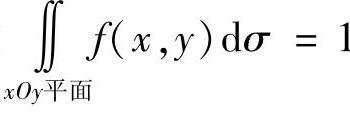 ,即
,即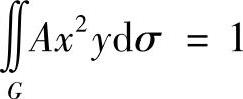 得
得
所以,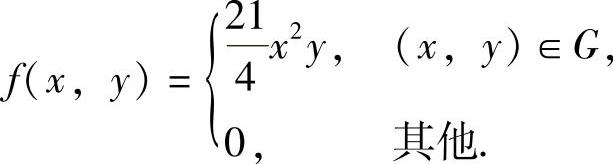
其中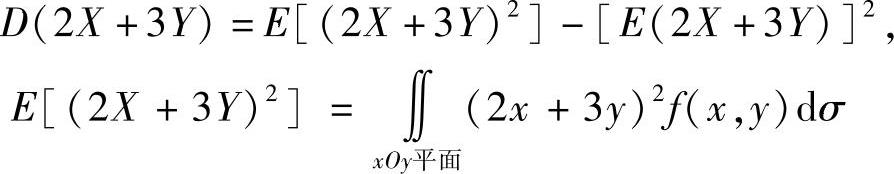
于是,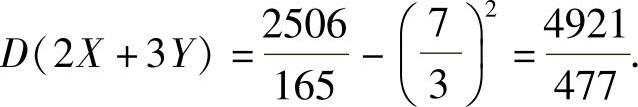
附注 应记住随机变量X的方差计算公式:
DX=E(X2)-(EX)2
(23)由于X的概率密度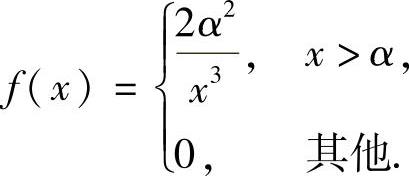 记z=x2,则它在f(x)≠0的区间(α,+∞)上单调增加,反函数x=h(z)=z(z>α2),于是Z的概率密度为
记z=x2,则它在f(x)≠0的区间(α,+∞)上单调增加,反函数x=h(z)=z(z>α2),于是Z的概率密度为
记样本观察值为z1,z2,…,zn(由于现在是计算最大似然估计量,可认为它们都大于α2),故有似然函数为
由于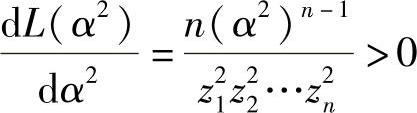 ,所以α2的最大似然估计值为min{z1,z2,…,zn}.从而α2的最大似然计量为
,所以α2的最大似然估计值为min{z1,z2,…,zn}.从而α2的最大似然计量为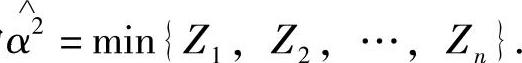
由最大似然值估计量的不变性得α的最大似然估计量为
附注 本题也可计算如下:
由于X的概率密度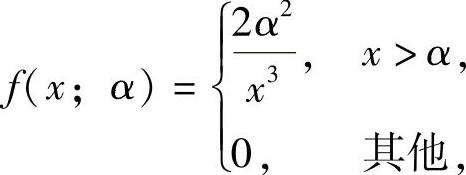 且X有简单随机样本值
且X有简单随机样本值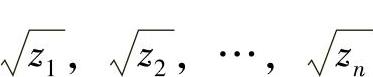 (它们都大于α),所以有似然函数
(它们都大于α),所以有似然函数
于是由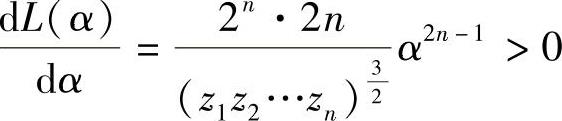 知,α的最大似然估计值为
知,α的最大似然估计值为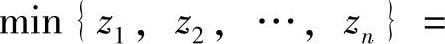
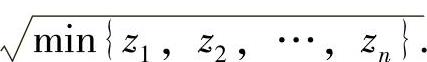 所以α的最大似然估计量
所以α的最大似然估计量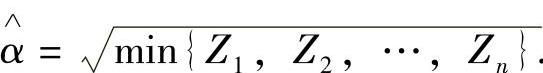
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




