2016考研数学（一）名师精选.全真模拟冲刺题解答

一、选择题

答案

（1）由于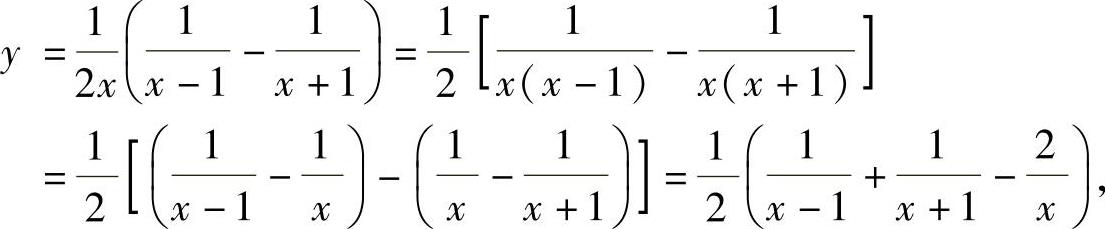

所以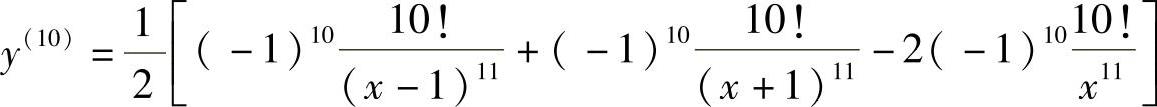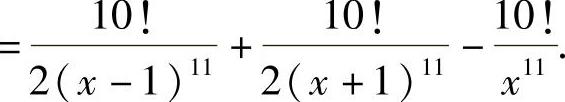， 因此选（C）.

附注 应记住公式：对于a≠0，

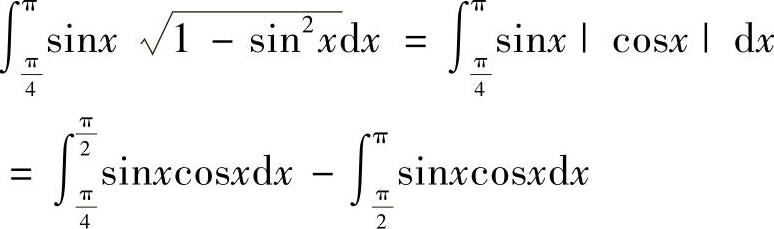
（2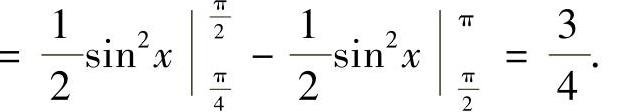） 因此选（A）.

附注 题解中应注意的是：在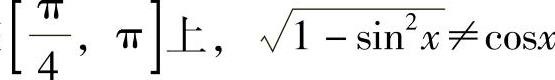，而应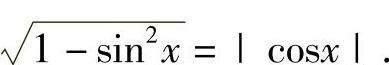

（3）由于x轴负向的方向余弦为（cosπ，sinπ），所以方向导数为

因此选（D）.

附注 由于f（x，y）的偏导数仅在点（0，0）处存在，所以选项（A），（B）及（C）都未必正确.

（4）由于f（x）的余弦级数是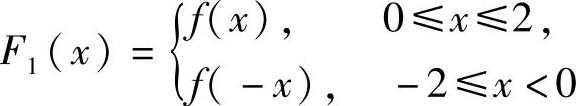的傅里叶级数，所以它的和函数s₁（x）是以4为周期的，于是

由于f（x）的正弦级数是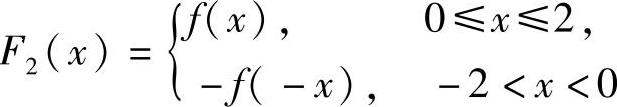的傅里叶级数，所以它的和函数s₂（x）是以4为周期的，于是

由此得到s₁（-3）+s₂（6）=0.因此选（B）.

附注 应记住：计算f（x）（0≤x≤a）的余弦级数（正弦级数）时，应将f（x）作偶延拓（奇延拓），即考虑函数

（5）对于n＞2有

因此选（C）.

附注 当A不可逆时，本题结论仍成立.这是因为，当A不可逆，即|A|=0时，|A|^n-2A=O.另一方面，当|A|=O时，有r（A^∗）=1或0，即r（A^∗）＜n-1从而r（（A^∗）^∗）=0.由此得到（A^∗）^∗=O.故仍有

（A^∗）^∗=|A|^n-2A.

（6）由A是正定矩阵知A是实对称矩阵，故A∗也是实矩阵，并且，由A^T=A得（A^∗）^T=（A^T）^∗=A^∗，所以A^∗也是对称的，从而A∗也是实对称矩阵.此外由A的特征值λ₁，λ₂，…，λ_n全为正的知，A^∗的特征值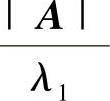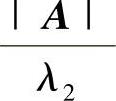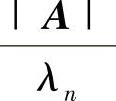，，…，也全为正的.因此A^∗是正定矩阵.同样可得B^∗是正定矩阵.

于是对于任意x（n维非零列向量），有x^TA^∗x＞0，x^TB^∗x＞0，由此可知

x^T（A^∗+2B^∗）x＞0，即A^∗+2B^∗是正定矩阵.因此选（A）.

附注 应记住以下结论：

设A，B都是n阶正定矩阵，则A+B，A^T+B^T，A^-1+B^-1，A^∗+B^∗都是正定矩阵，但A-B，AB，A^TB^T，A^-1B^-1，A^∗B^∗未必是正定矩阵.

（7）由题设知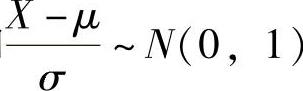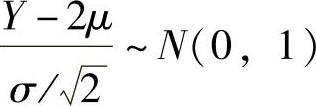，，所以

故有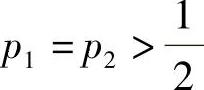.因此选（D）.

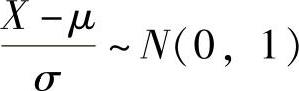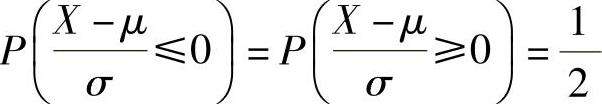附注 由知.所以有

（8）由于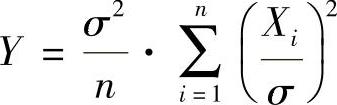，其中由X₁，X₂，…，X_n相互独立，且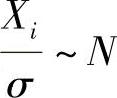（0，1）（i=1，2，…，n）知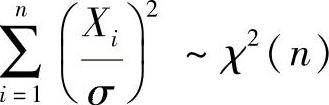，，所以

因此选（C）.

附注 应记住以下结论：

设ξ₁，ξ₂，…，ξ_n是相互独立且都服从N（0，1）的随机变量，则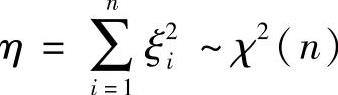，且Eη=n，Dη=2n.

二、填空题

（9）

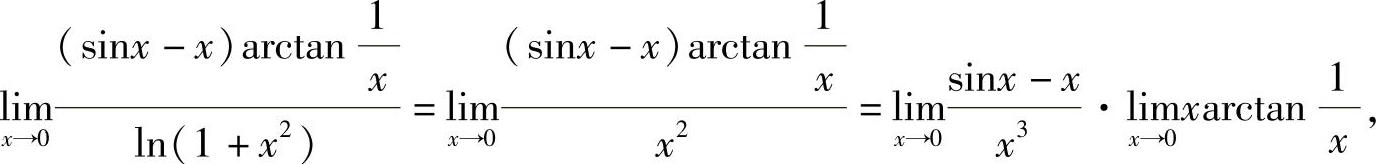
其中，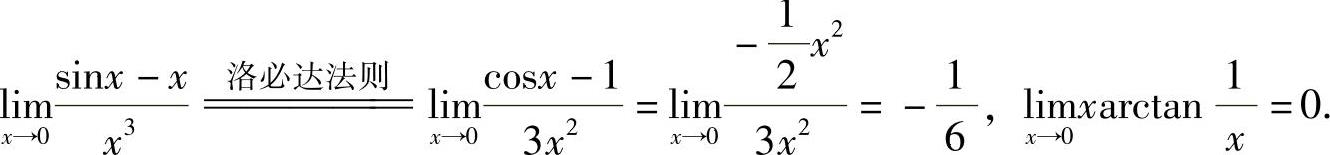

所以，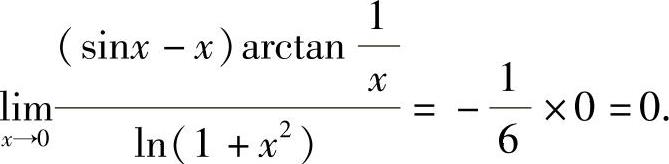

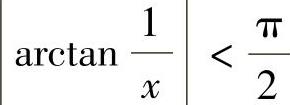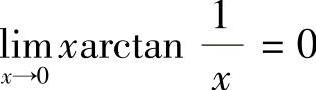附注 由x→0时，x是无穷小，，所以.类似地有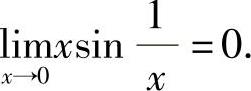

（10）

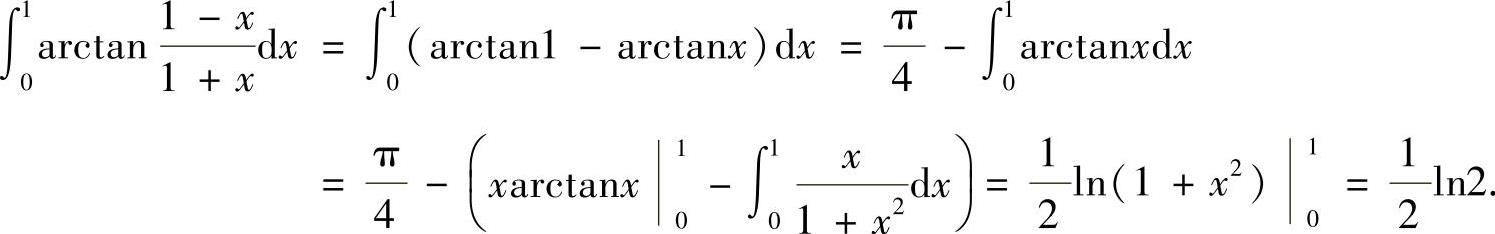
附注 应记住初等数学公式：

（11）由于z_x′（2，1）=2，z_y′（2，1）=2，所以π的方程为

2（x-2）+2（y-1）-（z-2）=0，即2x+2y-z-4=0.因此点（0，0，0）到π的距离

附注 在平面上，点（x₀，y₀）到直线ax+by+c=0的距离为

在空间中，点（x₀，y₀，z₀）到平面Ax+By+Cz+D=0的距离为

（12）记平面z=-3被曲面S截下部分为S₁（下侧），则

所以，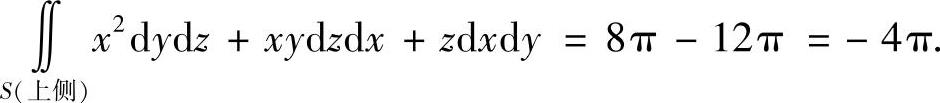

附注 由于S不是闭曲线，所以需添一块S₁，使得S与S₁组成闭曲面（而且方向为外侧）后，才可以应用高斯公式，这是计算关于坐标的曲面积分的常用方法.

（13）由于

所以r（A²）=3，从而r[（A²）^∗]=1.

附注 本题是利用以下公式（应记住）计算的：

设A是n阶矩阵，则

（14）F_Y（y）=P（Y≤y）=P（X²≤y），

其中，y≤0时，P（X²≤y）=0；

y＞0时，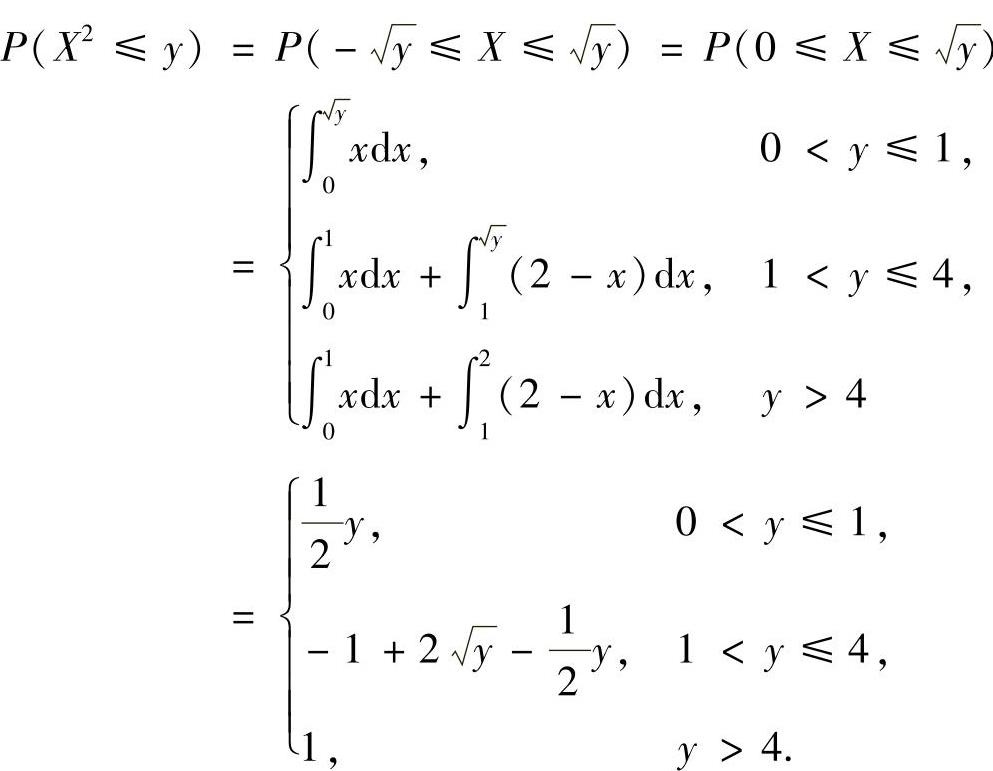

所以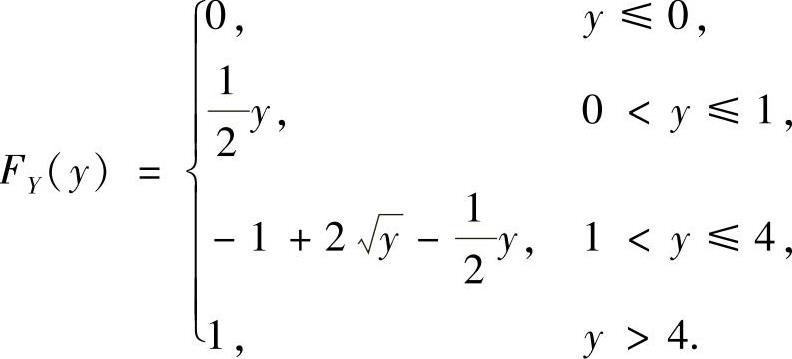

附注 F_Y（y）也可以按以下方法计算：

记g（x）=x²，则g（x）在{x|f（x）≠0}=（0，2）内单调增加，记它的反函数为x=h（y），则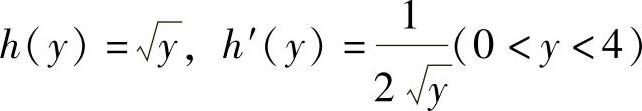.所以

Y的概率密度f

因此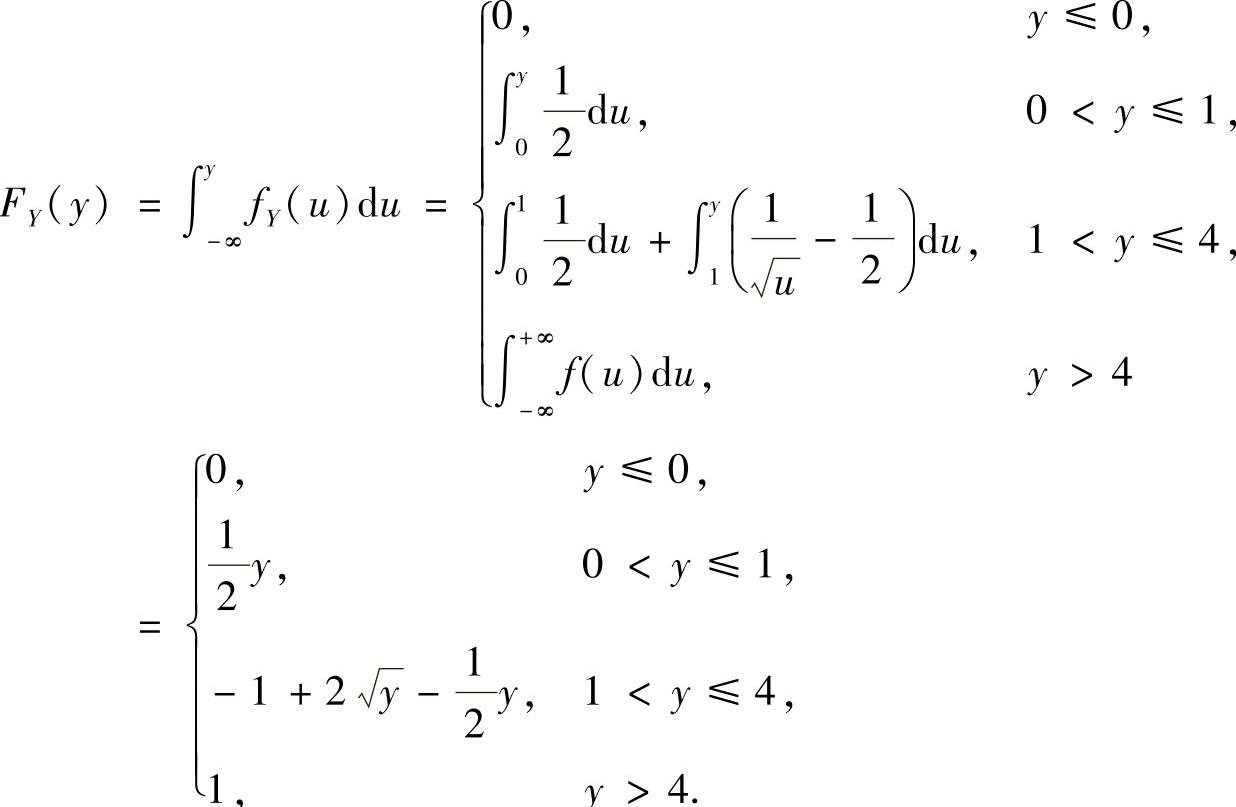

三、解答题

（15）

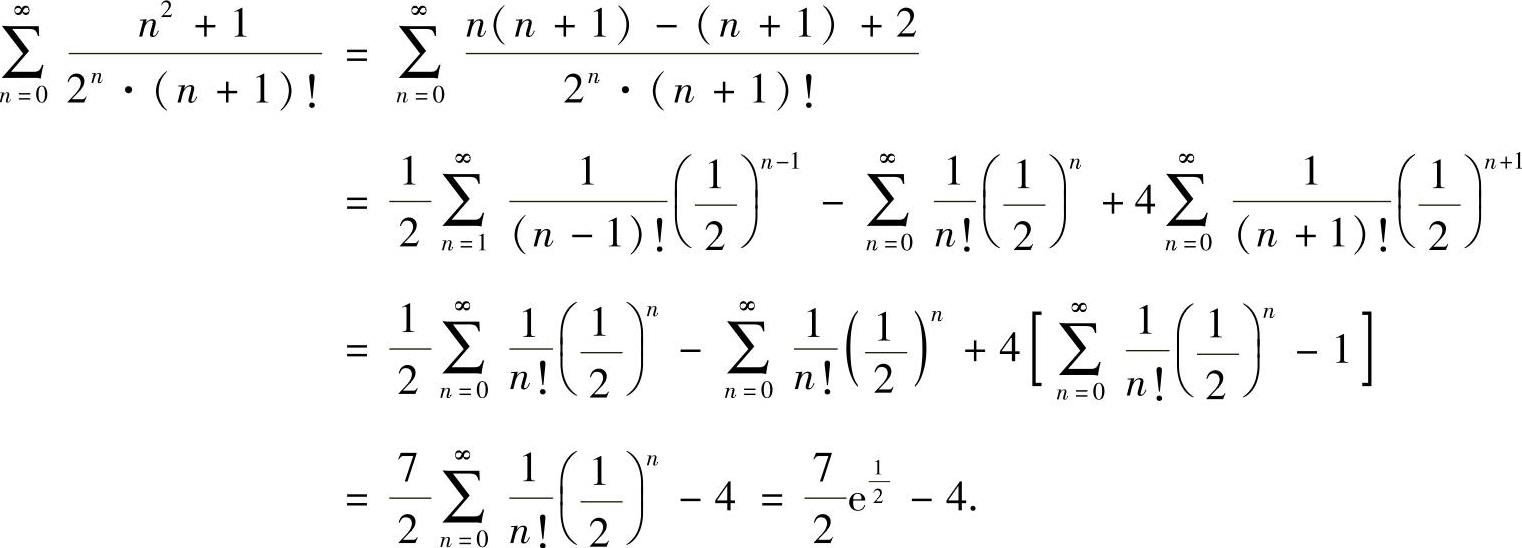
附注 利用常用函数e^x，sinx，cosx，ln（1+x），（1+x）μ的麦克劳林级数计算级数和是经常采用的方法.本题是利用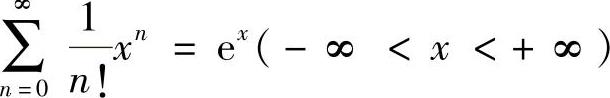计算所给级数之和.(www.xing528.com)

（16）

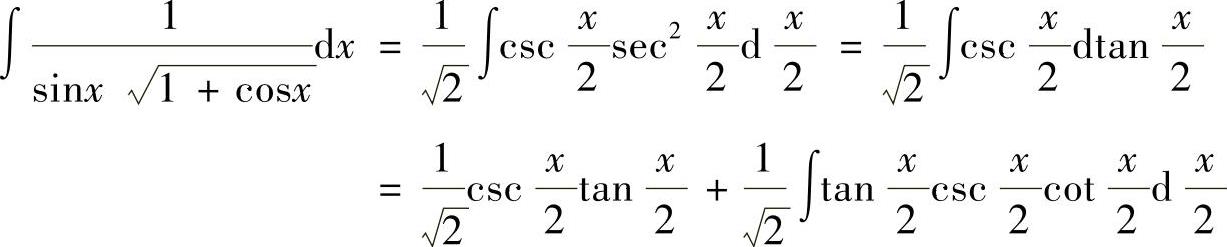
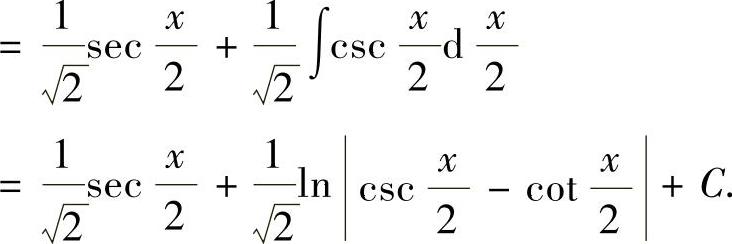
附注 应记住以下积分公式：

（17）对于x∈（-∞，+∞）有

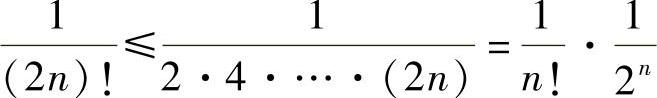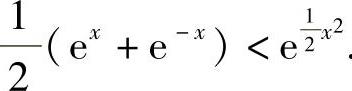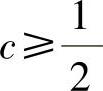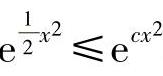于是由 （n=0，1，2，…，且仅当n=0，1时取等号）知，由此可知，当时，由得证

附注 本题还可用反证法证明仅当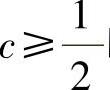时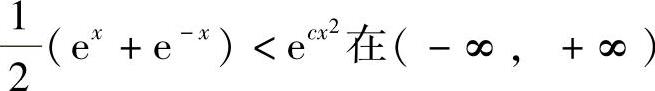，上才成立.具体如下：

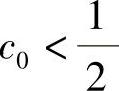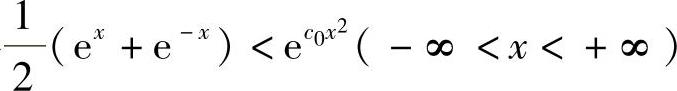设存在，使得，（1）

则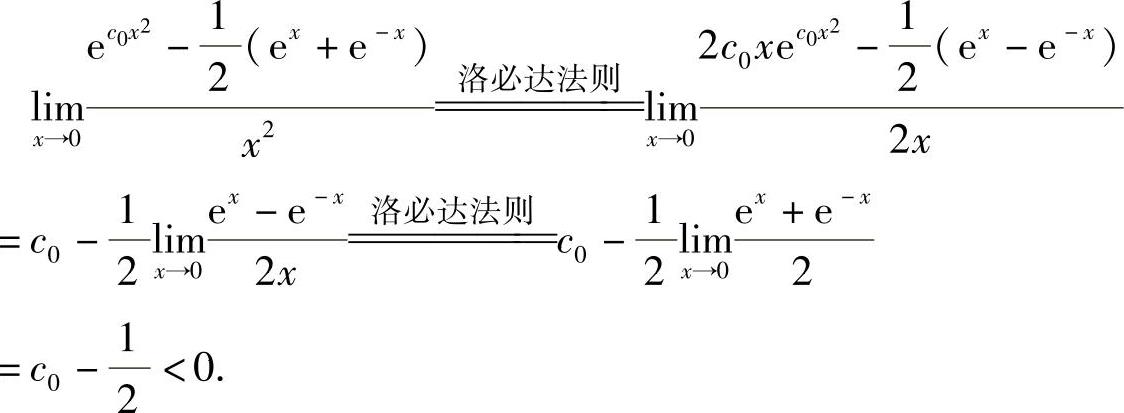

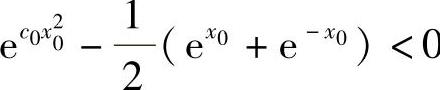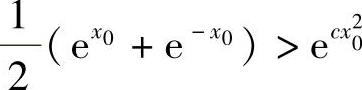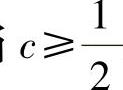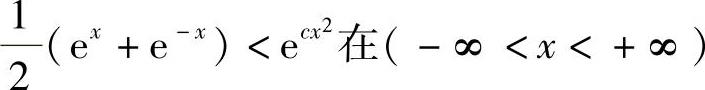故存在实数x₀，使得，即.这与式（1）矛盾.因此仅当时，上才成立.

（18）由于D（t）={（x，y）|x²+y²≤t²}，L（t）={（x，y）|x²+y²=t²}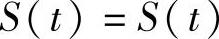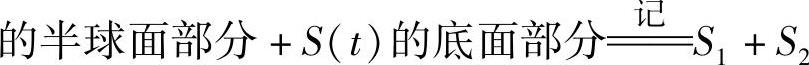，，所以

于是由题设得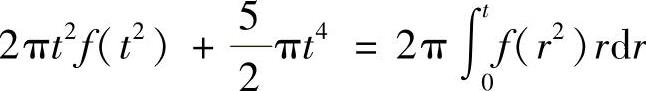，即

上式两边对t求导得

所以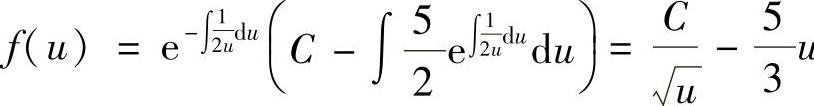，u，即

由于f（t）在[0，+∞）上连续，所以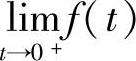存在，因此C=0.从而

附注 题解中值得注意的是常数C的确定，即利用f（t）在[0，+∞）上连续，推出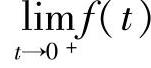存在，从而C=0.

（19）由于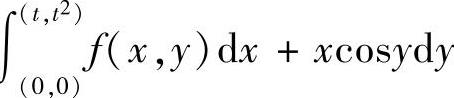 与积分路径无关，所以有

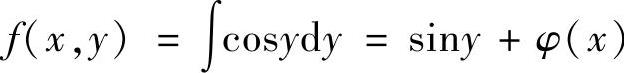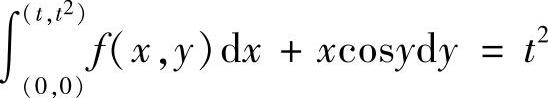于是，.将它代入得

即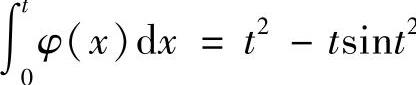.两边对t求导得

φ（t）=2t-sint²-2t²cost².

从而，f（x，y）=siny+2x-sinx²-2x²cosx².

附注 由表达式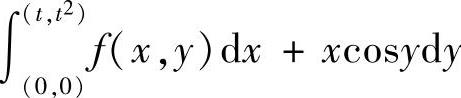可知，该曲线积分与积分路径无关，因此有式（1）.

（20）使矩阵方程AX=B有解，必须

r（A）=r（A┈B）.

由于

所以，使式（1）成立的a，b，c满足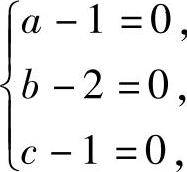

即a=1，b=2，c=1.

当a=1，b=2，c=1时，所给的矩阵方程与

同解.记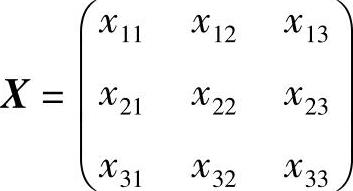，则式（1）等价于以下三个线性方程组

式（2）的通解为（x₁₁，x₂₁，x₃₁）^T=C₁（-1，-1，1）^T+（1，0，0）^T=（-C₁+1，-C₁，C₁）^T，

式（3）的通解为（x₁₂，x₂₂，x₃₂）^T=C₂（-1，-1，1）^T+（2，2，0）^T=（-C₂+2，-C₂+2，C₂）^T，

式（4）的通解为（x₁₃，x₂₃，x₃₃）^T=C₃（-1，-1，1）^T+（1，-1，0）^T=（-C₃+1，-C₃-1，C₃）^T.

所以，式（1），即所给矩阵方程的所有解为

附注 （Ⅰ）设矩阵方程AX=B（其中A，B分别为m×n，m×l矩阵），则

AX=B有解的充分必要条件为r（A┈B）=r（A）.特别，AX=B有唯一解的充分必要条件r（A┈B）=r（A）=n；AX=B有无穷多解的充分必要条件是r（A┈B）=r（A）＜n.

（Ⅱ）当矩阵方程AX=B有解时，可按以下方法求解：

如果A可逆（此时m=n），则X=A^-1B；

如果A不可逆，则如题解中那样，将AX=B表示成若干个线性方程组，然后逐一计算各个方程组的通解，即可得到X.

（21）由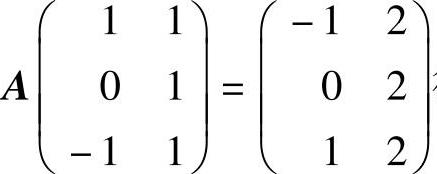得

所以，A有特征值-1，2，它们对应的特征向量分别为ξ₁=（1，0，-1）^T，ξ₂=（1，1，1）^T.由于r（A）=2，所以A还有特征值0，设它对应的特征向量为ξ₃=（a，b，c）^T，则由A是实对称矩阵知ξ₃满足

取它的基础解系为ξ₃，即ξ₃=（1，-2，1）^T.

显然，ξ₁，ξ₂，ξ₃是正交向量组，现将它们单位化：

记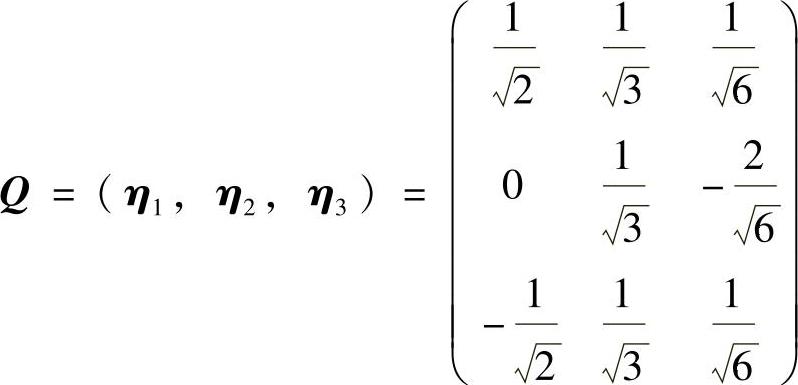（正交矩阵），则正交变换y=Cx将f（x₁，x₂，x₃）化为标准形-y²₁+2y²_2.

附注 应熟练掌握用正交变换或可逆线性变换（即配平方法）将二次型化为标准形的方法.

（22）记（X，Y）关于X与Y的边缘概率密度分别为f_X（x）与f_Y（y），则

（Ⅰ）由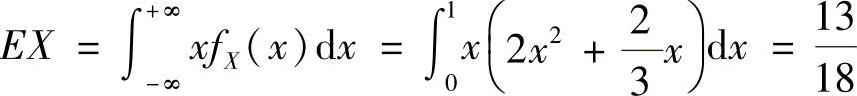得

其中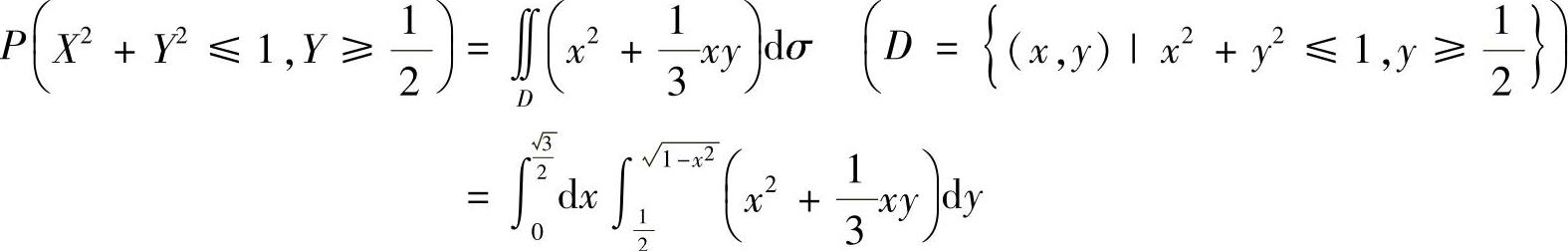

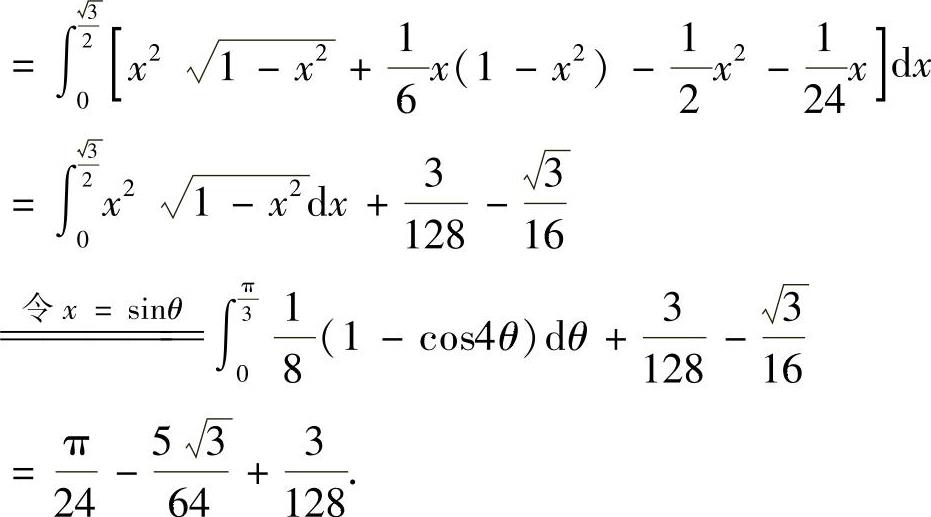
附注 题解中需注意的是

而不是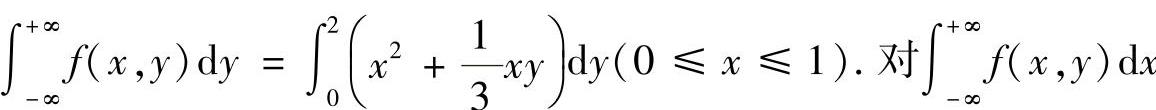也有同样的说法.

（23）设Z的简单随机样本Z₁，Z₂，…，Z_n的观察值为z₁，z₂，…，z_n，则似然函数为

取对数得

所以有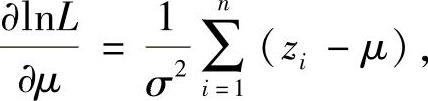

由最大似然估计法，令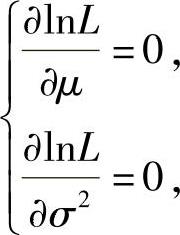得_μ，σ²的最大似然估计值分别为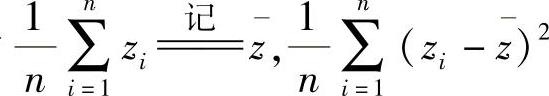，所以μ，σ²的最大似然估计量分别为

由于EX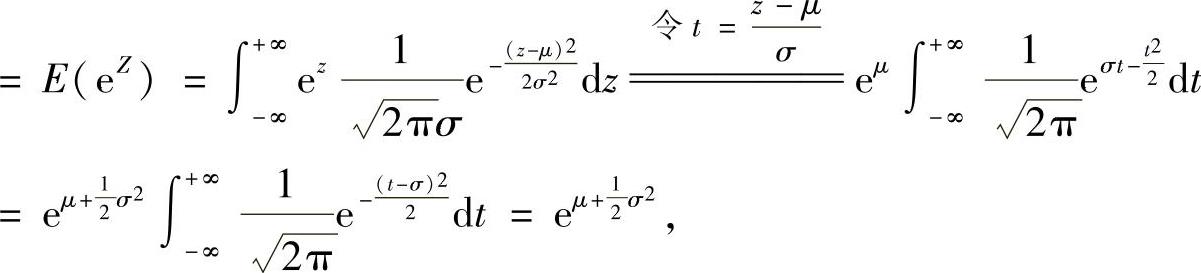

所以，由最大似然估计量的不变性得EX的最大似然估计量为

附注 （Ⅰ）应记住，设总体X～N（μ，σ²），X₁，X₂，…，X_n是来自X的简单随机样本，则

μ的矩估计量=μ的最大似然估计量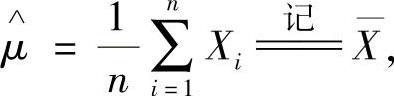

σ²的矩估计量=μ的最大似然估计量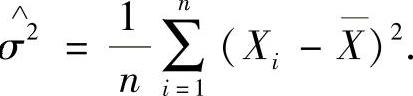

（Ⅱ）最大似然估计量的不变性是：

设θ是未知参数，θ的函数u=u（θ）有单值反函数，则当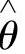是θ的最大似然估计量时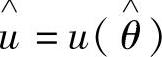，是u（θ）的最大似然估计量.