一、选择题
答案
(1)当|x|≤1时,由1≤ 知
知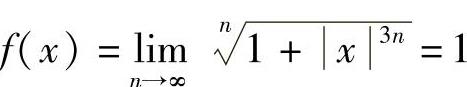 ;
;
当x>1时, ,所以
,所以
显然f(x)在(-∞,-1)∪(-1,1)∪(1,+∞)上可导,但由
知,f(x)在点x=1处不可导.此外,由f(x)是偶函数知f(x)在点x=-1处也不可导.因此选(C).
附注 由于f(x)是由数列极限确定的,所以要讨论它的可导性,首先要通过数列极限计算,确定f(x)的解析表达式.
(2)由于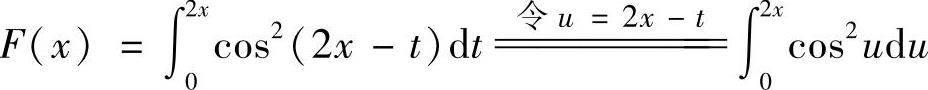 ,所以
,所以
F′(x)=2cos22x,F″(x)=-4sin4x.
因此选(D).
附注 要计算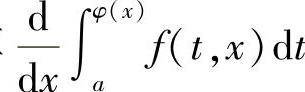 时,首先应将被积函数中的x移到积分号外,或移到积分限中去.
时,首先应将被积函数中的x移到积分号外,或移到积分限中去.
(3)由于当AC-B2=0时,f(x0,y0)可能是极值,也可能不是极值,所以选项(C)不正确.因此选(C).
附注 (C)的不正确性可用下列例子说明:
设f1(x,y)=x3+y3,记(x0,y0)=(0,0),则f′x(x0,y0)=f′y=(x0,y0)=0,且AC-B2=0.此时,f(x0,y0)=0不是f(x,y)的极值.
设f2(x,y)=x4+y4,记(x0,y0)=(0,0),则f′x(x0,y0)=f′y(x0,y0)=0,
且 AC-B2=0.此时,f(x0,y0)=0是f(x,y)的极值(极小值).
(4)由于Ω关于xOy平面对称,也关于yOz平面对称,且被积函数z在对称点处的值不变,所以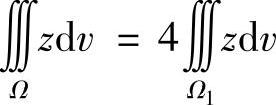 .因此选(C).
.因此选(C).
附注 设三重积分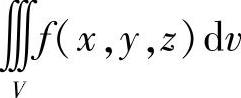 .如果V具有某种对称性,且f(x,y,z)在对称点处的值彼此相等(或互为相反数),则
.如果V具有某种对称性,且f(x,y,z)在对称点处的值彼此相等(或互为相反数),则
其中V1是V按上述的对称性划分成的两部分之一.
(5)由于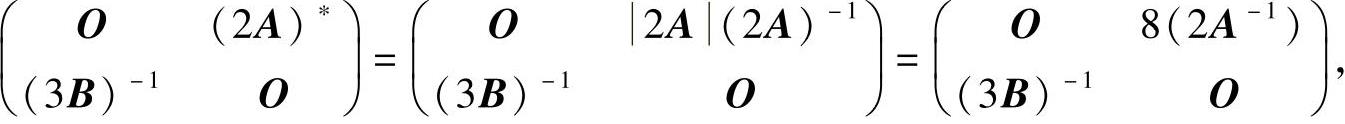 所以,
所以, .因此选(B).
.因此选(B).
附注 题解中应用了以下公式(应记住):
设A是n阶矩阵,则|A∗|=|A|n-1(n≥2),|kA|=kn|A|(k是常数).
设A是n阶可逆矩阵,则A∗=|A|A-1.
设A,B分别是m,n阶可逆矩阵,则
(6)由题设知r(P)+r(Q)≤3.由于当t≠6时,r(Q)=2,所以此时r(P)≤1.此外,由P是非零矩阵知,r(P)≥1.从而r(P)=1.因此选(C).
附注 本题也可按以下方法计算:
当t≠6时,r(QT)=2,所以齐次线性方程组QTx=0的基础解系中只包含3-2=1个线性无关的解向量.从而由QTPT=O知,非零矩阵PT的线性无关列向量个数为1,即得r(P)=r(PT)=1.
(7)记A1={第一次取到的是一等品},
A2={第二次取到的是一等品},则 ,其中
,其中
所以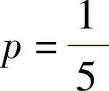 .因此选(A).
.因此选(A).
附注 题解中的P(A1∪A2)也可按加法公式计算:
显然,它没有题解中的计算简捷.
(8)由于 ,所以由列维—林德柏格中心极限定理得
,所以由列维—林德柏格中心极限定理得
因此选(A).
附注 列维—林德伯格中心极限定理是:
设X1,X2,…,Xn,…是相互独立同分布的随机变量序列,它们的数学期望都为μ,方差都为σ2,则对任意实数x,有
其中,Φ(x)是标准正态分布函数.
二、填空题
(9)由于f(0)=0;x<0时,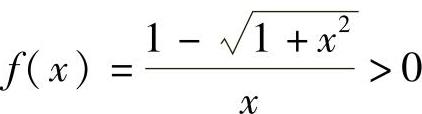 ;x>0时,
;x>0时, ,所以方程f(x)=0的实根个数为1.
,所以方程f(x)=0的实根个数为1.
附注 题解中应注意的是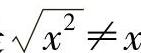 ,而
,而 .
.
(10)记 ,则
,则
所以,
于是 f(x)=x+2-π,从而
附注 本题获解的关键,是注意到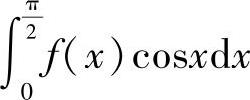 是常数.
是常数.
(11)由 ,所以
,所以
附注 计算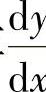 时,要注意y是x的函数,而
时,要注意y是x的函数,而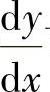 可由方程ex+siny=x两边对x求导得到.
可由方程ex+siny=x两边对x求导得到.
(12)由于所给微分方程可以改写成
(xcosydy+sinydx)+(cosxdy-ysinxdx)=0,
即 d(xsiny+ycosx)=0. 因此通解为xsiny+ycosx=C.
附注 对于微分方程P(x,y)dx+Q(x,y)dy=0,有时将P(x,y)dx+Q(x,y)dy,经适当转换后分成若干组,使各组分别是某个二元函数的全微分,由此得到所给微分方程的通解.本题就是按此方法求解的,十分快捷.
(13)由于A~B,所以B有特征值-2,-1,1,2,从而B∗有特征值
所以
附注 题解有两点值得注意:
(Ⅱ)设A,B是相似的n阶矩阵,则A-En=B-En.
(14)由于E(X3+2Y2)=E(X3)+2E(Y2),其中
所以,
附注 在E(X3)的计算中,对于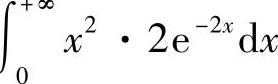 不必再作积分计算,这是因为它可由
不必再作积分计算,这是因为它可由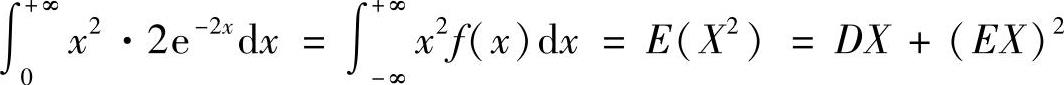 直接得到.
直接得到.
三、解答题
(15)由于y″+y=0的特征方程的根为λ=-i,i,所以它的通解为Y=C1cosx+C2sinx.此外,所给微分方程
y″+y=5e2x+2sinx(1)
应有特解y∗=Ae2x+x(B1cosx+B2sinx).将它代入式(1)得
5Ae2x-2B1sinx+2B2cosx=5e2x+2sinx.
由此得到A=1,B1=-1,B2=0.所以,y∗=e2x-xcosx,从而式(1)的通解为y=Y+y∗=C1cosx+C2sinx+e2x-xcosx.
附注 应记住常系数线性微分方程的解法.
(16)(Ⅰ)显然{an}是正项数列,且由
界.此外,由
知,{an}单调不增.从而由数列极限存在准则知,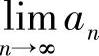 存在,记为a.对递推式两边取极限得
存在,记为a.对递推式两边取极限得 ,所以a=1,即
,所以a=1,即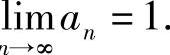
(Ⅱ)由于 ,所以所给幂级数的收敛半径R=2.
,所以所给幂级数的收敛半径R=2.
当x=2,-2时,所给幂级数分别为 ,显然它们的通项极限都不为零,所以所给幂级数在点x=2,-2处都是发散的,故收敛域为(-1,1).
,显然它们的通项极限都不为零,所以所给幂级数在点x=2,-2处都是发散的,故收敛域为(-1,1).
附注 计算幂级数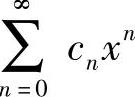 的收敛域步骤如下:(https://www.xing528.com)
的收敛域步骤如下:(https://www.xing528.com)
(Ⅰ)计算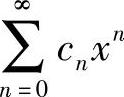 的收敛半径,记为R.
的收敛半径,记为R.
(Ⅱ)当R=+∞时, 的收敛域为(-∞,+∞);当R=0时,
的收敛域为(-∞,+∞);当R=0时,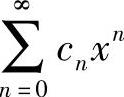 的收敛域为{0};当R为正数时,
的收敛域为{0};当R为正数时, 的收敛域为(-R,R)与其收敛端点之并集.
的收敛域为(-R,R)与其收敛端点之并集.
(17)记A ,则
,则 于是有
于是有
即
所以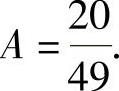 从而
从而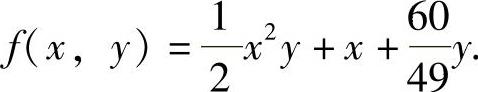
由于在D内,f′x=xy+1>0,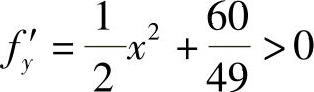 ,所以f的最值只能在D的边界C1:y=0(0≤x≤1),C2:x=1(0≤y≤1)及C3:y=x2(0≤x≤1)上取到.
,所以f的最值只能在D的边界C1:y=0(0≤x≤1),C2:x=1(0≤y≤1)及C3:y=x2(0≤x≤1)上取到.
在C1上,f(x,y)=x(0≤x≤1),故最大值为1,最小值为0.
在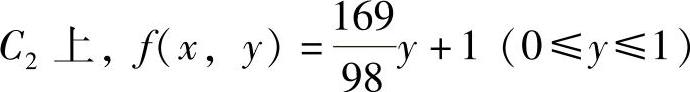 ,故最大值为
,故最大值为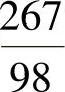 ,最小值为1.
,最小值为1.
在C3上,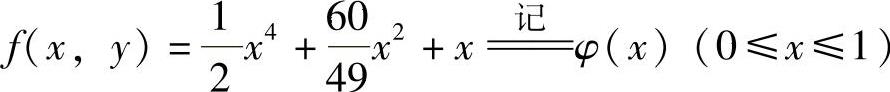 .由于在(0,1)上,
.由于在(0,1)上,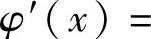
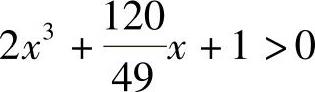 ,所以f(x,y)在C3上的最大值为
,所以f(x,y)在C3上的最大值为 ,最小值为φ(0)=0.
,最小值为φ(0)=0.
因此,f(x,y)在D上的最大值为 ,最小值为0.
,最小值为0.
附注 二元连续函数f(x,y)在有界闭区域D上的最值计算步骤如下:
第一步 计算f(x,y)在D的内部的可能极值点,记为
(x1,y1),(x2,y2),…,(xn,yn).
第二步 计算f(x,y)在D的边界C上的最大值与最小值,分别记为M1与m1,则f(x,y)在D上的最大值为
M=max{f(x1,y1),f(x2,y2),…,f(xn,yn),M1};
最小值为
m=min{f(x1,y1),f(x2,y2),…,f(xn,yn),m1}.
(18)作辅助函数F(x)=f(x)-x,则F(x)在[0,1]上连续,且
F(0)F(1)=f(0)[f(1)-1]<0,
所以由零点定理知,存在ξ∈(0,1),使得F(ξ)=0,即f(ξ)=ξ.(1)
下面用反证法证明ξ的唯一性.设另有η∈(0,1),使得f(η)=η,不妨设η<ξ,则
f(ξ)-f(η)=ξ-η.
由拉格朗日中值定理知,存在θ∈(η,ξ)⊂(0,1),使得
f′(θ)(ξ-η)=ξ-η,即f′(θ)=1.
这与题设f′(x)≠1(x∈[0,1])矛盾.因此满足式(1)的ξ是唯一的.
附注 唯一性问题,往往用反证法证明.本题就是如此.
(19)由于 z′x(0,0)=f′x(0,0)+f′y(0,0)·f′x(0,0)=0,
z′y(0,0)=f′y(0,0)·f′y(0,0)=1,
所以,π的方程为z′x(0,0)(x-0)+z′y(0,0)(y-0)-(z-0)=0,即z=y.
于是,C的方程为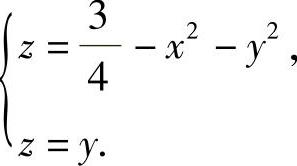
由此得到
附注 在计算关于坐标的曲线积分 时,用C的方程消去Pdx+Qdy+Rdz中的一个积分变量,例如消去z,则所给的曲线积分化简为
时,用C的方程消去Pdx+Qdy+Rdz中的一个积分变量,例如消去z,则所给的曲线积分化简为 (其中Cxy是C在xOy平面的投影),于是通过它的计算即得
(其中Cxy是C在xOy平面的投影),于是通过它的计算即得

这是比较快捷的方法,本题的曲线积分就是按此法计算的.
(20)由于

所以由题设知, 即a=2,b=8,c=-10.此时所给方程组与(Ⅱ)
即a=2,b=8,c=-10.此时所给方程组与(Ⅱ)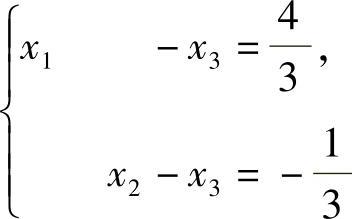 同解.(Ⅱ)的导出组的基础解系为C(1,1,1)T,此外(Ⅱ)有特解
同解.(Ⅱ)的导出组的基础解系为C(1,1,1)T,此外(Ⅱ)有特解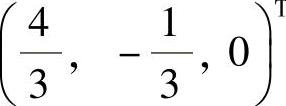 ,所以(Ⅰ)的通解为
,所以(Ⅰ)的通解为
对上述算得的a,b,c知,
设ξ在基η1,η2,η3下的坐标为y1,y2,y3,则
比较式(1)与式(2)得
即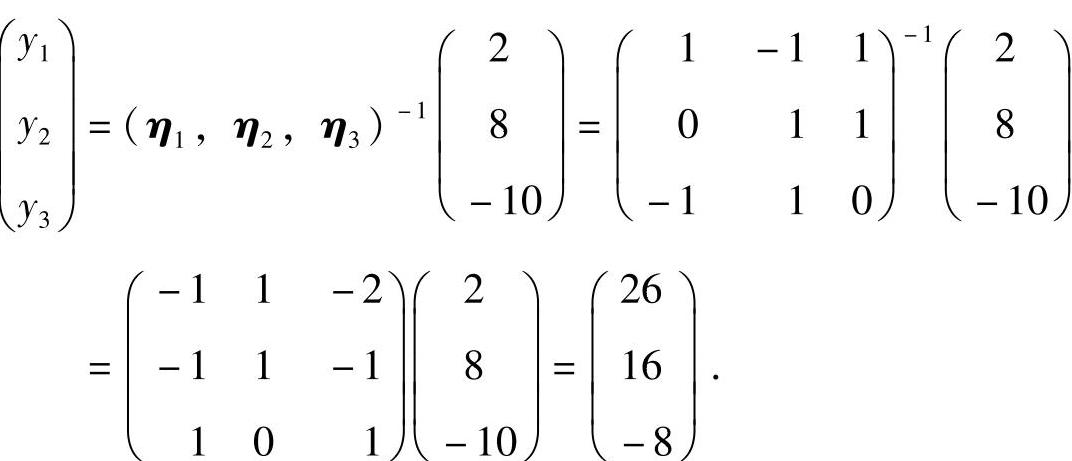
所以,所求的坐标为26,16,-8.
附注 由所给方程组有两个不同解可得,这个方程组对应的齐次线性方程有非零解,所以系数矩阵的秩≤2,此外由系数矩阵本身可知,其秩≥2.因此系数矩阵的秩=2.从而有
(21)由于 即可逆线性变换
即可逆线性变换 下成为y21+y22+y23,所以g(x1,x2,x3)是正定二次型,其规范形为y21+y22+y23.
下成为y21+y22+y23,所以g(x1,x2,x3)是正定二次型,其规范形为y21+y22+y23.
由于f(x1,x2,x2)是非正定二次型,所以,它的矩阵
的顺序主子式不全为正,故有c≤2.从而由题设c≥2得c=2.于是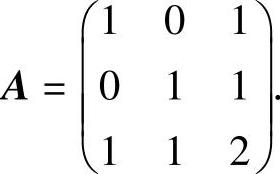
由于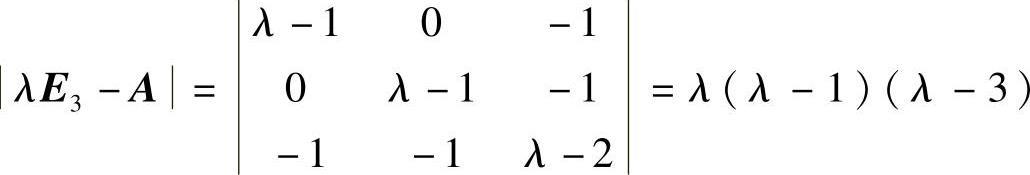 ,所以A有特征值λ=0,1,3.
,所以A有特征值λ=0,1,3.
设A的对应λ=0的特征向量为ξ=(a1,a2,a3)T,则它满足
可取它的基础解系为ξ,即ξ=(-1,-1,1)T.
设A的对应λ=1的特征向量为η=(b1,b2,b3)T,则它满足
可取它的基础解系为η,即η=(1,-1,0)T.
设A的对应λ=3的特征向量为ζ=(c1,c2,c3)T,则由A是实对称矩阵知
可取它的基础解系为ζ,即ζ=(1,1,2)T.
显然,ξ,η,ζ是正交向量组,现将它们单位化:
记 (正交矩阵),则正交变换x=Qz(其中x=(x1,x2,x3)T,z=(z1,z2,z3)T)将f(x1,x2,x3)化为标准形z22+3z33.
(正交矩阵),则正交变换x=Qz(其中x=(x1,x2,x3)T,z=(z1,z2,z3)T)将f(x1,x2,x3)化为标准形z22+3z33.
附注 由于φ(x1,x2,x3)=(x1,x2,x3)B(x1,x2,x3)T(B是实对称矩阵)为正定二次型的充分必要条件是它的矩阵B的顺序主子式都大于零.故当题中f(x1,x2,x3)不是正定二次型时,它的矩阵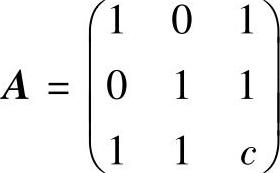 的顺序主子式1,
的顺序主子式1,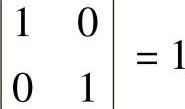 ,A=c-2不全大于零,于是有c≤2.
,A=c-2不全大于零,于是有c≤2.
(22)由于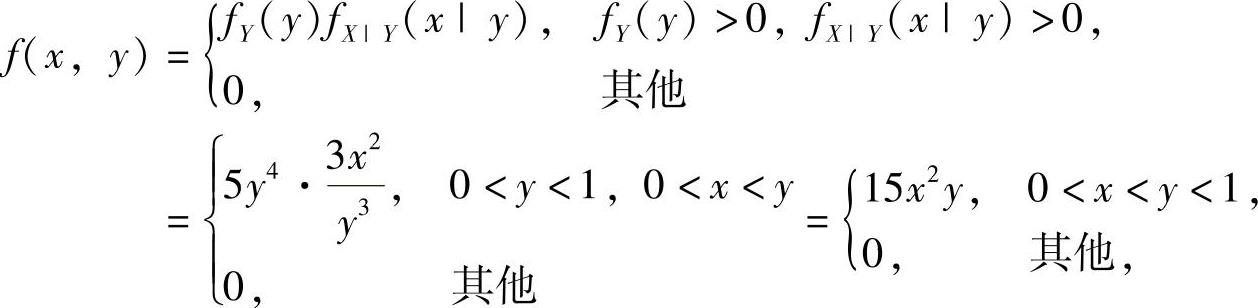
所以,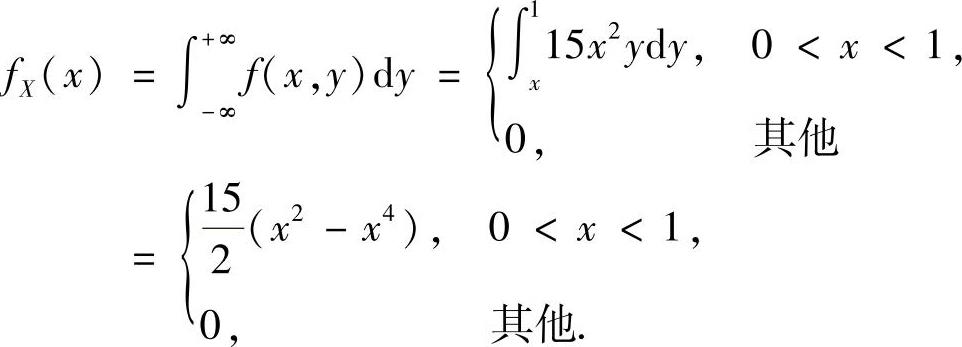
于是由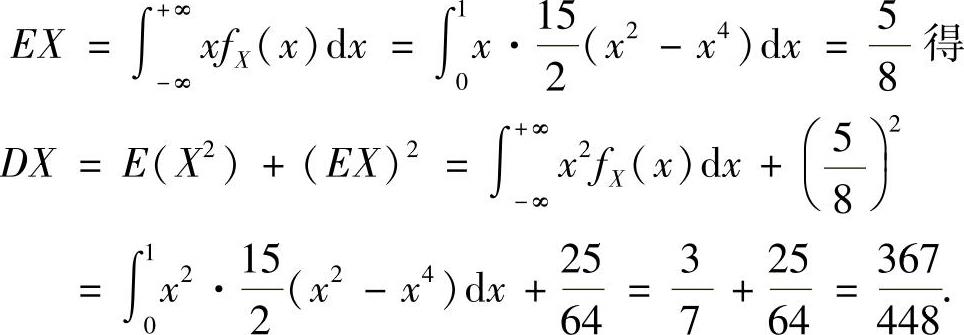
此外,由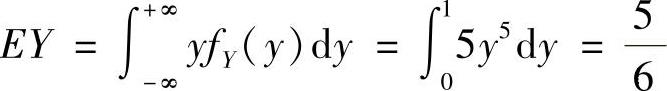 得
得
附注 当已知fY(y),fX|Y(x|y)时,可按以下公式计算f(x,y):
同样当已知fX(x),fY|X(y|x)时,可按以下公式计算f(x,y):
(23)记Z的分布函数为F(z),则
所以,Z的概率密度为
由此得到似然函数
即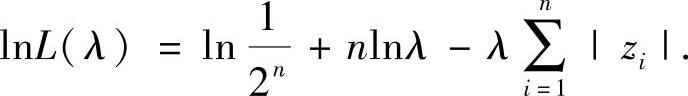
上式两边对λ求导得
于是由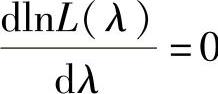 得λ的最大似然估计值为
得λ的最大似然估计值为
附注 应熟练掌握参数点估计的两种方法:矩估计法与最大似然估计法.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




