一、选择题:1~8小题,每小题4分,共32分.每小题给出的四个选项中,只有一个选项是符合题目要求的,请将选项前的字母填在答∙题∙纸∙指定位置上.
(1)方程2x-x2-1=0的不同实根个数为
(A)1. (B)2. (C)3. (D)4.
[ ]
(2)设F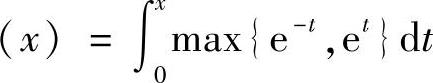 ,则
,则
[ ]
(3)设{an}是单调减少收敛于零的正项数列,则当级数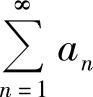 发散时,下列结论正确的是
发散时,下列结论正确的是
(A)级数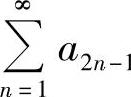 收敛,而级数
收敛,而级数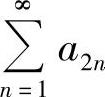 发散.
发散.
(B)级数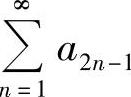 发散,而级数
发散,而级数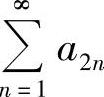 收敛.
收敛.
(C)级数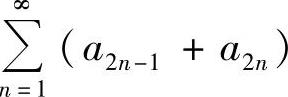 收敛.
收敛.
(D)级数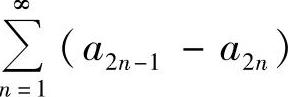 收敛.
收敛.
[ ]
(4)设Σ是半球面x2+y2+z2=4(z≥0)的上侧,则曲面积分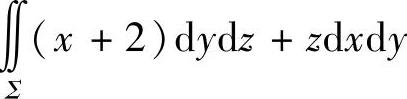 等于
等于
其中Dxy,Dyz分别是Σ在xOy平面与yOz平面的投影.
[ ]
(5)设向量组α,β,γ线性无关,向量组α,β,δ线性相关,则
(A)δ可由α,β,γ线性表示,且表示式是唯一的.
(B)δ可由α,β,γ线性表示,但表示式不是唯一的.
(C)β不可由α,γ,δ线性表示.
(D)δ不可由α,β,γ线性表示.
[ ]
(6)设A是n阶矩阵以及以下命题:
① A有n个不同的特征值.
② A有n个线性无关的特征向量.
③ A是实对称矩阵.
④ A的每个ni重特征值λi的特征矩阵λiEn-A都满足r(λiEn-An)=n-ni.则A可相似对角化的充分必要条件是
(A)①②. (B)②③. (C)②④. (D)①④.
[ ]
(7)下列命题中不∙正∙确∙的是
(A)设二维随机变量(X,Y)在矩形区域{(x,y)a≤x≤b,c≤y≤d}上服从均匀分布,则X与Y相互独立.
(B)设二维随机变量(X,Y)的概率密度
则X与Y相互独立.
(C)设二维随机变量(X,Y)在圆域{(x,y)x2+y2≤R2}上服从均匀分布(其中,R是正数),则X,Y相互独立.
(D)设X1,X2,X3,X4是来自同一总体的简单随机样本,则随机变量X=f1(X1,X2),Y=f2(X3,X4)(其中,f1,f2都是连续函数)相互独立.
[ ]
(8)设总体X~N(μ1,σ2),Y~N(μ2,σ2),它们相互独立,又设X1,X2,…,Xn1和Y1,Y2,…,Yn2是分别来自X和Y的简单随机样本,记
则DZ为
[ ](https://www.xing528.com)
二、填空题:9~14小题,每小题4分,共24分.请将答案写在答∙题∙纸∙指定位置上.
(9)设极限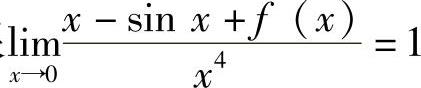 ,则极限
,则极限
(10)设函数z=f(x+y,yg(x)),其中,f具有2阶连续偏导数,曲线w=g(x)在点(0,1)处的切线方程为w=1+x,且f(u,v)的各阶偏数在u=v处的值都为1,则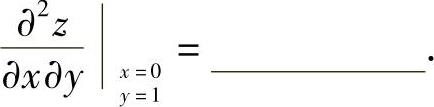
(11)曲面z=x2+y2被上半球面x2+y2+z2=2(z≥0)截下的有限部分Σ的面积为____.
(12)设函数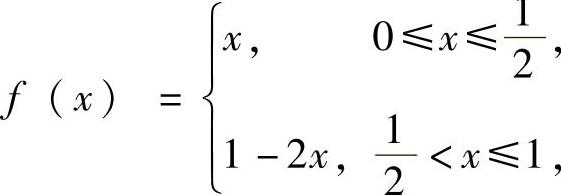 其余弦级数与正弦级数的和函数分别为s1(x)与s2(x),则s1(-1)与
其余弦级数与正弦级数的和函数分别为s1(x)与s2(x),则s1(-1)与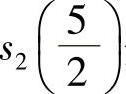 分别为____.
分别为____.
(13)设A,B分别为2阶与4阶矩阵,且r(A)=1,r(B)=2,A∗,B∗分别是A与B的伴随矩阵,则
(14)设随机变量X与Y相互独立,都服从参数为1的指数分布,即它们的概率密度都为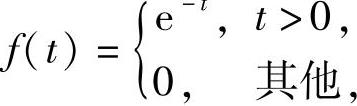 则p(max{X,Y}≤1)=____.
则p(max{X,Y}≤1)=____.
三、解答题:15~23小题,共94分.请将解答写在答∙题∙纸∙指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
设函数y(x)在[0,+∞)上有连续导数,且满足
求y(n)(x).
(16)(本题满分10分)
求三元函数f(x,y,z)=2x+2y+x2+y2-z2在Ω:x2+y2+z2≤1上的最大值与最小值.
(17)(本题满分10分)
证明:当 时,2sinx+tanx>3x.
时,2sinx+tanx>3x.
(18)(本题满分10分)
设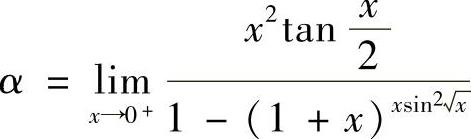 ,求级数
,求级数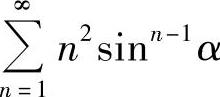 的和.
的和.
(19)(本题满分10分)
计算曲线积分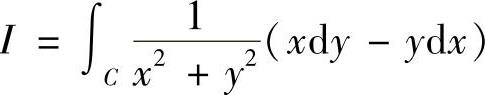 ,其中,C为曲线
,其中,C为曲线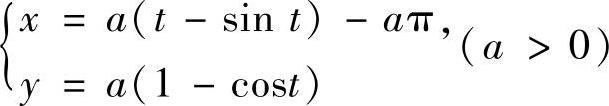 从t=0到t=2π的一段.
从t=0到t=2π的一段.
(20)(本题满分11分)
已知线性方程组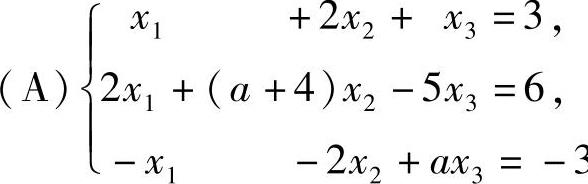 有无穷多解.
有无穷多解.
(Ⅰ)求常数a的值.
(Ⅱ)对上述算得的a值,求方程组(A)与及公共解.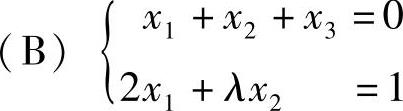 ,有公共解时的λ值
,有公共解时的λ值
(21)(本题满分11分)
设A是3阶实对称矩阵,其秩为2,且满足
(Ⅰ)求A∗;
(Ⅱ)求正交变换x=Cy(其中,x=(x1,x2,x3)T,y=(y1,y2,y3)T,C为正交矩阵),使得二次型f(x1,x2,x3)=xT(A∗+A)x成为标准形,并写出该标准形.
(22)(本题满分11分)
设二维随机变量(U,V)的概率密度为
又设X与Y都是离散型随机变量,其中X只取-1,0,1三个值,Y只取-1,1两个值,且EX=0.2,EY=0.4,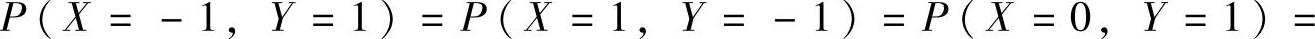
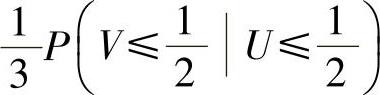 .求
.求
(Ⅰ)(X,Y)的概率分布.
(Ⅱ)Cov(X,Y).
(23)(本题满分11分)
设二维随机变量(X,Y)的概率密度为
其中,θ是未知参数,又设X1,X2,…,Xn是来自总体X的简单随机样本.
(Ⅰ)计算θ的矩估计量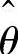 ,并判断
,并判断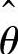 是否为无偏估计量.
是否为无偏估计量.
(Ⅱ)求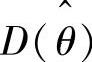 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




