一、选择题:1~8小题,每小题4分,共32分.每小题给出的四个选项中,只有一个选项是符合题目要求的,请将所选项前的字母填在答∙题∙纸∙指定位置上.
(1)设函数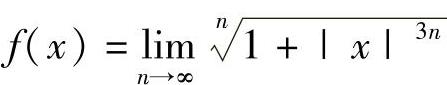 ,则f(x)在(-∞,+∞)上
,则f(x)在(-∞,+∞)上
(A)处处可导. (B)恰好有一个不可导点.
(C)恰好有两个不可导点.(D)至少有三个不可导点.
[ ]
(2)设函数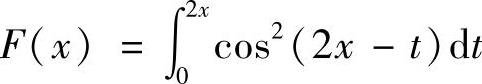 ,则F″(x)为
,则F″(x)为
(A)4sin4x. (B)4cos4x. (C)-4cos4x. (D)-4sin4x.
[ ]
(3)设二元函数f(x,y)在点(x0,y0)的某个邻域内具有二阶连续偏导数,且f′x(x0,y0)=f′y(x0,y0)=0,记A=f″xx(x0,y0),B=f″xy(x0,y0),C=f″yy(x0,y0),则以下结论不∙正∙确∙的是
(A)当A>0,AC-B2>0时,f(x0,y0)是极小值.
(B)当C>0,AC-B2>0时,f(x0,y0)是极小值.
(C)当AC-B2=0时,f(x0,y0)不是极值.
(D)当AC-B2<0时,f(x0,y0)不是极值.
[ ]
(4)设空间区域Ω={(x,y,z)|x2+y2+z2≤R2,z≥0}(其中R>0)和Ω1={(x,y,z)|x2+y2+z2≤R2,x≥0,y≥0,z≥0},则下列四式中正确的是
[ ]
(5)设A是2阶矩阵,且A=2,B是3阶可逆矩阵,则分块矩阵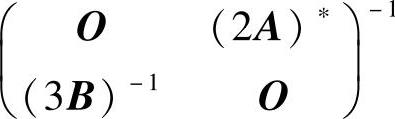 等于
等于
[ ]
(6)已知矩阵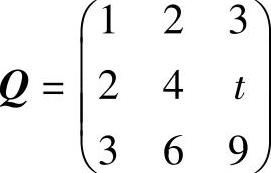
 及3阶非零矩阵P满足PQ=O,则
及3阶非零矩阵P满足PQ=O,则
(A)t=6时,r(P)=1. (B)t=6时,r(P)=2.
(C)t≠6时,r(P)=1. (D)t≠6时,r(P)=2.
[ ]
(7)在10件产品有4件一等品,6件二等品.现从中任取两次,每次取一件,取后不放回,已知其中至少有一件是一等品,则两件都是一等品的概率p为
[ ]
(8)设随机变量序列X1,X2,…,Xn,…相互独立且同服从参数为λ(λ>0)的指数分布,即它的概率密度同为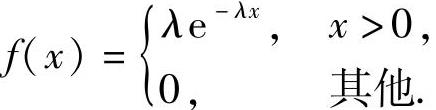 记Φ(x)为标准正态分布函数,则对任意实数x,下列结论中正确的为
记Φ(x)为标准正态分布函数,则对任意实数x,下列结论中正确的为
[ ]
二、填空题:9~14小题,每小题4分,共24分,请将答案写在答∙题∙纸∙指定位置上.
(9)设函数f(x)满足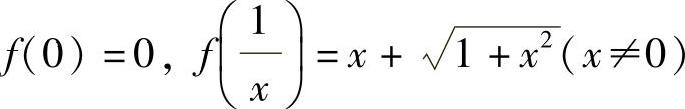 ,则方程f(x)=0的实根个数为____.
,则方程f(x)=0的实根个数为____.
(10)设函数f(x)连续,且满足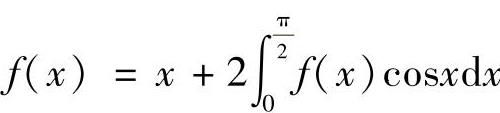 ,则定积分
,则定积分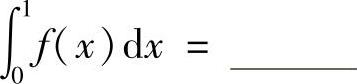
 (https://www.xing528.com)
(https://www.xing528.com)
(11)设z=f(ex,x2+y2),其中二元函数f(u,v)可微,且y=y(x)是由方程ex+siny=x确定的隐函数,则
(12)微分方程(xcosy+cosx)y′-ysinx+siny=0的通解为____.
(13)设A,B都是4阶矩阵,它们相似,且A的特征值为-2,-1,1,2,则行列式B∗-E4=____.
(14)设随机变量X的概率密度为 ,
,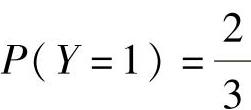 ,则E(X3+2Y2)=____.
,则E(X3+2Y2)=____.
三、解答题:15~23小题,共94分.请将解答写在答∙题∙纸∙指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
求微分方程y″+y=5e2x+2sinx的通解.
(16)(本题满分10分)
设数列{an}由递推式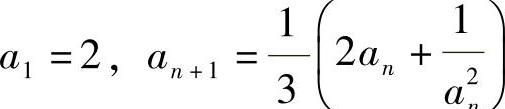 (n=1,2,…)确定,求
(n=1,2,…)确定,求
(Ⅰ)极限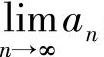 ;
;
(Ⅱ)幂级数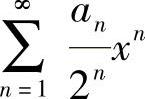 的收敛域.
的收敛域.
(17)(本题满分10分)
设二元函数f(x,y)满足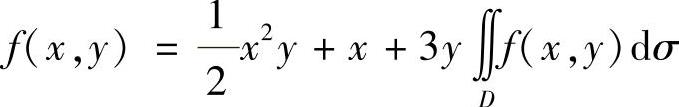 ,其中D是由曲线y=x2与
,其中D是由曲线y=x2与
直线x=1及x轴围成的平面图形,求f(x,y)在D上的最大值与最小值.
(18)(本题满分10分)
设函数f(x)在[0,1]上可导,且0<f(x)<1及f′(x)≠1,证明:存在唯一的ξ∈(0,1),使得f(ξ)=ξ.
(19)(本题满分10分)
设二元函数f(x,y)在点(0,0)的某个邻域内有定义,且f(0,0)=0,f′x(0,0)=3,f′y(0,0)=-1.记曲面z=f(x,f(x,y))在点(0,0)处的切平面为π,求曲线积分
其中C是π与曲面S: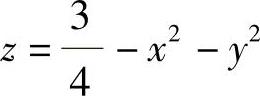 的交线,且从z轴正向看去,C是逆时针的.
的交线,且从z轴正向看去,C是逆时针的.
(20)(本题满分11分)
已知线性方程组(Ⅰ)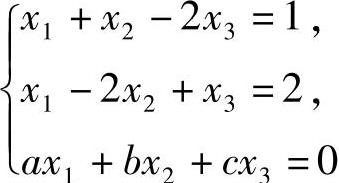 有两个不同的解,且a为系数矩阵的秩.求(Ⅰ)的通解及向量ξ=(a,b,c)T在基η1=(1,0,-1)T,η2=(-1,1,1)T,η3=(1,1,0)T下的坐标.
有两个不同的解,且a为系数矩阵的秩.求(Ⅰ)的通解及向量ξ=(a,b,c)T在基η1=(1,0,-1)T,η2=(-1,1,1)T,η3=(1,1,0)T下的坐标.
(21)(本题满分11分)
已知f(x1,x2,x3)=x21+x22+cx23+2x1x3+2x2x3(c≥2)与g(x1,x2,x3)=x21-2x1x2+4x22+x23中有且仅有一个是正定二次型,求常数c,并用可逆线性变换将正定二次型化为规范形以及用正交变换将非正定二次型化为标准形.
(22)(本题满分11分)
设有随机变量X与Y,其中Y的概率密度为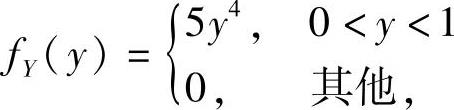 ,且在Y=y的条件下,X的条件概率密度为
,且在Y=y的条件下,X的条件概率密度为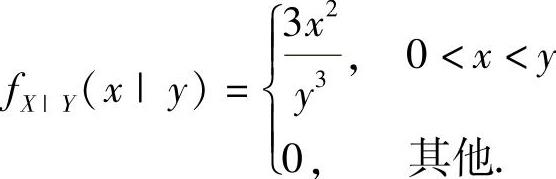 ,求DX及Cov(X,Y).
,求DX及Cov(X,Y).
(23)(本题满分11分)
设总体Z=XY,其中随机变量X与Y相互独立,且X的概率密度为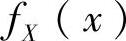
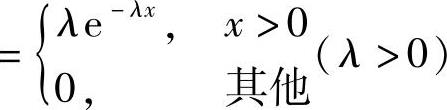 ,Y的概率分布为
,Y的概率分布为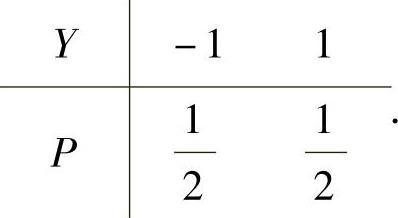 又设z1,z2,…,zn是来自Z的一个简单随机样本的观测值.求Z的未知参数λ的最大似然估计值.
又设z1,z2,…,zn是来自Z的一个简单随机样本的观测值.求Z的未知参数λ的最大似然估计值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




