Kuz-Ram模型及修正方法介绍

1.Kuz Ram模型

这一模型依据Kuznetsov方程和R—R 分布函数而提出。它从爆破参数导出R—R 分布函数的指数，将爆破参数与块度分布联系起来。

模型的基本表达式由Kuznetsov方程和R—R分布函数和块度不均匀指数三部分所组成：

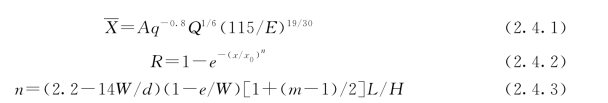
对于式（2.4.2），当R＝0.5 时，有：

此时，

上述式中：A为岩石系数，取值大小与岩石的节理、裂隙发育程度有关，中硬岩A＝7，节理发育坚硬岩A＝10，节理不发育坚硬岩A＝13；q 为炸药单耗，kg／m3；Q为单孔装药量，kg；E 为炸药相对重量威力，铵油炸药为100，TNT时为115；X 即X50，爆破岩块的平均粒径，cm；R 代表小于某粒径的石料质量百分数；X 为岩块颗粒直径，cm；X0为特征块度，即筛下累积率为63.21%时的块度尺寸，cm；n 为不均匀指数，表示分布曲线的陡缓；e 表示钻孔精度标准差，m；L 为不计超钻部分的装药长度，m；d 为炮孔直径，mm；W 为最小抵抗线，m；m为炮孔密集系数；H 为台阶高度，m。

由于Kuznetsov方程把爆破参数与爆破块度很好地联系起来，而R—R 分布函数被公认为是对爆破岩石破碎块度最合适的描述。因而Kuz Ram模型受到广泛采用，是有实用基础的。

2.Kuz Ram模型的修正

（1）关于A 的修正。岩体节理、裂隙对爆破的块度分布有很大影响。C.V.B.Cunningham根据现场反馈的实际资料，提出了岩石系数A确定的新方法。

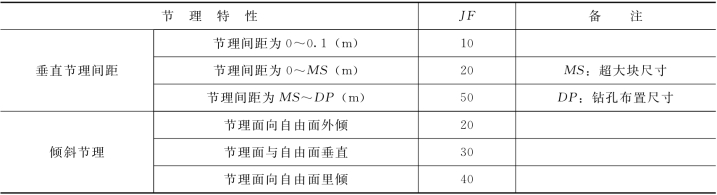
式中：RMD 为岩石性能系数，按表2.4.3 取值；JF 为节理特征系数，按表2.4.4 取值；RDI 为密度系数，RDI ＝25RD-50，RD 为密度，g／m3；HF 为硬度系数，当E＜50GPa时，HF＝E／3；当E＞50GPa 时，HF＝UCS／5，其中，E 为杨氏模量，GPa，UCS 为抗压强度，MPa。

表2.4.3　 RMD岩石性能系数(www.xing528.com)

表2.4.4　JF 节理特征系数

（2）关于X50计算公式的修正。Kuz Ram模型是从试验中总结出来，比较适用于矿山开采爆破的块度分布模型，矿山开采石料大块粒径一般都在1.0m以上，而水电站面板堆石坝级配料开采中的ⅢA、ⅢB料的允许最大粒径一般分别限制在0.3m和0.6～0.8m，长江科学院在天生桥水电站面板堆石坝级配料开采中，发现用Kuz Ram模型X50计算公式计算ⅢB料时，结果与实际较接近，预报值较实际值大11.8%～37.7%；用于计算ⅢA料时，相对误差达150%左右。考虑到爆破石料最大粒径是诸多因素综合作用的结果，因此引入石料允许最大粒径Xm这一参数来描述其他未考虑因素对平均块度的综合影响，亦即引入参数Xm对X50计算公式进行修正。

根据天生桥ⅢA、ⅢB料试验数据和鲁布革、龙滩及西北口等工地的试验资料得到修正后的X50计算公式为：

现有研究表明，台阶爆破的抵抗线与其他爆破参数有密切关系；而抵抗线的大小依赖于钻孔与药包直径的大小，常用抵抗线与钻孔直径之比（W／d）、孔距与抵抗线之比（m＝a／W）、钻孔深度与抵抗线之比（h／W）、堵塞长度与抵抗线之比（Ld／W）、单位耗药量与岩石系数之比（q／A）等参数来处理。国外的试验研究表明，当d、A 确定之后，用a／W、h／W、Ld／W、q／A等探讨岩石破碎、抛掷等是有现实意义的。其中a／W 和h／W 对块度分布的影响在Kum-Ram模型中都有不同程度的反映；q／A 则直接反映在X50计算公式中；只有Ld／W 的影响没有在模型中反映出来，堵塞长度对爆破块度的影响较大，在一定程度上能够反映堵塞长度Ld对石料级配的影响，且在整个试验中抵抗线是不变的，即反映了Ld／W 对n 的影响。经对试验成果的分析计算，得出修正后n值计算公式为：

式中：Ld为孔口堵塞长度，m；L 为不计超深部分的装药长度，m；H 为台阶高度，m；其余符号意义同前。

（4）修正后的爆破块度分布模型的完整形式。长江科学院在天生桥级配料开采试验研究的基础上，提出的爆破块度分布模型的完整形式如下：

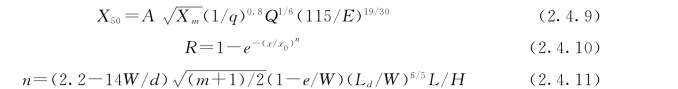
式中符号意义同前。

该模型主要适用于堵长比Ld／W 在0.68～0.72，原Kuz Ram模型限定n值在0.8～2.2，而该模型的n值多在0.8以下，可以将修正模型看作原模型在堆石坝级配料开采领域的拓展和延伸。