光的波粒二象性-《大学物理》

光在干涉、衍射、偏振等实验中，明显地表现出了波动性。然而在另一些实验中却体现出粒子性。例如，在黑体辐射实验中（所谓黑体就是吸收系数为1的物体），测得黑体的辐射能随波长的分布关系为图10—1所示的实线。但按经典的电磁学和统计物理学理论所得到的能量分布公式（Rayleigh—Jeans公式），其函数关系如图10—1中的虚线所示，它在波长λ→0时，是发散的，与实验完全不相符合。又例如在光电效应实验中，如果将光看成电磁波，就不能解释光电效应实验的一些实验规律。只有用光的量子理论才能很好说明这些实验现象。下面简要介绍一下上述这两个实验的一些基本规律、经典理论的缺陷及解决它的量子理论。

1.黑体辐射实验及其基本规律

在黑体辐射实验中，在某温度T下，测得黑体的辐射能随波长的分布关系如图10—1中的实线所示。图中的ε（λ，T）代表单位时间内，从物体单位面积上，在单位波长间隔中，向空间各个方向所发射的电磁波能量。因此，在单位时间内从物体单位面积上向各个方向所发射的波长在λ至λ+dλ范围内的辐射能量dΦ与dλ和温度T有关，当dλ取得足够小时，可认为dΦ与dλ成正比，即

若要计算所有波长范围的辐射能量，可用式（10—1）对波长积分，即

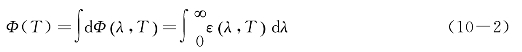
我们称Φ（T）为辐射通量，其单位为：瓦/米2（W·m-2）。

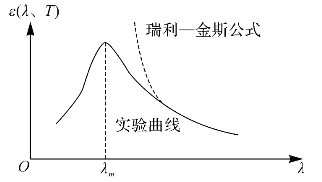
图10—1　黑体辐射的能量分布曲线

通过黑体辐射实验，总结出了如下一些基本规律：

（1）当曲线在λ→0和λ→∞时，都趋向于零，在中间某一波长λm处，辐射能量有一极大值；

（2）λm与T的乘积等于恒量，随辐射体温度的升高，辐射功率最大值所对应的波长向短波方向移动。这一规律可以用公式表示成

其中，b=2.898×10-3（m·K）；这一规律称之为维恩位移定律，利用它可以估计黑体的温度。

（3）黑体的总辐射通量Φ（T）与温度的四次方成正比，即

其中，σ=5.67×10-8（W·m-2·T-4）叫作斯特藩常量，称这一实验规律为斯特藩四次方定律。

以上是黑体辐射的基本实验规律，但瑞利根据经典电动力学和统计物理理论，得到的结果是；即当A→0时，ε（λ）是发散的。这就说明经典理论存在有缺陷，它不能很好地解释黑体辐射实验，从而暴露出经典理论的局限性。

为了解决经典理论的这一缺陷，德国著名的物理学家，普朗克（M.Planck）于1900年发表了关于黑体辐射的能量子假说。他指出：

①黑体由带电的线性谐振子组成，这些谐振子所具有的能量不连续变化，只能取一些分立值：ε，2ε，3ε……其中ε=hv为谐振子所具有的最小能量，h为普朗克常量，h=6.63×10-34（J·s）；v为谐振子的振动频率。

②这些谐振子在辐射和吸收过程中，其辐射能和吸收能只能取这一最小能量的整数倍。(www.xing528.com)

我们称这些谐振子所具有的能量以及它们所发射的能量是量子化的。

在普朗克假说的基础上，再用经典理论，即可得到著名的普朗克公式

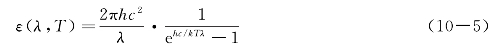
根据式（10—5）求极大值即可得到维恩位移定律；将式（10—5）对波长积分可得到斯特藩四次方定律。它与实验曲线完全相符，但普朗克的量子假说却是经典理论所无法解释的。

2.光电效应实验

另一个重要的实验是光电效应实验。它是在1887年由德国物理学家赫兹（H.R.Hertz），在验证电磁波的存在时首次发现的，在光电效应实验中，有一些规律是光的波动理论所无法解释的，这些规律主要有以下几条。

（1）实验中存在一“截止频率”v0，当入射光频率低于这一频率时，无论入射光的强度如何，都不能发生光电效应。

（2）光电效应中的反向遏止电压与入射光的频率间存在一线性关系，与入射光强度无关，即v0=kv-A0；其中k和A0为两个实验常量，v为入射光频率。

（3）当入射光照射到金属上，立即有光电效应产生，弛豫时间极短。

为了解决经典理论的这一缺陷，德国的物理学家爱因斯坦（A.Einstein）在1905年提出了光量子假说。

（1）光束是由光粒子流组成，这些粒子被称之为光子；

（2）光子所具有的能量为

其中，h为普朗克常量，v为光的频率。爱因斯坦在同年提出的相对论中给出了光子的动量

（3）光在被吸收和发射光程中，能量是量子化的。

按照爱因斯坦的理论，电子在吸收光能时，每次只能吸收一个“完整”的光子，所得到的能量为hv，一部分用来克服金属的逸出功A，另一部分则转化为电子的初动能。从而得到了著名的爱因斯坦方程

方程中的A为金属的逸出功；为电子的初动能。根据爱因斯坦的光子假说，电子初动能的大小就是反向遏止电压的反映，即；所以反向遏止电压仅决定于入射光的频率，与入射光的强度无关。另外，当hv≤A时，将不能产生光电效应。对应的“截止频率”v0为v0=A/h；因此，根据爱因斯坦的光子假说，可以圆满地解释光电效应实验，从而确立了光的量子性。由此可见光不仅具有波动的性质，而且还具有粒子性。光的这种波动性与粒子性并存的性质，称为光的波粒二象性。