熵的概念及其在热力学中的应用

根据卡诺定理，一切可逆热机的效率都可以表示为

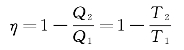
由此式可以得到

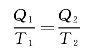
或者写为

式中，Q1是工作物质从温度为T1的高温热源吸收的热量；Q2是工作物质向温度为T2的低温热源释放的热量。

根据热力学第一定律对热量符号的规定，当系统放热时，此热量应以负值表示，所以Q2应以-Q2代替，于是式（9—26）成为

这是在一次可逆卡诺循环中必须遵循的规律。

一个任意的可逆循环ACBDA，总可以用大量微小的可逆卡诺循环代替，如图9—11所示。而对于其中的每一个卡诺循环，都可以列出相应于式（9—27）的关系式，将所有这样的关系式叠加起来，就得到

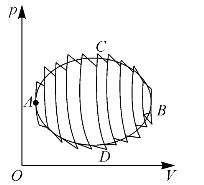
图9—11　任意可逆循环可看作由无限多个卡诺循环组成

当无限缩小每一个小循环时，上式中的Qi可用δQ代替，求和号可用沿环路ACBDA的积分代替，于是上式可以写为

(www.xing528.com)

此式称为克劳修斯等式。对于任意可逆循环，克劳修斯等式都成立。

在图9—11中，可以将点A看作初状态，将点B看作末状态，由初状态A到达末状态B可以沿过程ACB进行，也可以沿过程ADB进行。根据式（9—28），应有

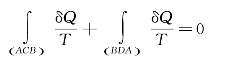
可以改写为

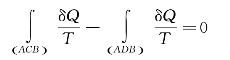
即

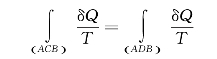
上式表示，沿不同路径从初状态A到末状态B，δQ/T的积分值都相等。或者说，δQ/T的积分值只决定于初、末状态，而与过程无关。可见，δQ/T的积分值必定是一个状态函数，这个状态函数就称为熵，常用S表示。从初态A到末态B，熵的变化可以表示为

对于无限小的过程可以写为

上式给出在无限小可逆过程中，系统的熵变dS与其温度T和系统在该过程中吸收的热量δQ的关系。

熵是状态函数，完全由状态所决定，也就是完全由描述状态的状态参量所决定，所以确定了只要系统所处的平衡态，也就完全确定这个系统的熵，而与通过什么过程到达这个平衡态无关。在由式（9—29）计算的熵值中总包含了一个任意常量，这可以从式（9—29）的积分式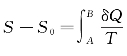或者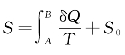中看到，式中S0就是这个任意常量。这与力学中求势能的情形相似，力学中为了消除或确定这个包含在势能中的常量，总是要选择势能零点。在这里，为了消除或确定包含在熵值中的常量也需要选择熵值为零或为某定值的参考态。

既然状态函数熵完全由状态所决定，那么从初状态A到末状态B 熵变（SB-SA），就完全由A、B两个状态所决定，而与从初状态到末状态经历怎样的过程无关。但是要计算熵变（SB-SA），却必须沿一条可逆过程从A到B对δQ/T积分，也就是说，在由式（9—29）计算熵变时，积分路径代表连接初、末两状态的任意可逆过程。所以在计算熵变时，总是在初、末两状态之间设计一个可逆过程，或者在p—V图中找寻一条便于积分的路径，或者计算出熵作为状态参量的函数关系，再代入初、末两状态的状态参量。