《大学物理》：气体内的输运现象探究

关于气体内分子碰撞的统计规律是在气体处于平衡态的条件下得到的。不过，对于与平衡态偏离不是太大的非平衡状态，也可以借助上面导出的结果进行分析。

若气体处在非平衡状态，气体内各部分物理性质（如密度、流速或温度）是不均匀的。由于气体分子做热运动和不断互相碰撞，气体内各部分将由不均匀而逐渐趋于均匀一致。在此过程中，至少有一个物理量（动量、质量或能量）在气体内由一处输运（迁移）到另一处，因此，这样的过程称为气体内的输运过程（也称内迁移过程）。气体内的输运现象基本上有以下三种。

1.黏滞现象

黏滞现象也称为内摩擦现象，是由于气体内气层之间速度的不均匀性引起的，被输运的是动量。在做相对运动的两层流体之间的接触面上，将产生一对阻碍两层流体相对运动的、大小相等而方向相反的黏力作用，如图8—14所示，其大小为

式中，η是流体的黏度，流体沿y方向做定向流动，并且流动速率沿z方向递增；流体定向流动速率梯度在z0处之值是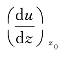；△S是在z0处两流体层接触面的面积。

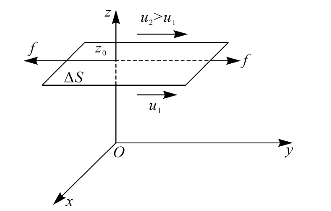
图8—14　气体中各气层的流动速率的不同

将式（8—24）所反映的宏观规律应用于现在讨论的气体系统中。从气体动理论观点来看：系统中每个分子除具有热运动的动量外，还具有定向运动的动量。设分子的质量为m，则分子定向运动的动量为mu。在接触面ΔS下侧的气体层中的分子，定向运动的速度为u1，定向运动的动量为mu1。在接触面ΔS上侧的气体层中的分子，定向运动的速度为u2，定向运动的动量为mu2，并且mu2＞mu1，如图8—15所示。由于热运动，下气层中的分子携带较小的定向运动动量mu2，通过接触面ΔS迁移到上气层中。又由于分子间的碰撞，定向运动动量被均匀化，所以上气层中定向运动动量减小。与此同时，上气层中的分子携带较大的定向运动动量mu2，通过接触面ΔS迁移到下气层中，使下气层中定向运动动量增大。这种分子定向运动动量均匀化的过程，在宏观上就表现为两气层之间相互作用的黏力。所以，黏性现象是气体分子定向运动动量输运的宏观表现。

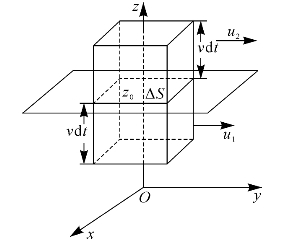
图8—15　导出气体层之间的黏力公式示意图

下面先讨论导出时间内两气层通过ΔS面交换的分子数，再讨论分子穿越ΔS所输运的定向运动动量。

在接触面ΔS上侧的气层中，导出时间内能够穿越ΔS面到达下侧气层的分子数，如图8—15所示的以ΔS为底、以为高的柱体内的一部分分子。如果系统内单位体积的分子数为n，设想一个单位体积内的n个分子，由于热运动，在导出时间内全部离去，与此同时，相同数目的分子由该立方体以外的空间进入该立方体。这个立方体的6个面中的任何一个，都不比其他面特殊，所以通过单位立方体的任何一个面进入或离去的分子数都是n/6。于是，在导出时间内，穿越ΔS面由上侧气层到达下侧气层的分子数应为

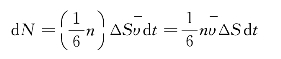
同理，在dt时间内，穿越ΔS面由下侧气层到达上侧气层的分子数，也必定等于dN。

分子的交换引起定向运动动量的迁移，上、下气层通过接触面ΔS所迁移的定向运动动量的大小为

因为气体定向流动的速率沿z方向递增，所以，实际上dp是沿z轴的负方向由上侧气层通过ΔS面输运到下气层的定向运动动量，应该写为

处于ΔS面下侧气层中将要交换的分子，在穿越ΔS面以前最后一次碰撞的位置上定向运动速率为u1，那么最后一次被碰撞的位置应该在何处？显然，对于每一个即将穿越ΔS面的分子来说，所处位置是不同的，但不管怎样不同，通过最后一次碰撞它们都一定穿越ΔS面到达上气层中。所以平均地说，可以认为它们是处于ΔS面以下并与ΔS面相距一个平均自由程的位置，即处于处。在ΔS面上侧气层中将要交换的分子，穿越ΔS面以前最后一次碰撞的位置上定向运动速率为u2，同样可以认为这些分子是处于ΔS面以上，并与ΔS面相距一个平均自由程的位置，即处于处，所以

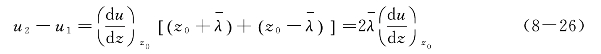
将式（8—26）代入式（8—25），得

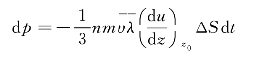
以ΔS相隔的两层气体层之间的黏力为

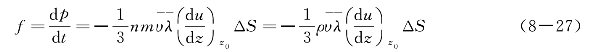(www.xing528.com)

式中，ρ是气体的密度，ρ=nm。

将式（8—24）与式（8—27）相比较，可以得到气体的黏度η与分子微观量平均值之间的关系

式（8—28）表示，气体的黏度η取决于系统中单位体积的分子数n、分子的质量m、分子热运动的平均速率和平均自由程，而这些量都是由气体自身性质和所处状态决定的。

决定气体黏度η的三个量（ρ、和），其中平均速率与气体的压强无关，密度ρ与气体的压强成正比，分子的平均自由程与压强成反比。于是，由式（8—28）可以得到气体的黏度与压强无关的结论。对于这个结论，解释如下：虽然随着系统压强的降低，单位体积内的分子数将减少，穿越ΔS面交换的分子对数将减少，但由于分子的平均自由程随压强的降低而增大，距离ΔS面更远的分子也能穿越ΔS面而参与交换，致使参与交换的分子所携带的定向运动动量增大，所以参与交换的分子所迁移的总的定向运动动量仍能保持不变，故黏度与压强无关，这个结论也得到实验的证实。表8—1列出了在不同压强下测得的二氧化碳气体的黏度值。

表8—1　在不同压强下测得的二氧化碳气体的黏度值

由表8—1中的数据可见，二氧化碳气体的黏度在很宽的压强范围内都保持恒定，仅当压强很低时才表现出变化的趋势：在极低压强下，气体的黏度不再是恒定的，而是与压强成正比。这是因为在极低压强下分子的平均自由程变化很大，当等于或大于容器的线度时，分子的实际自由程被容器壁所限定，可以认为分子的平均自由程的最大值就是容器的线度。此时这三个决定气体黏度η的量（ρ和）中只有ρ与压强成正比，所以，在极低压强下，气体黏度η与压强成正比。由于ρ和与温度无关，而与热力学温度的平方根成正比，所以气体的黏度η与成正比。这正是指出的气体黏度随温度升高而增大的原因。

2.热传导现象

热传导现象是由于气体内各处温度的不均匀性而引起的，被输运的是能量。

当气体系统中温度不均匀时，热量将会从高温处传到低温处，这就是热传导过程。假设温度沿z方向逐渐升高，即沿z方向存在温度梯度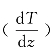。在z0处取一截面ΔS垂直于z轴，热量将通过ΔS面从上部传到下部，如图8—16中箭头所示。

若以dQ表示在dt时间内通过ΔS面沿z轴正方向传递的热量，则存在下面的宏观规律

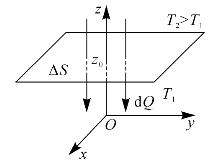
图8—16　导出热传导公式示意图

式中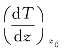，表示在z0处的温度梯度；比例系数κ称为气体的热导率，它决定于气体的性质和所处的状态；式中负号（-）表示热量沿温度降低的方向传递，即沿z轴负方向传递，如图8—16中箭头所示。

从气体动理论观点来看，温度的高低就是分子热运动平均动能的大小，热传导过程是分子热运动平均动能输运的宏观表现。可以用与黏性现象相似的方法分析热传导过程，并得到气体的热导率κ与微观量平均值等之间的关系

式中，cv是气体系统在等体过程中的比热。

式（8—30）表明，气体的热导率取决于系统中单位体积的分子数n、分子质量m、分子平均速率、平均自由程以及气体的定体比热cv。

比较式（8—29）和式（8—30），可得

κ=ηcv

因为cv只决定于气体分子自身的性质，是常量，所以κ的基本性质与η类似。在通常压强下，κ也应与压强无关，而在极低压强下，κ与压强成正比。杜瓦瓶（生活中常用的热水瓶是杜瓦瓶的一种）就是根据热导率κ的这种性质制成的，它是一种双层薄壁的玻璃容器，夹层间空气被抽得很稀薄，当达到上述极低压强的范围时，热导率随夹层中气压的降低而减小，从而达到绝热的目的。κ与温度的关系也和η与温度的关系相同，即与η成正比。

在国际单位制中，热导率的单位是W·m-1·K-1［瓦/（米·开）］。